Biological and Environmental Effects of Server Sky

Thinsats may stay in orbit a long time - perhaps thousands of years. We cannot assume they will always be under beneficent control, and need to include the worst case in our design.

The extreme case is biological doomsday. For an information system, that could be as simple as providing very bad information to credulous and lethally-armed surface-dwellers. But as Justice Brandeis once said, the cure for bad speech is more speech. As long as there are many channels of information, independently controlled, Server Sky merely increases the bandwidth, and intelligent people will hesitate before launching Armageddon. Anxious people will still be anxious, and some may choose to redirect their anxieties at Server Sky. But that does not make it lethal.

Leaving aside the dangers (and anti-dangers) posed by information, the rest of this page will focus on the physical aspects of Server Sky, a collection of objects that have some mass and emit or reflect heat, light, and microwave radiation.

Mass risks

Thinsats are very thin - unless a cylinder of thinsats fails to deploy, or a cylinder is remade out of removed-from-service thinsats, they will be far too thin to survive reentry. Chances are, charging effects will push thinsats apart, so they will not tend to clump before they potentially reenter. When they do reenter, they will probably turn into flakes and sand.

The major risk posed by thinsat mass is collision with other space objects, perhaps some inhabited. If space objects have value, we will be active in space and managing the thinsats.

Heat risks

The constellation of thinsats will not be dense enough reflect or emit enough heat to be a problem in the foreseeable future. If thinsats (at 75C or about 350K ) are dense enough to be a significant infrared source (slightly heating the globe) then they will probably reflect far larger amounts of sunlight, which we will discuss in the next section.

Since the Earth is cooled by black body radiation, proportional to temperature to the 4th power, a 1% increase in incoming energy will cause only a 0.25% increase in absolute temperature. If an acceptable Earth temperature rise is only 0.1 Kelvins above the average black body temperature of 255K, the temperature rise is caused by 4E-4 of the solar input. Assuming the Earth is surrounded by a sparse shell of thinsats emitting collected solar radiation isotropically as thermal radiation, then the density of radiated energy is 25% of the incoming radiation. Working through the math, it turns out that the shell must capture 1.6E-3 of the sun's energy passing through the shell to re-radiate enough infrared in the direction of the Earth to heat it by 0.1K . That is a LOT of thinsats. Here is the number of 15 cm-solar-cell thinsats (0.02m²) at various distances that can capture 1.6E-3 of the sun's energy:

Earth Heating Limits (0.1K)

There are no near-term thermal limits to thinsat constellation size, assuming larger constellations can move further out.

Light Risks

The big problem with accidental light reflection is undesirable illumination of the dark night sky on Earth. With the thinsats intact, properly optically designed, and under good control, they will put very little light into the night sky. We don't want to deal with rampaging astronomers, do we? In the worst case, we may not be too worried about astronomers, but there are other reasons to keep the night sky dark.

Assume it is a long time from now, and the constellation contains many abandoned thinsats. In the very long term, Earth-orbiting thinsats will be oriented flat in the equatorial plane, edge-on to Earth, with only diffuse reflection during summer and winter. Before that, unless they are actively controlled, the thinsats may spend a long time tumbling in random orientations, and will reflect some light on the earth. Let's assume the intended black surfaces of the thinsats have been weathered by micrometeorites, and the average albedo is 0.5 on both sides.

The thinsats will be pointed in all directions. They will always intersect a plane perpendicular to the vector towards the sun. Let the line of intersection define an axis of rotation. The average light intercepted by the sun is the proportional to the average area, facing the sun, of a thinsat rotated around that axis, or the average area between 0 and 90 degrees rotation, or 2/\pi times the maximum area. For an average radius of B meters, the average area facing the sun and collecting sunlight is 2 B^2 .

This light from this area will be scattered over a mirror sphere, but unevenly. Imagine the light deposited onto a half sphere. The illumination normal to each surface element is the full illumination times the cosine of the angle of that surface from the sun. The integral of all the light scattered is 2 a I_s B^2 where I_s is the solar illumination of 140,000 lumens, and a is the albedo, assumed to be 0.5 for a heavily damaged surface (it starts out much lower). The light is reflected off that mirrored surface leaves at twice the angle. For a outbound angle of \beta , the illumination is equal to K cos( \theta / 2 ) . The solid angle increment as a function of \beta is 2 \pi sin( \beta / 2 ) d \beta , so the total illumination 2 a I_s B^2 is equal to the integral of 2 \pi K cos( \beta / 2 ) sin( \beta / 2 ) between 0 and \pi . The integral of the expression is \pi ^ 2 K . This results in K = 2 a I_s B^2 / \pi ^2 , and an illumination of I( \beta ) = ( 2 a I_s B^2 / \pi ^2 ) cos( \beta/2 ) per average tumbling thinsat.

Only some of the thinsats will be in the night sky of a given equatorial point, and only some of the thinsats will be outside the earth's shadow. The light delivered to the ground, per square meter, is the light per solid angle, divided by the distance { R_{se} } ^ 2 , and multiplied by the cosine of the angle of the arriving light from the zenith \alpha , for the visible and illuminated thinsats. This is difficult to integrate numerically, but it is fairly easy for a computer. For I_s = 100K lumen illumination (after atmospheric attenuation), and an albedo a = 0.5 , the total light delivered to an equatorial spot by 80 billion thinsats can be computed by this C program and fed to gnuplot with this control file to get this graph: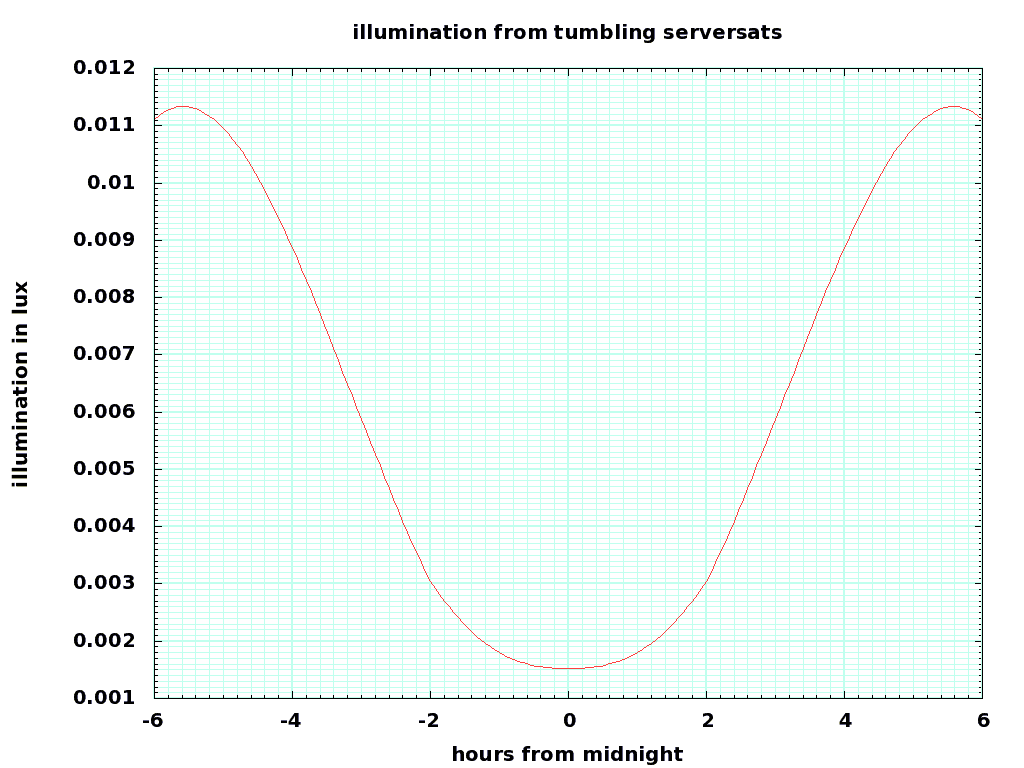

The illumination peaks half an hour after dusk and before dawn, at about 0.01 lux, then drops to 0.002 lux around midnight. This graph applies at the spring and fall equinoxes, and will be somewhat different at the summer and winter solstices. Note that this also does not include the increased atmospheric attenuation of light coming in diagonally, so the actual measurements will be smaller than the graph. This needs a better calculation.

Corals

MoreLater

Corals may be triggered to incorrectly spawn with as little as 10% of full moon illumination (which is 1E-5 full sun), or 1E-6 of full sun illumination in the night sky. This would be the illumination from 1000 billion thinsats at M288 near dawn and dusk. Assuming this threshold (it might be quite a bit higher, and needs to be characterized empirically with real corals), 80 billion thinsats will offer a safety factor of at least 10.

Night Illumination

This is much lower than the thermal limit. If each thinsat, configured as a power-sat, could deliver 1 watt each to the electric grid, then "Power Sky" could deliver only 850 gigawatts from GEO distances. To provide 50 Terawatts ( the Smalley Terawatt challenge for 2100 ) we will have to go out to the moon.

Note that this same limit applies to any other kind of space solar power system with the same efficiencies Space solar power systems may need to be at lunar distances to provide large amounts of power in normal operation, while avoiding the "coral problem" after failure.

MoreLater

Microwave risks

Unlike the risks above, the microwave risks are worst during improperly controlled "normal" operation; hijacked arrays used as microwave beam weapons. In normal conditions, communication arrays are providing enough energy to move bits. With a 17dB carrier to noise ratio (quite high!) and a noise temperature of 50K, each bit uses 50kT or 3.5E-20 joules. A 10 Gbps signal captured by a 1m² antenna array equates to a power density of 3.5E-10 W/m² . If there are 1000 such signals impinging on any particular area of the surface at once (spatially and frequency and code multiplexed) then the power level is 0.25 microwatts per square meter - no discernable biological effect.

Power beams will be a different story. Although some SSPS proposals posit a low energy density and a large rectenna, they are merely spreading out the problem in hopes of staying below some small average "safe" dose. This is not a practical use of surface area, if the goal is to produce a 50 terawatts of power globally. It may be better to focus the beam down onto a number of 10km diameter rectennas at very high power densities, perhaps 10 KW/m² peak. Assuming 50% utilization and 80% collection efficiency, that translates to 12500 km² of rectennas, or 160 of these 10km diameter arrays scattered around the globe.

However,larger areas nearby will be subject to sidelobe radiation, and rectennas will probably be surrounded with a kilometer of "no fly zone". When birds enter, they are scared away. If they get too close, the beam is turned off. Turnoff takes about 3 seconds, given the speed of light delay to and from lunar distances.

A few kilometers around the array may be covered with wire mesh, with low plants growing underneath, like at the Arecibo radio observatory. Farther out, the sidelobe microwave power will still exceed radiation guidelines for unshielded people, but people in vehicles or wearing protective clothing will do fine. The land can be used for agriculture, or as wildlife preserves. The abundance of life in the exclusion zones around Chernobyl demonstrate that wild nature thrives in radiation zones that scare away humans. Again, the beams can be turned off while people are in the unshielded sidelobe areas.

So an entire "rectenna reservation" may be 50km across, for a total area of 320000 km². The land surface of the Earth is 149 million km², so the land usage is 0.2% of the total land surface. Much smaller than high efficiency PV solar arrays, and vastly smaller than biofuel crop arrays. Most of the reservation area will be useful for life, if not inhabited, unlike solar arrays.

MoreLater

Question : how much power is needed to vaporize clouds, or blow them away with the heat column rising from a hot rectenna?

MoreLater

Weaponized microwave power beams

Transmitters with focuses capable of sharp power dropoff at the edge of the rectenna will be able to form spot beams as sharp as the dropoff. Potentially all the power-sat arrays facing a particular small area on earth will be able to dump all their beam power into a sharp spot. If 25 Terawatts is focused on 5 square kilometers, the beam power is 5 Megawatts per square meter, or 5000 suns, or 1 kiloton of nuclear weapon equivalent per second per square kilometer. This would vaporize people and torch cities.

This cannot be allowed to happen, of course. There are many system controls that can be added, from the political down to the operational. Perhaps the best way to protect cities from such treatment is to make the transmitters respond only to ground guide beams, perhaps beaming up "E-cash" messages to buy the power from the array. Otherwise, the arrays do not get proper phasing information and cannot focus.

At 2.8 cents per kilowatt hour, or 1 cent per megajoule, it would cost 250 thousand dollars per second to pay for a 25 TW beam (and probably lots more to outbid all the other arrays competing for the same power). Chances are, the source of the guide beam will get blown out or scrambled by all the incoming power, so the burst would be uncomfortable, but brief. So even if all the interlocks fail, economics could save the day.

Actually, if the E-cash messages are cryptographically signed with receiver location information and time, then there are more defenses still; don't issue E-cash for weaponized use.

Another protection for cities might involve "scrambling" beams. The transmitter hardware can be designed to decohere when focus is attempted on a scrambler. While this may lead to sabotage and denials of service, if designed into the hardware it will be very difficult to get around.

Obviously, before we get to power levels that can do this level of harm, we will need to design many levels of defense in depth, relying on design and physics to protect us. And before these systems are turned on, we must insist that the designs are open and inspectable, and the thinsats coming off the manufacturing lines adhere to the safe designs, before we permit them to be launched.

MoreLater