|
Size: 199
Comment:
|
Size: 3178
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| #format jsmath | |
| Line 3: | Line 4: |
=== 60K 50AU Dyson shell === $ \Large B(\lambda) = \LARGE { { 2 h c } \over { \lambda^3 \left( e^{ h c / \lambda k T } - 1 \right) } } = { { 4e19 ~ Jy / sr ~ {\mu}m^3 } \over { \lambda^3 \left( e^{ 240 {\mu} m / \lambda } - 1 \right) } } $ This is for an infinite resolution imager - at large distances, the power is the image angular area divided by the pixel angular area. This scales the intensity way down for distant Dyson shells. If the ratio of shell intensity to background is $ F $, the pixel size in arcseconds is $ px $, the shell radius in AU is $ r $, and the distance in parsecs is $ R $, then the angular size $ A $ is: $ A ~ = ~ \pi ( r / R )^2 $ $ F ~ = ~ px^2 / A = ( px ~ R / r ) ^2 / \pi $ $ R ~ = ~ ( 50" / px ) \sqrt{ \pi F } $ $px$ is 90" (90 arcseconds) for IRAS, 12" for WISE, and .11" for JWST. It is 2.3" for Spitzer MIPS ('''M'''ultiband '''I'''maging '''P'''hotometer for '''S'''pitzer) 24 μm (128x128 pixels) and 9.4" for Spitzer 70 μm (16x32 pixels). $ R ~=~ 0.96 \sqrt{ F } $ for IRAS, $ 7.2 \sqrt{ F } $ for WISE, and $ 790 \sqrt{ F } $ for JWST. Of those three, only IRAS has sensors for wavelengths longer than 25 μm. $ R ~=~ 38 \sqrt{ F } $ for 24 μm Spitzer and $ 9.2 \sqrt{ F } $ for 70 μm Spitzer. ----- |
|
| Line 5: | Line 25: |
| from http://lambda.gsfc.nasa.gov/product/cobe/cobe_image_table.cfm | WHAT IS THE SCALE??? from http://lambda.gsfc.nasa.gov/product/cobe/cobe_image_table.cfm The zodiac is highly inclined compared to the galaxy, but these plots show it intersecting near galactic center. This is fortunate if true - we are unlikly to distinguish a Dyson shell where the background is very dense (too confusing) or very thin (radially outwards, fewer candidates). [[attachment:Ellisfig58b.jpg | {{attachment:Ellisfig58b.jpg | | width=512}}]] . frequency = 299792 GHz-μm/λ . Ellis: Z zodiacal, C cirrus . B 60K 100 AU 1-sun Dyson, full pixel || Band(um) || 12μm || 25μm || 60μm || 70 μm || 100μm || || frequency || 25 THz || 12 THz || 5 THz || 4.3 THz || 3 THz || || Z nW/m^2^-sr || 2800 || 1800 || 190 || 130 || 42 || || Z Jy-sr || 1.12e7 || 1.5e7 || 3.8e6 || 3.0e6 || 1.4e6 || || C nW/m^2^-sr || 4.8 || 2.3 || 3.2 || 4.5 || 13 || || C Jy-sr || 1.9e4 || 1.9e4 || 6.4e4 || 1.1e5 || 4.3e5 || || B Jy-sr || 4.8e7 || 1.7e11 || 3.5e12 || 3.9e12 || 4.0e12 || || B/(C+Z) || 4.3 || 1.1e4 || 9.1e5 || 1.3e6 || 2.2e6 || we will probably ignore zodiacal measurements || || F=B/C || 2.5e3 || 8.9e6 || 5.5e7 || 3.5e7 || 9.3e6 || assume measurements in galactic plane || || R IRAS pc || 49 || 2900 || 7000 || -- || 3000 || || R WISE pc || 135 || 8000 || -- || -- || -- || || R Spitzer pc || -- || 110000 || -- || 54000 || -- || || R JWST pc || 1400 || 84000 || -- || -- || -- || |
Galactic Cirrus and Zodiacal Light
60K 50AU Dyson shell
\Large B(\lambda) = \LARGE { { 2 h c } \over { \lambda^3 \left( e^{ h c / \lambda k T } - 1 \right) } } = { { 4e19 ~ Jy / sr ~ {\mu}m^3 } \over { \lambda^3 \left( e^{ 240 {\mu} m / \lambda } - 1 \right) } }
This is for an infinite resolution imager - at large distances, the power is the image angular area divided by the pixel angular area. This scales the intensity way down for distant Dyson shells. If the ratio of shell intensity to background is F , the pixel size in arcseconds is px , the shell radius in AU is r , and the distance in parsecs is R , then the angular size A is:
A ~ = ~ \pi ( r / R )^2
F ~ = ~ px^2 / A = ( px ~ R / r ) ^2 / \pi
R ~ = ~ ( 50" / px ) \sqrt{ \pi F }
px is 90" (90 arcseconds) for IRAS, 12" for WISE, and .11" for JWST. It is 2.3" for Spitzer MIPS (Multiband Imaging Photometer for Spitzer) 24 μm (128x128 pixels) and 9.4" for Spitzer 70 μm (16x32 pixels).
R ~=~ 0.96 \sqrt{ F } for IRAS, 7.2 \sqrt{ F } for WISE, and 790 \sqrt{ F } for JWST. Of those three, only IRAS has sensors for wavelengths longer than 25 μm. R ~=~ 38 \sqrt{ F } for 24 μm Spitzer and 9.2 \sqrt{ F } for 70 μm Spitzer.
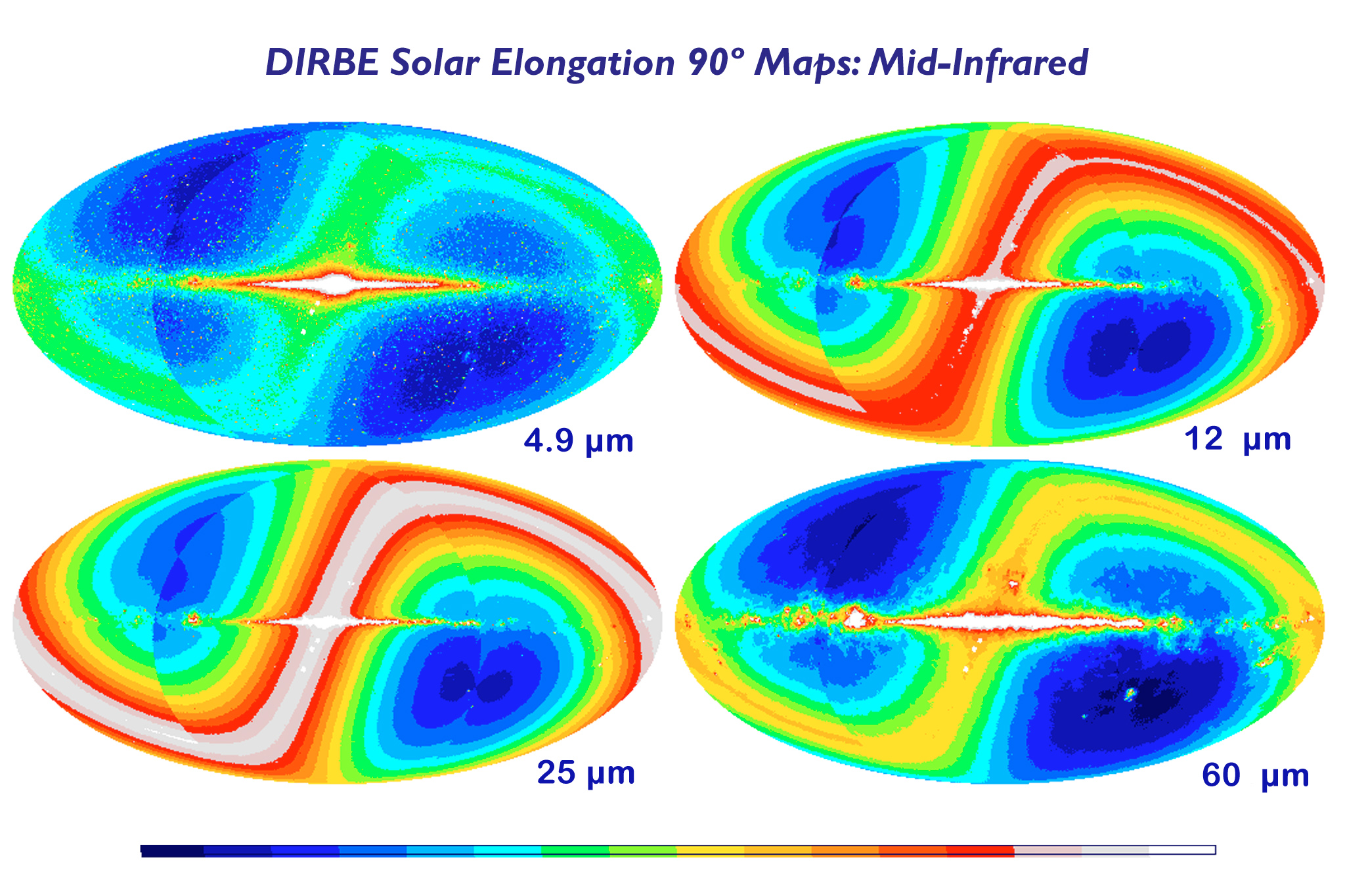
WHAT IS THE SCALE??? from http://lambda.gsfc.nasa.gov/product/cobe/cobe_image_table.cfm
The zodiac is highly inclined compared to the galaxy, but these plots show it intersecting near galactic center. This is fortunate if true - we are unlikly to distinguish a Dyson shell where the background is very dense (too confusing) or very thin (radially outwards, fewer candidates).
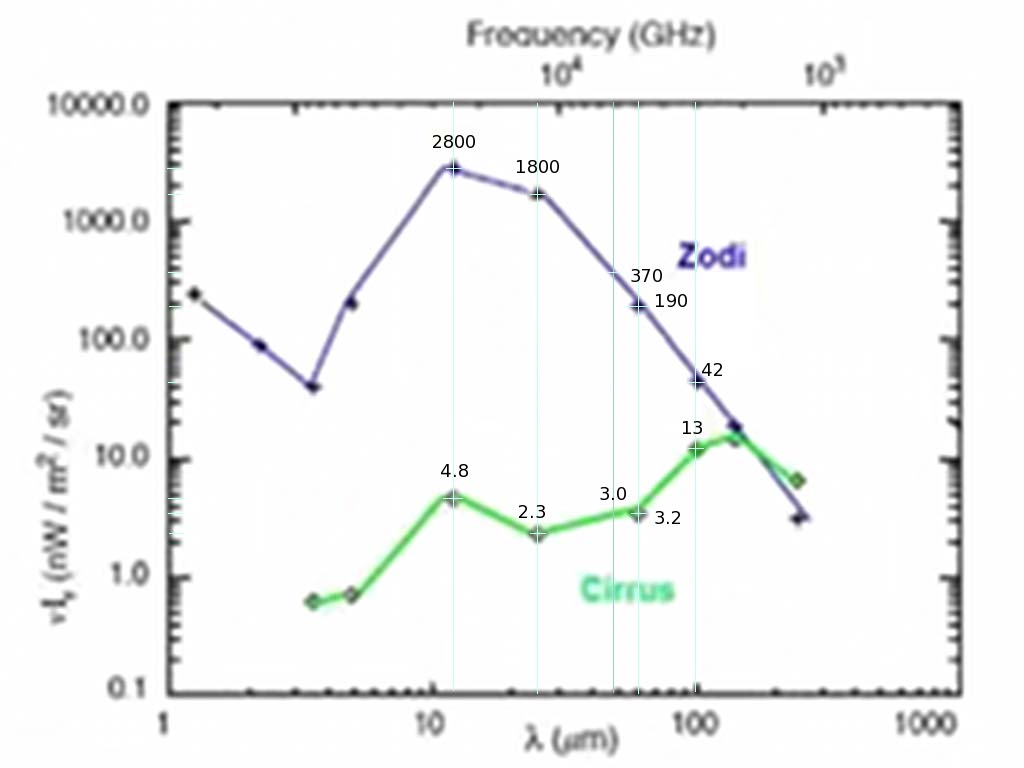
frequency = 299792 GHz-μm/λ
- Ellis: Z zodiacal, C cirrus
- B 60K 100 AU 1-sun Dyson, full pixel
Band(um) |
12μm |
25μm |
60μm |
70 μm |
100μm |
|
frequency |
25 THz |
12 THz |
5 THz |
4.3 THz |
3 THz |
|
Z nW/m2-sr |
2800 |
1800 |
190 |
130 |
42 |
|
Z Jy-sr |
1.12e7 |
1.5e7 |
3.8e6 |
3.0e6 |
1.4e6 |
|
C nW/m2-sr |
4.8 |
2.3 |
3.2 |
4.5 |
13 |
|
C Jy-sr |
1.9e4 |
1.9e4 |
6.4e4 |
1.1e5 |
4.3e5 |
|
B Jy-sr |
4.8e7 |
1.7e11 |
3.5e12 |
3.9e12 |
4.0e12 |
|
B/(C+Z) |
4.3 |
1.1e4 |
9.1e5 |
1.3e6 |
2.2e6 |
we will probably ignore zodiacal measurements |
F=B/C |
2.5e3 |
8.9e6 |
5.5e7 |
3.5e7 |
9.3e6 |
assume measurements in galactic plane |
R IRAS pc |
49 |
2900 |
7000 |
-- |
3000 |
|
R WISE pc |
135 |
8000 |
-- |
-- |
-- |
|
R Spitzer pc |
-- |
110000 |
-- |
54000 |
-- |
|
R JWST pc |
1400 |
84000 |
-- |
-- |
-- |