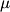Cold Dark Matter

New Scientist 2017 11 October

• https://www.newscientist.com/article/mg23631472-000-half-the-universes-missing-matter-has-just-been-finally-found/

Hideki Tanimura at the Institute of Space Astrophysics in Orsay, France

• A Search for Warm/Hot Gas Filaments Between Pairs of SDSS Luminous Red Galaxies

• Detection of intercluster gas in superclusters using the thermal Sunyaev-Zel'dovich effect

Anna de Graaff at the University of Edinburgh, UK.

• Missing baryons in the cosmic web revealed by the Sunyaev-Zel'dovich effect

There may be no exotic dark matter, just gas that is very difficult to detect without large, sensitive instruments in space. Planck can only image some of this "dim" matter by overlaying hundreds of images, which cannot detect other baryons (mostly protons) that are not clustered this way.

Rotation Curves around a Line Mass

"Heavy" line mass filaments perpendicular to a galaxy produce rotation curves with constant velocity at any radius.

da ~=~ gravity \times cos( angle )

da ~=~ \Large { { \mu \lambda dy } \over { l^2 } } { r \over l }

a ~=~ \mu \lambda r \Large \int_{-\infty}^{+\infty} { dy \over l^3 }

substitute y = b r :

dy ~=~ r ~ db

l ~=~ \sqrt{ r^2 + y^2 } = \sqrt{ r^2 + b^2 r^2 } = r \sqrt{ 1 + b^2 }

a ~=~ \mu \lambda r \Large \int_{-\infty}^{+\infty} { r db \over { r^3 ( 1 + b^2 )^{3/2} } }

a ~=~ \Large { { \mu \lambda } \over r } \int_{-\infty}^{+\infty} { db \over { ( 1 + b^2 )^{3/2} } }

a ~=~ \Large { { 2 \mu \lambda } \over r }

For circular orbital motion, ~ a ~=~ v^2 / r ~ , so v^2 ~ = ~ 2 \mu \lambda

Therefore, for an infinite line mass, rotation velocity is constant, regardless of radius.

And this matches galactic rotation curves, for example: