|
Size: 2376
Comment:
|
Size: 2380
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 10: | Line 10: |
| If the displacement of the unconstrained orbit differs from the equatorial orbit by $ d = D \sin{ \omega t } $, then the acceleration is $ a = - \omega^2 D \sin{ \omega t } $. Since $ \omega^2 = \mu / R^3 $ for a circular orbit without the $ J_2 $ perturbation, the peak acceleration is \mu D / R^3 . For μ = 398600.44 km^3^/s^2^, the acceleration at maximum displacement is given for various altitudes in the table below, as well as the accumulated $ \Delta V $ over a 10 year mission: | If the displacement of the unconstrained orbit differs from the equatorial orbit by $ d = D \sin{ \omega t } $, then the acceleration is $ a = - \omega^2 D \sin{ \omega t } $. Since $ \omega^2 = \mu / R^3 $ for a circular orbit without the $ J_2 $ perturbation, the peak acceleration is $ \mu D / R^3 $ . For μ = 398600.44 km^3^/s^2^, the acceleration at maximum displacement is given for various altitudes in the table below, as well as the accumulated $ \Delta V $ over a 10 year mission: |
| Line 12: | Line 12: |
| ||<-2> ||<-2> per meter of displacement D || | |
| Line 13: | Line 14: |
| || || || per meter D || per meter D || |
Displacement and Acceleration
Arrays of satellites cannot maintain a constant displacement above or below the orbital plane without a constant (and significant) acceleration keeping them there. The ΔV needed over the lifetime of a satellite is beyond the range of high Isp engines. Further, it is unnecessary; by using constellations that evolve and rotate in three dimensions along the orbit, the same results (high gain main lobe, suppressed sidelobes) can be achieved. It is important to work with orbital mechanics, not fight nature and physics.
Imagine an attempt to permanently "hover" on the "north" side of a circular equatorial orbit. All Kepler earth orbits are mapped onto planes which intersect the center of the earth, and our hovering object is actually on a different, slightly inclined orbit. If the object is free to follow the orbital mechanics without an external force, it will follow a slightly different inclination circular orbit that intersects the original orbital plane.
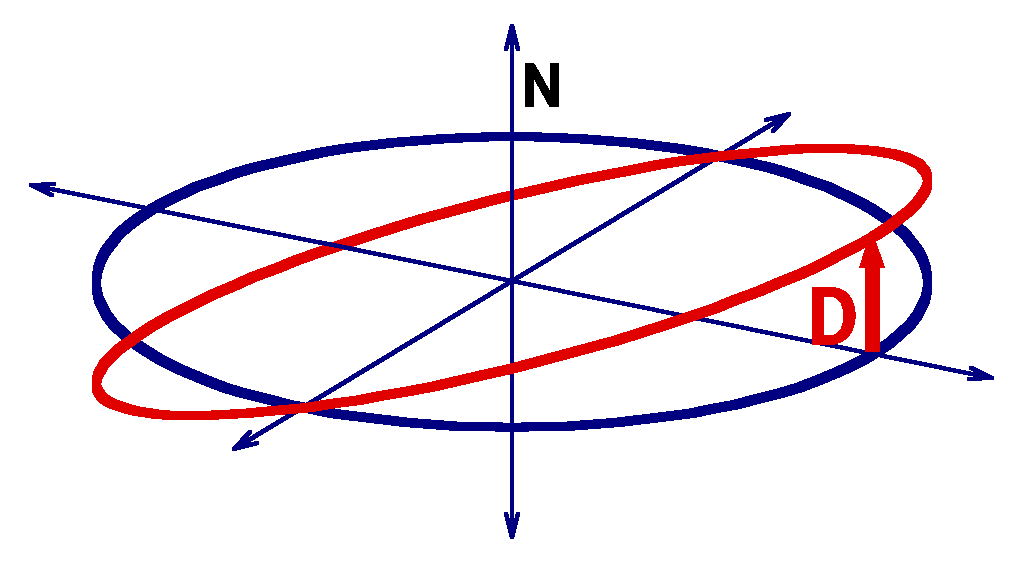
If the displacement of the unconstrained orbit differs from the equatorial orbit by d = D \sin{ \omega t } , then the acceleration is a = - \omega^2 D \sin{ \omega t } . Since \omega^2 = \mu / R^3 for a circular orbit without the J_2 perturbation, the peak acceleration is \mu D / R^3 . For μ = 398600.44 km3/s2, the acceleration at maximum displacement is given for various altitudes in the table below, as well as the accumulated \Delta V over a 10 year mission:
|
per meter of displacement D |
|||
Altitude |
Radius |
Acceleration |
10 year \Delta V |
|
km |
km |
μm/s2 |
m/s |
|
200 |
6578 |
1.400 |
441.9 |
|
600 |
6978 |
1.173 |
370.2 |
|
1000 |
7378 |
0.992 |
313.2 |
|
2000 |
8378 |
0.678 |
213.9 |
|
6411 |
12789 |
0.191 |
60.1 |
m288 |
35786 |
42164 |
0.0053 |
1.67 |
GEO |
These numbers are multiplied by the displacement; a 13 meter displacement results in 4812 m/s \Delta V over 10 years.
