Displacement and Acceleration
Arrays of satellites cannot maintain a constant displacement above or below the orbital plane without a constant (and significant) acceleration keeping them there. The ΔV needed over the lifetime of a satellite is beyond the range of high Isp engines. Further, it is unnecessary; by using constellations that evolve and rotate in three dimensions along the orbit, the same results (high gain main lobe, suppressed sidelobes) can be achieved. It is important to work with orbital mechanics, not fight nature and physics.
Imagine an attempt to permanently "hover" on the "north" side of a circular equatorial orbit. All Kepler earth orbits are mapped onto planes which intersect the center of the earth, and our hovering object is actually on a different, slightly inclined orbit. If the object is free to follow the orbital mechanics without an external force, it will follow a slightly different inclination circular orbit that intersects the original orbital plane.
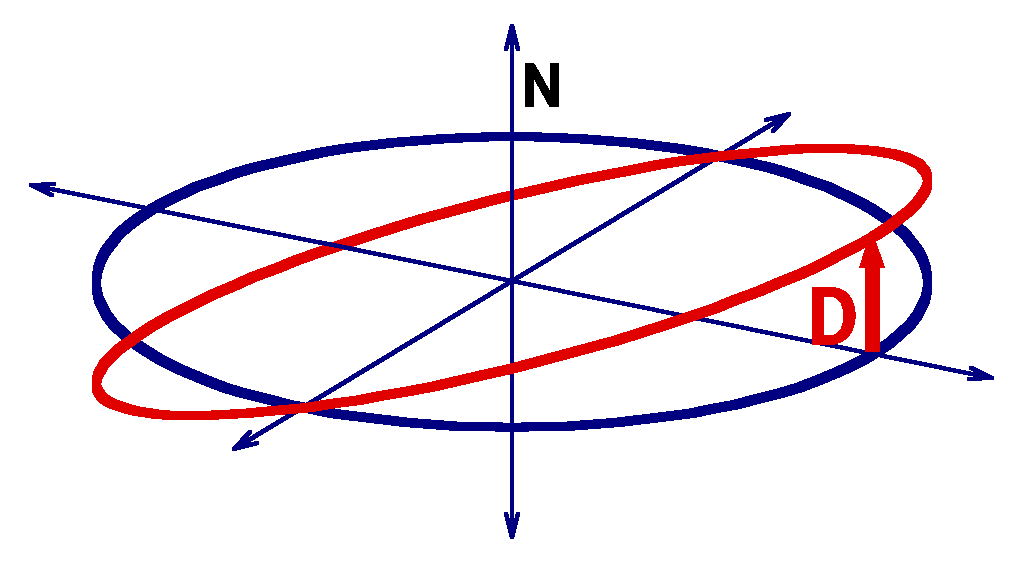
If the displacement of the unconstrained orbit differs from the equatorial orbit by d = D \sin{ \omega t } , then the acceleration is a = - \omega^2 D \sin{ \omega t } . Since \omega^2 = \mu / R^3 for a circular orbit without the J_2 perturbation, the peak acceleration is \mu D / R^3 . For μ = 398600.44 km3/s2, the acceleration at maximum displacement is given for various altitudes in the table below, as well as the accumulated \Delta V over a 10 year mission:
|
per meter of displacement D |
|||
Altitude |
Radius |
Acceleration |
10 year \Delta V |
|
km |
km |
μm/s2 |
m/s |
|
200 |
6578 |
1.400 |
441.9 |
|
600 |
6978 |
1.173 |
370.2 |
|
1000 |
7378 |
0.992 |
313.2 |
|
2000 |
8378 |
0.678 |
213.9 |
|
6411 |
12789 |
0.191 |
60.1 |
m288 |
35786 |
42164 |
0.0053 |
1.67 |
GEO |
These numbers are multiplied by the displacement; a 13 meter displacement at 600km altitude requires 4812 m/s \Delta V over 10 years. Even with a high efficiency VASIMR engine, the vehicle could be entirely fuel tanks, solar cells, and radiators, and have a hard time making that much \Delta V over a decade.
Alternatives to Continuous Displacements
Though it is more complicated to think about, it is a lot easier to deploy three dimensional arrays that naturally rotate and evolve as they orbit. 90° right angles do not stay right angles in these arrays, but relative positions can be very precise and predictable, with only infinitesimal corrections for J_2 effects and somewhat larger corrections for light pressure. Indeed, by modulating the light pressure with electrochomic panels, you can keep an array predictably positioned within fractions of a micron. The array evolutions will complicate the analysis, but an orbiting array turns at about a picoradian per microsecond, so the array has plenty of time to retarget communication beams and perform position tweaks. The main principle: Work with nature, and exploit its behavior, do not attempt to fight nature.
