|
Size: 4804
Comment:
|
Size: 4818
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 60: | Line 60: |
| Here's a plot versus time. Remember, the abscissa is degrees of the year, one degree=1.015 days . 30 degrees equals a month. The plot starts on the spring equinox, around March 23. | Here's a plot versus time. The x axis is degrees of the year, one degree=1.015 days, 30 degrees equals a month, 360 degrees equals a year. The plot starts on the spring equinox, around March 23. |
Earth Eclipse of Server Sky Arrays
If the Earth was perfectly round, and the poles were not inclined, arrays in the 12789km, 17280 second radius equatorial orbit would spend 2868 seconds per orbit shaded by the 6371km radius Earth ( = 17280 \times asin( 6371 / 12789 ) / 180^\circ ~ ).
In fact, the Earth has an equatorial radius of 6378.1 km, a polar radius of 6356.8 km, and an axial tilt of \phi = 23.439281° . The sun has an angular size of 0.53 degrees, and the Earth's atmosphere refracts light, meaning that the light dims gradually over approximately 30 seconds entering eclipse. For the rest of this analysis, we will ignore these gradual effects, pretend the sun is a point source at infinity, and calculate the hard cutoff time as a function of time of year.
The variable \beta represents the time of year in the northern hemisphere, from 0° in spring, 90° in summer, 180° in the fall, and 270° in winter.
Oblate Earth
The equatorial plane is tilted towards the sun by angle \theta_{eq} defined by:
\sin( \theta_{eq} ) = \sin( \beta ) \sin( \phi ) ~ ~ ~ see [Precession]
The earth can be approximated as an elliptical disk, a projection of a ellipsoidal spheroid with an equatorial radius R_E = 6,378,137 meters and a polar radius R_P = 6,356,752 meters. The edge of this elliptical disk follows the equation:
y = \sqrt{ ( R_E^2 - x^2 ) ( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 } ~ ~ ~ see [TiltingOblate]
The m288 orbit is a circle in the equatorial plane with a radius of R_{m288} . This circle projects into the X,Z plane as
y = \sin( \theta_{eq} ) \sqrt{ R_{m288}^2 - x^2 }
Two of the four points where these y values are equal are the points were the orbit enters or leaves the eclipse, so:
y_e = \sin( \theta_{eq} ) \sqrt{ R_{m288}^2 - x_e^2 } = \sqrt{ ( R_E^2 - x_e^2 ) ( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 }
Let's solve for x_e :
\sin( \theta_{eq} )^2 ( R_{m288}^2 - x_e^2 ) = ( R_E^2 - x_e^2 ) \left( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 \right)
x_e^2 \left( \left( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 \right) - \sin( \theta_{eq} )^2 \right) ~ = ~ R_E^2 \left( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 \right) - \sin( \theta_{eq} )^2 R_{m288}^2
x_e^2 \left( ( R_P / R_E )^2 ( 1 -\sin( \theta_{eq} )^2 ) \right) ~ = ~ R_P^2 - ( R_{m288}^2 + R_P^2 - R_E^2 ) \sin( \theta_{eq} )^2
\large x_e ~ = ~ \sqrt{ { R_P^2 - ( R_{m288}^2 + R_P^2 - R_E^2 ) \sin( \theta_{eq} )^2 } \over { ( R_P / R_E )^2 ( 1 -\sin( \theta_{eq} )^2 ) } }
Which simplifies to the following:
6,378,137 m |
R_E |
Equatorial Radius |
6,356,752 m |
R_P |
Polar Radius |
12,788,866 m |
R_{m288} |
m288 Orbit radius |
14,400.0 sec |
T_{orbit} |
sun-relative period |
23.439281° |
\phi |
axial tilt |
0° to 360° |
\beta |
time of year from spring equinox |
\Large x_e ~ = ~ R_E \sqrt{ { 1 - ( ( R_{m288}^2 + R_P^2 )/ R_E^2 ) - 1 ) \sin( \theta_{eq} )^2 } \over { 1 -\sin( \theta_{eq} )^2 } } ~ \approx 6,378,137 m \sqrt{ { 1 - 0.635085 \sin( \beta )^2 } \over { 1 - 0.158227 \sin( \beta )^2 } } ~ ~ ~ \sin( \theta_{eq} ) = \sin( \beta ) \sin( \phi )
The eclipse fraction F_E (fraction of the total orbit) is:
\large F_E = \arcsin( x_e / R_{m288} ) / \pi ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ assumes arcsin() in radians, if in degrees divide by 180°
The eclipse time T_E is
\large T_E = T_{orbit} \arcsin( x_e / R_{m288} ) / \pi ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
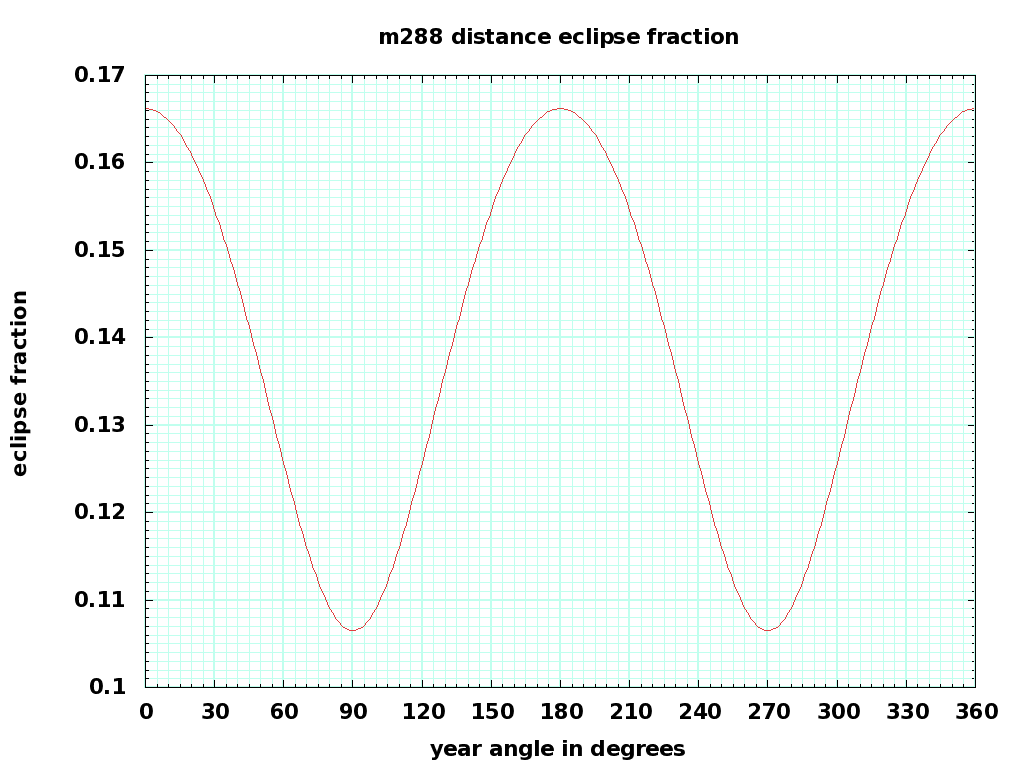
x_e varies from 4,199,446 to 6,378,137 meters, so the fraction-of-orbit F_E varies from 0.1065 to 0.1662, with an average of 0.1388, and eclipse time varies from 1534 to 2393 seconds with an average of 1999 seconds. The eclipse will be longest in spring and fall, shortest in summer and winter. The shortest eclipse periods correspond to surface peak power demands (heating and cooling), which is fortuitous. The cost of computing will be highest during summer in the temperate regions.
Here's a plot versus time. The x axis is degrees of the year, one degree=1.015 days, 30 degrees equals a month, 360 degrees equals a year. The plot starts on the spring equinox, around March 23.
source . . . output data . . . gnuplot control file
