Earth Eclipse of Server Sky Arrays

If the Earth was perfectly round, and the poles were not inclined, arrays in the 12789 km, 17280 second radius equatorial orbit would spend 2868 seconds per orbit shaded by the 6371km radius Earth ( = 17280 \times asin( 6371 / 12789 ) / 180^\circ ~ ).

In fact, the Earth has an equatorial radius of 6378.1 km, a polar radius of 6356.8 km, and an axial tilt of \phi = 23.439281° . The sun has an angular size of 0.53 degrees, and the Earth's atmosphere refracts light, meaning that the light dims gradually over approximately 30 seconds entering eclipse. For the rest of this analysis, we will ignore these gradual effects, pretend the sun is a point source at infinity, and calculate the hard cutoff time as a function of time of year.

The variable \beta represents the time of year in the northern hemisphere, from 0° in spring, 90° in summer, 180° in the fall, and 270° in winter.

Oblate Earth

The equatorial plane is tilted towards the sun by angle \theta_{eq} defined by:

\sin( \theta_{eq} ) = \sin( \beta ) \sin( \phi ) ~ ~ ~ see Precession

The earth can be approximated as an elliptical disk, a projection of a ellipsoidal spheroid with an equatorial radius R_E = 6,378,137 meters and a polar radius R_P = 6,356,752 meters. The edge of this elliptical disk follows the equation:

y = \sqrt{ ( R_E^2 - x^2 ) ( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 } ~ ~ ~ see TiltingOblate

The m288 orbit is a circle in the equatorial plane with a radius of R_{m288} . This circle projects into the X,Z plane as

y = \sin( \theta_{eq} ) \sqrt{ R_{m288}^2 - x^2 }

Two of the four points where these y values are equal are the points were the orbit enters or leaves the eclipse, so:

y_e = \sin( \theta_{eq} ) \sqrt{ R_{m288}^2 - x_e^2 } = \sqrt{ ( R_E^2 - x_e^2 ) ( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 }

Let's solve for x_e :

\sin( \theta_{eq} )^2 ( R_{m288}^2 - x_e^2 ) = ( R_E^2 - x_e^2 ) \left( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 \right)

x_e^2 \left( \left( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 \right) - \sin( \theta_{eq} )^2 \right) ~ = ~ R_E^2 \left( ( 1 - ( R_P / R_E )^2 ) \sin( \theta_{eq} )^2 + ( R_P / R_E )^2 \right) - \sin( \theta_{eq} )^2 R_{m288}^2

x_e^2 \left( ( R_P / R_E )^2 ( 1 -\sin( \theta_{eq} )^2 ) \right) ~ = ~ R_P^2 - ( R_{m288}^2 + R_P^2 - R_E^2 ) \sin( \theta_{eq} )^2

\large x_e ~ = ~ \sqrt{ { R_P^2 - ( R_{m288}^2 + R_P^2 - R_E^2 ) \sin( \theta_{eq} )^2 } \over { ( R_P / R_E )^2 ( 1 -\sin( \theta_{eq} )^2 ) } }

Which simplifies to the following:

\Large x_e ~ = ~ R_E \sqrt{ { 1 - ( ( R_{m288}^2 + R_P^2 )/ R_E^2 ) - 1 ) \sin( \theta_{eq} )^2 } \over { 1 -\sin( \theta_{eq} )^2 } } ~ \approx 6,378,137 m \sqrt{ { 1 - 0.635085 \sin( \beta )^2 } \over { 1 - 0.158227 \sin( \beta )^2 } } ~ ~ ~ \sin( \theta_{eq} ) = \sin( \beta ) \sin( \phi )

The eclipse fraction F_E (fraction of the total orbit) is:

\large F_E = \arcsin( x_e / R_{m288} ) / \pi ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ assumes arcsin() in radians, if in degrees divide by 180°

While this is going on, the earth is going around the sun, and the sun is making an apparent motion in the earth sky. This stretches the time in eclipse by this small factor:

\large stretch = 1.0 / ( 1.0 - ( T_{orbit}/Year ) )

That is also the correction factor from the sidereal to the synodic orbit. The eclipse time T_E is thus:

\large T_E = T_{synodic} \arcsin( x_e / R_{m288} ) / \pi

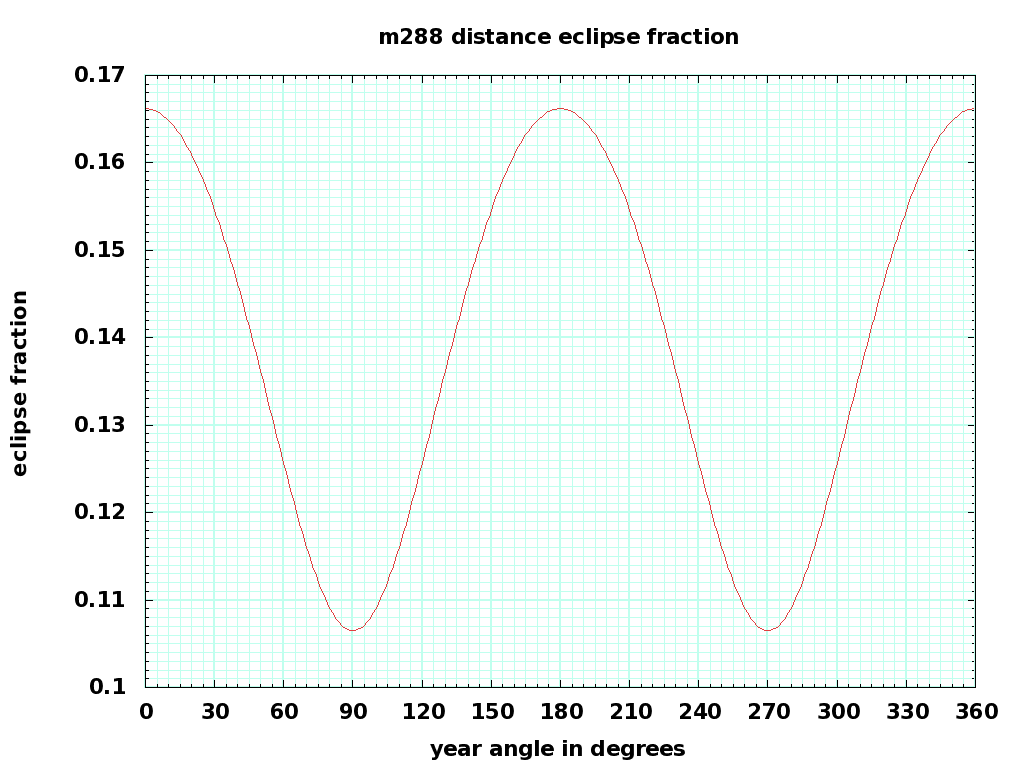
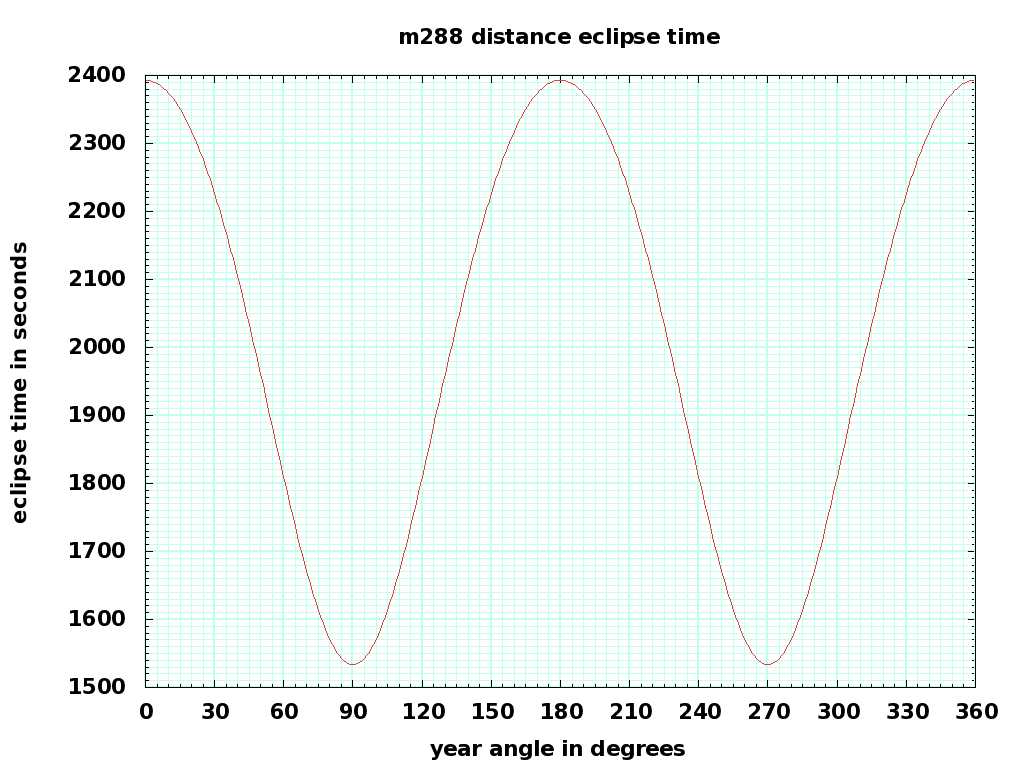
For m288, T_{synodic} = 14400 sec. This is noon to noon time, not the repeat time for a particular spot on the earth. x_e varies from 4,199,446 to 6,378,137 meters, so the fraction-of-orbit F_E varies from 0.1065 to 0.1662, with an average of 0.1388, and eclipse time varies from 1534 to 2393 seconds with an average of 1999 seconds. The eclipse will be longest in spring and fall, shortest in summer and winter. The shortest eclipse periods correspond to surface peak power demands (heating and cooling), which is fortuitous. The cost of terrestrial computing will be highest during summer in the temperate regions, when extra air conditioning is needed in data centers.

---

Here's plot of eclipse fraction and eclipse time versus the time in the year. The x axis is degrees of the year, one degree=1.015 days, 30 degrees equals a month, 360 degrees equals a year. The plot starts on the spring equinox, around March 23.

---

The eclipse fraction drops significantly near the summer and winter solstices. At a radius of 16043 km, the eclipse fraction drops to zero at the solstices. Above that altitude, the equation for x_e becomes imaginary around the solstices, andhe numerator of the square root drops below zero. That means that the orbit passes above or below the top of the earth ellipse, and the satellites are always in sunlight around the solstices.

---

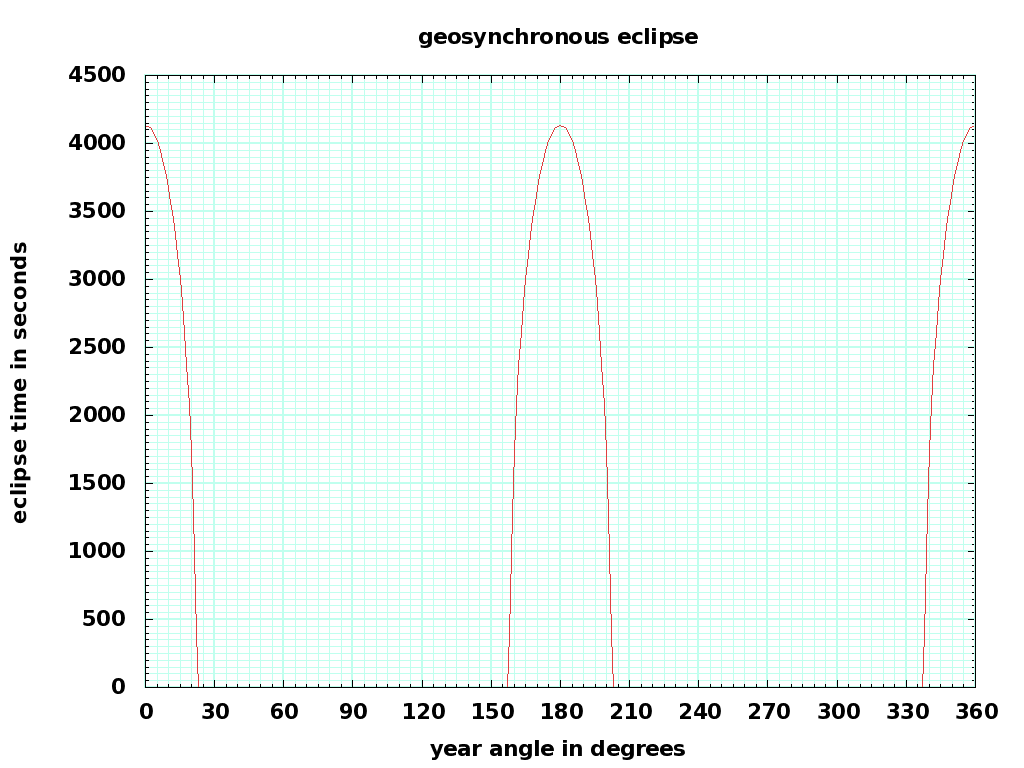
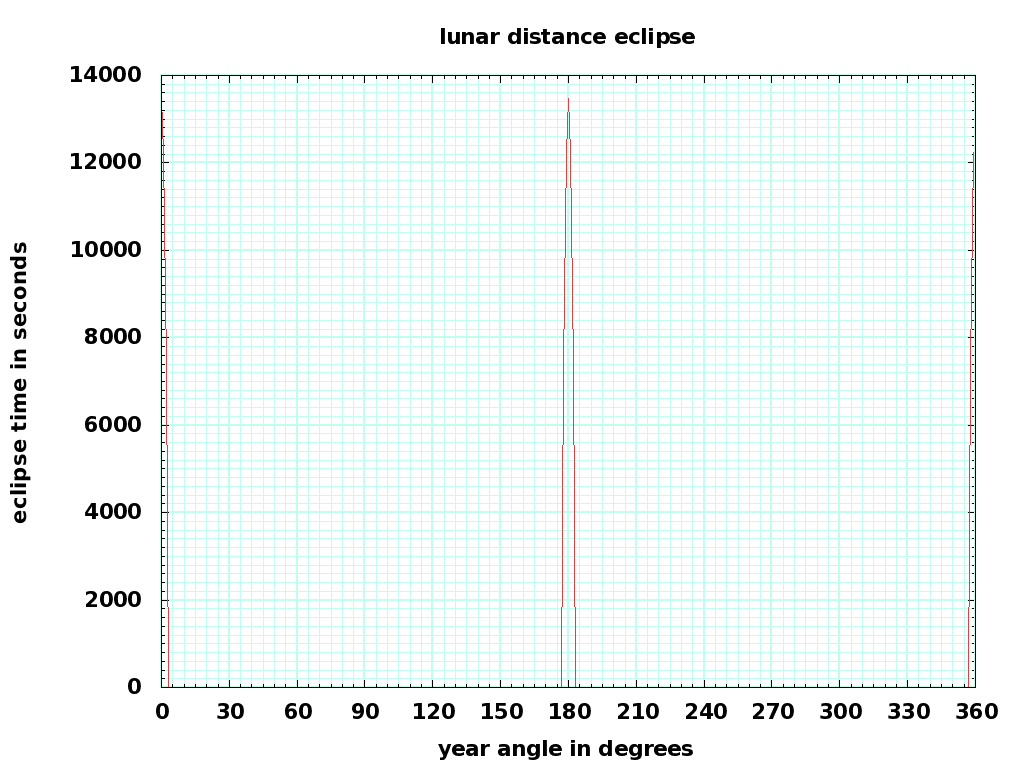
Here are the eclipse times for GEO and for the Moon. Note that a lunar-distance eclipse happens only when the mean anomaly (position around the orbit) is right; most times, this occurs at the wrong time of year. It is possible to tune the period and inclination of an orbit beyond the moon ( to an integer divisor of a year) so eclipses never happen.