|
Size: 4220
Comment:
|
Size: 5587
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
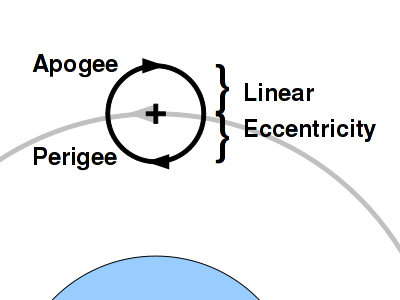
Note - this information must be heavily modified to account for the 3.7 degree daily precession of the m288 equatorial orbit because of the J2 spherical harmonic of the Earth's oblateness. This will probably require an apogee towards the sun, about 50 km linear eccentricity. MORE LATER |
|
| Line 22: | Line 24: |
| For $ a_L = 17 \mu m / s ^ 2 $ and the m288 orbit ( P = 4*3600 = 14400 seconds ), this is around '''200 km'''. | For $ a_L = 17 \mu m / s ^ 2 $ and the m288 orbit ( P = 4*3600 = 14400 seconds ) and a year of 31556926 seconds, this is around '''200 km'''. |
| Line 27: | Line 29: |
== Orbital Decay or Expansion == The above discussion assumes that the server-sat is under control, and face-forwards towards the sun for maximum power. This is best for computation productivity. However, it is also possible to raise or lower the orbit somewhat by tilting the server-sat at various parts of the orbit. For example, if the server-sat is tilted 60 degrees away from the sun while orbiting towards it (cutting light power and light pressure in half) and face-on towards the sun while orbiting away from it, it will slowly gain orbital speed, about 2cm/sec per orbit, or 42 meters per second per year, raising the orbit. After a few decades, it might be close enough to the moon to either be slingshotted into solar orbit, or sent plunging back to reenter. Over a very long time, tumbling and completely out of control, random variations in up and down orbit acceleration would eventually drive it up and down, probably in something resembling a random walk. This process is likely to be very slow. MORE LATER |
Light Pressure Modified Orbits
Note - this information must be heavily modified to account for the 3.7 degree daily precession of the m288 equatorial orbit because of the J2 spherical harmonic of the Earth's oblateness. This will probably require an apogee towards the sun, about 50 km linear eccentricity. MORE LATER
|
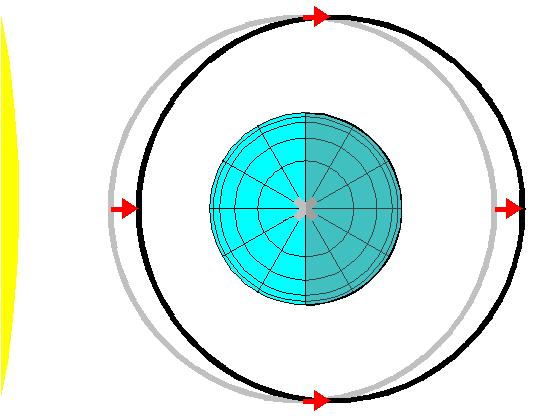
Solar light pressure is useful for maneuvering, but it distorts orbits. Light pressure slows objects orbiting towards the sun, and speeds up objects orbiting away from it. This raises and lowers portions of the orbit. A slightly elliptical orbit with perigee towards the sun will rotate. With proper matching of eccentricity, the apogee and perigee will complete one rotation per year. |
|
An orbit can be viewed in a rotating frame of reference centered on a point in circular orbit. For small eccentricities, an elliptical orbit traces a circle in this frame, rotating in the opposite direction from the orbit itself. That is, if the orbit is eastwards, rotating counterclockwise when viewed from the north, the orbit rotates clockwise in the rotating frame. If the frame is positioned with the earth below, the top of the circle is the apogee and the bottom of the circle is the perigee, so the orbit moves backwards (to the right) compared to the "circular center" at apogee (more slowly), and forwards (to the left) at perigee (more rapidly). |
If the orbit precesses once per year, then the vector of the linear eccentricity makes one complete rotation per year. Each orbit adds a little bit of rotation to that vector.
Viewed closely, the displacement caused by light pressure looks like a cycloid ruffle on the orbit circle. In the rotating frame of reference, the sun appears to rotate around the orbit circle once per orbit period, with the light pressure acceleration pointing away from the sun. The sun "disappears" during the eclipsed part of the orbit, and this changes the math somewhat, but the major effects are caused when the object is moving towards or away from the sun, on the sides of the ellipse. This rough estimate ignores eclipses.
Referenced to a zero angle at apogee, the light pressure acceleration in the x direction is a_x = a_L sin( \omega t ) and a_y = a_L cos( \omega t ) . a_L is approximately 17 \mu m / s ^ 2 for a 100 micron thick server-sat. Assuming we start at zero position and velocity, then doubly integrating each of these equations results in x = ( a_L / \omega^2 ) ( \omega t - sin ( \omega t ) ) and y = ( a_L / \omega^2 ) ( 1 - cos ( \omega t ) ) . This is the formula for a cycloid. After one orbit period P ( \omega = 2 \pi / P ) x has shifted by a_0 P^2 / 2 \pi . The sum of these increments add up to the orbit circle over one year Y, so x Y / P = 2 \pi \epsilon r_0 . Solving for the linear eccentricity, \epsilon r_0 = ( a_L P Y )/( (2 \pi)^2 . For a_L = 17 \mu m / s ^ 2 and the m288 orbit ( P = 4*3600 = 14400 seconds ) and a year of 31556926 seconds, this is around 200 km.
Lighter server-sats will have higher light pressure acceleration, and orbit with larger linear eccentricities. This will result in larger relative displacements. Regions of m288 with higher and lower server-sat area-to-mass ratios should be separated by hundreds or thousands of kilometers.
Perhaps the m360 and m480 orbits should be reserved for lighter and lighter server-sats, assuming that the trend over time will be towards lighter server-sats, better boosters, and more sophisticated latency management. Solar power arrays at lunar distances will be very light, but will have a lot more room for linear eccentricity displacements.
Orbital Decay or Expansion
The above discussion assumes that the server-sat is under control, and face-forwards towards the sun for maximum power. This is best for computation productivity. However, it is also possible to raise or lower the orbit somewhat by tilting the server-sat at various parts of the orbit. For example, if the server-sat is tilted 60 degrees away from the sun while orbiting towards it (cutting light power and light pressure in half) and face-on towards the sun while orbiting away from it, it will slowly gain orbital speed, about 2cm/sec per orbit, or 42 meters per second per year, raising the orbit. After a few decades, it might be close enough to the moon to either be slingshotted into solar orbit, or sent plunging back to reenter.
Over a very long time, tumbling and completely out of control, random variations in up and down orbit acceleration would eventually drive it up and down, probably in something resembling a random walk. This process is likely to be very slow.
MORE LATER