|
Size: 14544
Comment:
|
Size: 14719
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 4: | Line 4: |
| Summary: while 50 micron thinsats are probably manufacturable, they may be a bit too thin, perhaps by a factor of 2. Light-pressure-related eccentricity gets very large if the thinsats are too light. THIS NEEDS FURTHER STUDY. | Summary: while 50 micron thinsats are probably manufacturable, they may be a bit too thin, perhaps by a factor of 2. Light-pressure-related eccentricity gets larger as the thinsats grow thinner. THIS NEEDS FURTHER STUDY. |
| Line 177: | Line 177: |
| The locus of all these orbits will be a "double Möbius" strip (one full turn), with one edge along the circular central orbit and the other edge wrapping around it toroidally. |
Light Pressure Modified Orbits
Summary: while 50 micron thinsats are probably manufacturable, they may be a bit too thin, perhaps by a factor of 2. Light-pressure-related eccentricity gets larger as the thinsats grow thinner. THIS NEEDS FURTHER STUDY.
Light pressure effects modify thinsat array orbits. In the nominal orbit, thinsats are at "half thrust", with each thruster half mirror and half transparent. Variations to full or zero reflectivity, and full or zero thrust, allow each thinsat to maneuver in relation to the array, or for the array as a whole to maneuver around its assigned centerpoint. The following is an analysis of two effects, earth oblateness and nominal half-thrust light pressure, on the orbit. We will assume that the arrays maintain a constant, slightly elliptical orbit that precesses once per year in the equatorial plane. We will assume continuous illumination tangential to the equatorial plane, and zero light pressure effects from Earth albedo or black-body radiation, and no solar or lunar tides. These assumptions are somewhat crude approximations to get us into the ballpark of a solution. Precise solutions will probably demand accurate numerical solutions simulating many years of orbital evolution.
Earth Oblateness
For "heavy" thinsats relatively close to the earth, such as 3 gram satellites at m288, the dominant deviation from a perfect Kepler orbit is caused by the J_2 spherical harmonic of the gravity field, in turn caused by the oblateness of the spinning Earth. For small eccentricities, the eastward precession of the perigee of one elliptical equatorial orbit is proportional to the J_2 term of the WGS84 model ( -1.082626683E-03 , see Pisacane 2008 ) and the inverse of the orbit radius squared. For small eccentricity and inclination, the precession, expressed as the number complete precessions per year, is N_{pr} \approx -3 J_2 ( Y / T ) ( R_e / A ) ^ 2 ~ ~ where
N_{pr} |
precessions per year caused by oblateness |
J_2 |
spherical harmonic of gravity causing oblateness |
Y |
year period in seconds, |
T |
orbit period in seconds |
Y/T |
number of orbits per year |
R_e |
earth equatorial radius = 6378 km |
A |
orbit semimajor axis (radius if circular) |
Note: Pisacane's formula (5.47b) is for d \omega / dt in radians per second, and is in terms of n = 2 \pi / T . Dividing both sides by 2 \pi and multiplying by Y seconds per year gives the number of complete 360° (=2π radian) precessions per year. His more accurate formula uses a ( 1 - e^2 ) instead of A and has a correction for inclination, but both inclination and ellipsicity are small for these near-equatorial near-circular orbits, so we can use the above approximation to a few percent accuracy.
orbit |
radius (RE) |
orbits/year |
N_{pr} |
LEO |
1.047 |
5758.5 |
17.061 |
m288 |
2.005 |
2191.5 |
1.771 |
m360 |
2.264 |
1826.2 |
1.157 |
m480 |
2.627 |
1461.0 |
0.688 |
m720 |
3.182 |
1095.7 |
0.351 |
m1440 |
4.168 |
730.5 |
0.137 |
GEO |
6.611 |
365.2 |
0.027 |
To keep a thinsat orbit in the same orbit and orientation to the sun, the light pressure must retard the precession at m288 and m360, and advance it at m480 and m720, so that the total precessions per year is one. More complicated orbit evolution may allow different ratios, however, eccentricity should not accumulate over many years or the apogee and perigee will eventually intersect other orbital bands, causing collisions.
Thinsat characteristics
Light pressure parameters |
|||
Light Power |
1367 |
W/m2 |
|
Speed of Light |
2.998e+8 |
m/s |
|
Light pressure |
4.56e-6 |
kg/m-s2 |
|
Thinsat parameters |
|||
mass |
3e-3 |
kg |
|
thickness |
5e-5 |
m |
|
density |
2.5e+3 |
kg/m3 |
|
volume |
1.2e-6 |
m3 |
|
area |
2.4e-2 |
m2 |
|
length |
18.5e-2 |
m |
rounded thruster top |
force |
1.0944e-7 |
kg-m/s2 |
|
acceleration |
3.648e-5 |
m/s2 |
|
Light Pressure
A useful starting analysis is in E. M. Soop, "Handbook of Geostationary Orbits". Soop's analysis is for geostationary orbits, which are rarely in eclipse and much less subject to J2. perturbations. However, Soop's analysis is a good starting point. The book is practical, focused on satellite operation, the math is moderate, and the references are rather skimpy.
Soop analyzes the geostationary orbit in the cartesian MEGSD (Mean Equatorial Geocentric System of Date) coordinate system (pg. 15). This system is approximate and quasi-inertial; very accurate analyses will require full numerical solutions. The X-Y plane of MEGSD is the Earth's equatorial plane (which slowly precesses 0.014° per year), with the x direction oriented sidereally, towards the Vernal Equinox or First Point of Aries, where the equatorial plane and the ecliptic plane intersect. The Z direction is north.
Soop describes the various orbital parameters as both scalars (pg 21) and vectors. Unlike Soop, I will use \vec{ x } instead of \overline{ x } .
|
scalar |
vector |
|
semimajor axis |
a |
||
eccentricity |
e |
\vec{ e } |
|
inclination |
i |
\vec{ I } |
|
right ascension of the ascending node |
\Omega |
||
argument of perigee |
\omega |
||
true anomaly |
\nu |
||
unperturbed orbit angle |
s |
||
radius |
r |
\vec{ r } |
|
velocity |
dr / dt |
d\vec{ r }/dt |
|
unperturbed orbit velocity |
V = \sqrt{ \mu / A } |
|
similar to Soop page 39 |
apogee |
r_a |
||
perigee |
r_p |
||
period |
T = 2 \pi \sqrt{ a^3/\mu } |
||
radial velocity |
V_r = V (e_x~sin~s~-~e_y~cos~s) |
|
similar to Soop page 39 |
tangential velocity |
V_t = 2 V (e_x~cos~s~+~e_y~sin~s) |
|
similar to Soop page 39 |
orthogonal (North) velocity |
V_o = V (i_x~sin~s~-~i_y~cos~s) |
|
similar to Soop page 39 |
\vec{ I } = \left( \matrix{ sin~i~sin~\Omega \\ -sin~i~cos~\Omega \\ cos~i } \right)
\vec{ r } = \left( \matrix{ x \\ y \\ z } \right) = { { a( 1 - e^2 ) } \over { 1 + 3 cos~\nu } } \left( \matrix { cos~\Omega~cos( \omega+\nu ) - sin~\Omega~sin( \omega+\nu )~cos~i \\ sin~\Omega~cos( \omega+\nu ) - cos~\Omega~sin( \omega+\nu )~cos~i \\ sin( \omega+\nu )~sin~i } \right) . . . Soop pg 25
A \equiv MXXX unperturbed orbit radius . . . similar to Soop page 26
\vec{ i } = ( i~sin( \Omega ), i~cos( \Omega ) ) . . . Soop pg 27
\vec{ e } = ( e~cos( \Omega + \omega ), e~sin( \Omega +\omega ) ) . . . Soop pg 27
r \approx A + \delta a~-~A e~cos~\nu . . . Soop pg 29
s_b is angle at thrust . . . Soop pg 53
\Delta \vec{ e } = { { 2 \Delta V } \over V } \left( \matrix{ cos~s_b \\ sin~s_b } \right) . . . Soup pg 54
\lambda = 3.65e-5 s-2 is the light pressure acceleration, which is the solar pressure ( 4.56e-6 N/m2 ) times the area to mass ratio, 8 m2 = ( 0.024 m2 / 0.003 kg ) for a 50 μ m thinsat. . . similar to Soop pg 93
s is sidereal angle of orbit . . . Soop pg 93 text
s_s is sidereal angle of Sun . . . Soop pg 93 text
{ { d\vec{ e } } \over dt } = { 2 \over V } \left( \matrix{ cos~s \\ sin~s } \right) { { d V_t } \over dt } + { 1 \over V } \left( \matrix{ sin~s \\ -cos~s } \right) { { d V_r } \over dt } . . . Soop pg 93
{ { \partial \vec{ e } } \over { \partial t } } = { \lambda \over { 2 \pi V } } \int_0^{2\pi} \left[ 2 \left( \matrix{ cos~s \\ sin~s } \right) sin( s-s_s ) - \left( \matrix{ sin~s \\ -cos~s } \right) cos(s-s_s) \right] ds . . . Soop pg 93
{ { \partial \vec{ e_{lambda} } } \over { \partial t } } = { { 3 \lambda } \over { 2 V } } \left( \matrix{ - sin~s_s\\cos~s_s } \right) perpendicular to the Sun, perturbing the eccentricity vector eastward . . . Soop page 95
Y = one year . . . Soop page 95
\vec{ e_{\lambda} } ( t ) = { { 3 P \sigma Y } \over { 4 \pi V } } \left( \matrix{ cos~s_s\\sin~s_s } \right) . . . Soop page 95
Without the J2 modifications, a light-pressure-modified orbit(with \vec e and perigee pointing towards the sun ) for a 3 gram, 240cm2 thinsat ( \sigma = 8 m-1s^-2> would have a light pressure eccentricity of:
e_{\lambda} = { { 3 \lambda Y } \over { 4 \pi V } } = { { 3\times3.65e-5\times3.156e7 } \over { 4\times\pi\times5582.74 } } = 0.049
The eccentricity of the light modified orbit is around 0.05 . If the thinsat is thinner, that gets larger. It also gets larger for more distant orbits ( M360, M480, etc.). Proportional to period T1/3
Inclination to the Ecliptic
Because of the inclination of the orbit relative to the ecliptic, some of the light pressure is towards the south during summer and the north during winter. The eccentricity-modifying light pressure is a function of the sun's declination \delta_\odot :
\lambda = \lambda_0 ~ cos ~ \delta_\odot
where:
\delta_\odot = \arcsin \left [ \sin \left ( -23.44^\circ \right ) \cdot \cos \left ({{360^{\circ}\times(day+10)}\over{365}} \right ) \right ] ~ ~ ~ where day is the day of the year starting with Jan 1 = 0
thus
\lambda = \lambda_0 \sqrt{ 1 - \left [ \sin \left ( -23.44^\circ \right ) \cdot \cos \left ({{360^{\circ}\times(day+10)}\over{365}} \right ) \right ]^2 }
\langle \lambda \rangle \approx 0.9592 ~ \lambda_0 so e_{\lambda} is reduced somewhat, to 0.047 .
Modifications for earth shadow eclipse time
The eclipse time has a small effect, because we are only subtracting an acceleration approximately equal to sin2 of the +/- 30° angle behind the earth. Integrating from -150° to 150° subtracts approximately 1/24 of the effect, so e_{\lambda} is reduced to about 0.045 .
Combining with the J2 Modification
The simplest case for M288 is an eccentricity vector diagram like so:
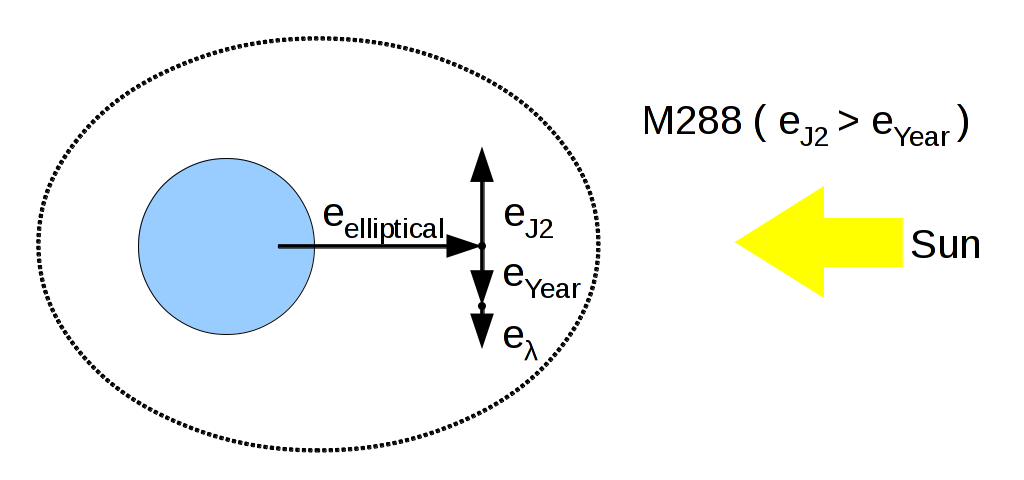
For a bounded elliptical M288 orbit, e_{J2} = 1.771 \times e and e_{ year } = e , so with apogee towards the sun, e_{ \lambda } = 0.771 \times e . That means that for a 50μm 8 m2/kg thinsat, e = 0.045 / 0.771 or 0.058, or perhaps a little larger because of the twice-annual variation in tangential light acceleration. Assume that the distance to orbits near M288 (for example, LAGEOS) should be at least 0.06*12789 km, so there should be no valuable equatorial crossers between 12000 and 13300 km .
FIXME ... the LAGEOS satellites cross the equator at around 12230km - WE MAY NEED TO MAKE THE 50μm THINSAT HEAVIER!!! Or maybe our rising and descending nodes can be made to match LAGEOS in some manner, so we always stay many kilometers away. Needs more analysis!!!
MORE LATER
M360 orbits have a J2 excess of 0.157 instead of 0.771, which means that the eccentricity to mass ratio will be almost 5 times larger than M288. M360 does not look like a practical orbit for low mass thinsats. Cheap launch and ballast will change this.
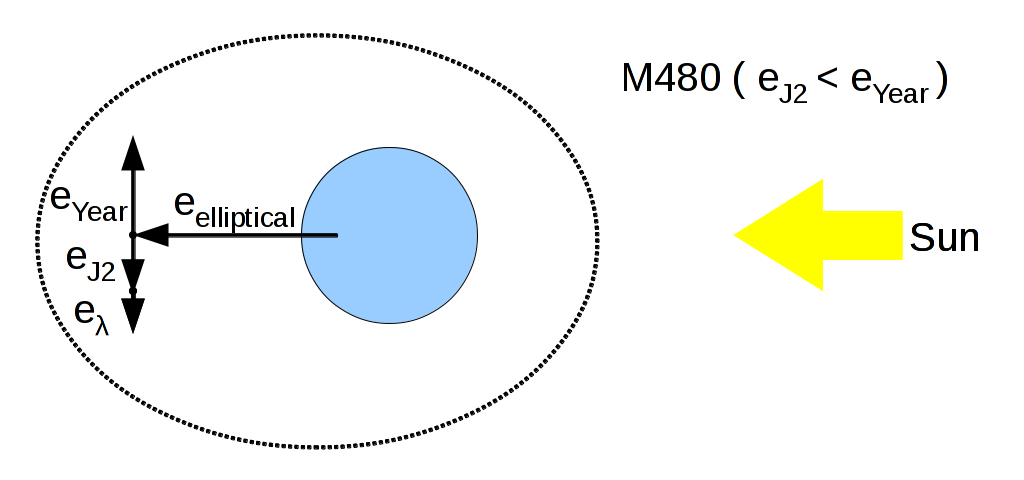
The M480 orbit ( 16756km ) is slower so $ e_{\lambda} is larger:
e_{\lambda488} = { { 3 \lambda Y } \over { 4 \pi V } } = { { 3\times3.65e-5\times3.156e7 } \over { 4\times\pi\times 4877.51 } } = 0.056, reduced to perhaps 0.55 with eclipse effects.
For a bounded elliptical M480 orbit, e_{J2} = 0.688 \times e and e_{ year } = e , so with perigee towards the sun, e_{ \lambda } = 0.312 \times e . That means that for a 50μm 8 m2/kg thinsat, e = 0.055 / 0.312 or 0.176 . Assume that the distance to orbits near M480 should be at least 0.18*16756 km, so there should be no valuable equatorial crossers between 13700 and 19800 km . This is a very wide band; we probably must make m480 thinsats heavier.
Inclination - Flattened Toroidal Orbit
Because of the eccentricity, we will incline the orbit, so that the central orbit can be set aside for heavier thinsats. We should consider a flattened torus so that this orbit does not go too far south or north. If we make the inclination for the M288 orbit ( e = 0.058 ) 1°, then the orbit passes above and below the 12789 km central orbit by 223 km, compared to the 740 km sideways distance. The circular orbital speed at M288 is 5583 m/s. The relative velocity of the two orbits at crossing ( r = A, cos( \theta ) = -e = 0.058, or \theta = 93.3° ) is:
tangential |
e V cos( \theta ) = e^2 V |
18.8 m/s |
radial |
e V sin( \theta ) |
323.3 m/s |
total |
e V |
323.8 m/s |
The "velocity shear" across the orbit is 1.45 m/s per km or 1.45e-3 / second. If we imagine a series of increasing-weight thinsats around the central orbit, lighter at the edges and denser near the central orbit, then M288 orbits that differ in velocity by 1.45 m/s will always more than 1 km apart.
The locus of all these orbits will be a "double Möbius" strip (one full turn), with one edge along the circular central orbit and the other edge wrapping around it toroidally.
MORE LATER
Old (incorrect) analysis removed.
