|
Size: 8396
Comment:
|
Size: 8557
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 8: | Line 8: |
| For "heavy" server-sats relatively close to the earth, such as 7 gram satellites at m288, the dominant deviation from a perfect Kepler orbit is caused by the "J2" spherical harmonic of the gravity field, in turn caused by the oblateness of the spinning Earth. For small eccentricities, the J2 term of the WGS84 model ( -1.082626683E-03 , see Pisacane 2008 ), times the inverse of the orbit radius squared, scales the eastward precession of the perigee of an elliptical equatorial orbit. This precession can be expressed as the number complete precessions per year as $ N \approx -3 J_2 ( Y / P ) ( R_e / R_s ) ^ 2 $ where | For "heavy" server-sats relatively close to the earth, such as 7 gram satellites at m288, the dominant deviation from a perfect Kepler orbit is caused by the "J2" spherical harmonic of the gravity field, in turn caused by the oblateness of the spinning Earth. For small eccentricities, the J2 term of the WGS84 model ( -1.082626683E-03 , see Pisacane 2008 ), times the inverse of the orbit radius squared, scales the eastward precession of the perigee of an elliptical equatorial orbit. The precession, expressed as the number complete precessions per year, is $ J \approx -3 J_2 ( Y / P ) ( R_e / R_s ) ^ 2 $ where $ J $ \equiv precessions per year caused by oblateness, $ J_2 $ \equiv spherical harmonic of gravity causing oblateness, $ Y $ \equiv year period in seconds, $ P $ \equiv orbit period in seconds, $ Y/P $ \equiv number of orbits per year, $ R_e $ \equiv earth equatorial radius = 6378km, $ R_s $ \equiv orbit equatorial radius. |
| Line 10: | Line 17: |
| $ Y $ = year period in seconds $ P $ = orbit period in seconds $ Y/P $ = number of orbits per year $ R_e $ = earth equatorial radius = 6378km $ R_s $ = orbit equatorial radius |
|| orbit || radius (RE) || orbits/year || J || || LEO || 1.047 || 5758.5 || 17.061 || || m288 || 2.005 || 2191.5 || 1.771 || || m360 || 2.264 || 1826.2 || 1.157 || || m480 || 2.627 || 1461.0 || 0.688 || || m720 || 3.182 || 1095.7 || 0.351 || || m1440 || 4.168 || 730.5 || 0.137 || || GEO || 6.611 || 365.2 || 0.027 || |
| Line 16: | Line 26: |
| || orbit || radius (RE) || orbits/year || precessions/year || || LEO || 1.047 || 5758.5 || 17.061 || || m288 || 2.005 || 2191.5 || 1.771 || || m360 || 2.264 || 1826.2 || 1.157 || || m480 || 2.627 || 1461.0 || 0.688 || || m720 || 3.182 || 1095.7 || 0.351 || || m1440 || 4.168 || 730.5 || 0.137 || || GEO || 6.611 || 365.2 || 0.027 || |
An orbit that always appears in the same spot in the sky at the same time every day is logistically simpler. It would precess once per year. As we will see, light pressure causes an eccentric orbit with apogee towards the sun to precess retrograde ( negative ) per year, while an orbit with perigee towards the sun precesses prograde (positive). We make up the differece, plus or minus, with light pressure. For orbits like m360, the light pressure effects on precession must be small to make up the small difference, requiring high-mass server-sats or large eccentricity orbits. Perhaps m360 should be reserved for high mass satellites like the O3B constellation. |
| Line 25: | Line 28: |
| It is convenient to design for an orbit that always appears in the same spot in the sky, every day. That would be an orbit that precesses once per year. As we will see, light pressure causes an eccentric orbit with apogee towards the sun to precess retrograde ( negative ) per year, while an orbit with perigee towards the sun precesses prograde (positive). We can use light pressure to make up the difference, plus or minus, if it is small. For orbits like m360, the light pressure effects must be small to make up the small difference, which will be difficult for low-mass server-sats with small eccentricity orbits. Perhaps this orbit should be reserved for high mass satellites like O3B. |
== Light Pressure == |
| Line 28: | Line 30: |
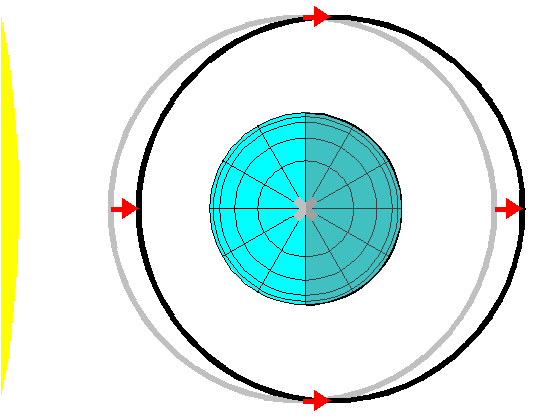
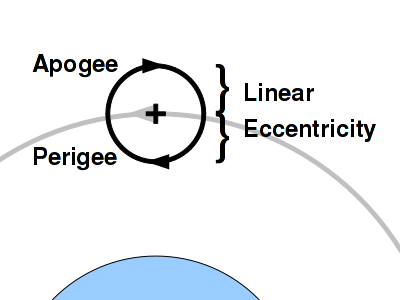
| The following needs to be modified - MORE LATER | ||{{attachment:NavigationV01/light-shift1.png|orbit from the north|width=300px}}|| Solar light pressure is useful for maneuvering, but it distorts orbits. Light pressure slows objects orbiting towards the sun, and speeds up objects orbiting away from it. This raises and lowers portions of the orbit. A slightly elliptical orbit with perigee towards the sun will precess prograde, while an orbit with apogee towards the sun will precess retrograde. With proper matching of eccentricity, and added to the J2 precession the apogee and perigee will complete one precession per year. || ||{{attachment:orbitcircle.png|orbit circle|width=300px}}|| An orbit can be viewed in a rotating frame of reference centered on a point in circular orbit. For small eccentricities, an elliptical orbit traces a circle in this frame, rotating in the opposite direction from the orbit itself. That is, if the orbit is eastwards, rotating counterclockwise when viewed from the north, the orbit rotates clockwise in the rotating frame. If the frame is positioned with the earth below, the top of the circle is the apogee and the bottom of the circle is the perigee, so the orbit moves backwards (to the right) compared to the "circular center" at apogee (more slowly), and forwards (to the left) at perigee (more rapidly).<<BR>><<BR>>An elliptical orbit is distorted from a circular one by the distance between the focii of the ellipse. The distance from the center to each focus, or the eccentricity times the semimajor axis, is called the ''linear eccentricity'' of the ellipse, or $ \epsilon r_0 $. The linear eccentricity is the radius of the orbit circle in the rotating frame. || |
| Line 30: | Line 33: |
| ||{{attachment:NavigationV01/light-shift1.png|orbit from the north|height=200px}}|| Solar light pressure is useful for maneuvering, but it distorts orbits. Light pressure slows objects orbiting towards the sun, and speeds up objects orbiting away from it. This raises and lowers portions of the orbit. A slightly elliptical orbit with perigee towards the sun will rotate. With proper matching of eccentricity, the apogee and perigee will complete one rotation per year.<<BR>><<BR>>'''This section does not include the effects of the Earth's oblateness, albedo, and black body radiation, nor the eclipse of the sun once per orbit, effects having similar magnitude to the solar light pressure. The final target orbit will be significantly different than the one discussed here.''' || ||{{attachment:orbitcircle.png|orbit circle|height=200px}}|| An orbit can be viewed in a rotating frame of reference centered on a point in circular orbit. For small eccentricities, an elliptical orbit traces a circle in this frame, rotating in the opposite direction from the orbit itself. That is, if the orbit is eastwards, rotating counterclockwise when viewed from the north, the orbit rotates clockwise in the rotating frame. If the frame is positioned with the earth below, the top of the circle is the apogee and the bottom of the circle is the perigee, so the orbit moves backwards (to the right) compared to the "circular center" at apogee (more slowly), and forwards (to the left) at perigee (more rapidly).<<BR>><<BR>>An elliptical orbit is distorted from a circular one by the distance between the focii of the ellipse. The distance from the center to each focus, or the eccentricity times the semimajor axis, is called the ''linear eccentricity'' of the ellipse, or $ \epsilon r_0 $. The linear eccentricity is the radius of the orbit circle in the rotating frame. || If the orbit precesses once per year, then the vector of the linear eccentricity makes one complete rotation per year. Each orbit adds a little bit of rotation to that vector. |
Ignoring the J_2 spherical harmonic, if the orbit precesses once per year, then the vector of the linear eccentricity makes one complete rotation per year. Each orbit adds a little bit of rotation to that vector, and that little bit of rotation is the sum of the light pressure and the J2 perturbations. |
| Line 42: | Line 40: |
| Assuming we start at zero position and velocity, then doubly integrating each of these equations results in $ x = ( a_L / \omega^2 ) ( \omega t - sin ( \omega t ) ) $ and $ y = ( a_L / \omega^2 ) ( 1 - cos ( \omega t ) ) $. This is the formula for a cycloid. After one orbit period $P$ ( $\omega = 2 \pi / P $ ) x has shifted by $ a_0 P^2 / 2 \pi $. The sum of these increments add up to the orbit circle over one year $Y$, so $ x Y / P = 2 \pi \epsilon r_0 $. Solving for the linear eccentricity, $ \epsilon r_0 = ( a_L P Y )/( (2 \pi)^2 $. For $ a_L = 17 \mu m / s ^ 2 $ and the m288 orbit ( P = 4*3600 = 14400 seconds ) and a year of 31556926 seconds, this is around '''200 km'''. |
Starting at zero position and velocity, then doubly integrating each of these equations results in $ \Delta x = ( a_L / \omega^2 ) ( \omega t - sin ( \omega t ) ) $ and $ \Delta y = ( a_L / \omega^2 ) ( 1 - cos ( \omega t ) ) $. This is the formula for a cycloid. After one orbit period $P$ ( $\omega = 2 \pi / P $ ) $ \Delta x $ has shifted by $ a_L P^2 / 2 \pi $. The sum of these increments, '''plus J''', add up to the orbit circle over one year $Y$, so $ \Delta x Y / P = 2 \pi ( 1 - J ) \epsilon r_0 $. Solving for the linear eccentricity, $ \epsilon r_0 = ( a_L P Y )/( 1 - J ) (2 \pi)^2 )$. For $ a_L = 17 \mu m / s ^ 2 $ and the m288 orbit ( P = 4*3600 = 14400 seconds, J = 1.771 ) and a year of 31556926 seconds, this is approximately '''-250 km'''. The minus sign means that the linear eccentricity is negative, and the apogee points towards the sun. |
| Line 52: | Line 51: |
| Perhaps the m360 and m480 orbits should be reserved for lighter and lighter server-sats, assuming that the trend over time will be towards lighter server-sats, better boosters, and more sophisticated latency management. Solar power arrays at lunar distances will be very light, but will have a lot more room for linear eccentricity displacements. | Perhaps the m480 orbit should be reserved for lighter and lighter server-sats, assuming a trend over time towards lighter server-sats, better boosters, and more sophisticated latency management. Solar power arrays at lunar distances will be very light, but will have a lot more room for linear eccentricity displacements. |
| Line 56: | Line 55: |
| The above discussion assumes that the server-sat is under control, and face-forwards towards the sun for maximum power. This is best for computation productivity. However, it is also possible to raise or lower the orbit somewhat by tilting the server-sat at various parts of the orbit. For example, if the server-sat is tilted 60 degrees away from the sun while orbiting towards it (cutting light power and light pressure in half) and face-on towards the sun while orbiting away from it, it will slowly gain orbital speed, about 2cm/sec per orbit, or 42 meters per second per year, raising the orbit. After a few decades, it might be close enough to the moon to either be slingshotted into solar orbit, or sent plunging back to reenter. | The above discussion assumes that the server-sat is under control, and face-forwards towards the sun for maximum power and acceleration. This is best for computation productivity. However, it is also possible to raise or lower the orbit somewhat by tilting the server-sat at various parts of the orbit. For example, if the server-sat is tilted 60 degrees away from the sun while orbiting towards it (cutting light power and light pressure in half) and face-on towards the sun while orbiting away from it, it will slowly gain altitude. After a few decades, it might be close enough to the moon to collide with it, or be sent plunging back to reenter. 100 micron server-sats are thick and heavy compared to "traditional" ultra-thin membrane solar cells. Large orbit changes will be very slow. MORE LATER |
Light Pressure Modified Orbits
Light pressure effects modify server-sat array orbits. In the nominal orbit, server-sats are at "half thrust", with each thruster half mirror and half transparent. Variations to full or zero reflectivity, and full or zero thrust, allow each server-sat to maneuver in relation to the array, or for the array as a whole to maneuver around its assigned centerpoint. The following is an analysis of two effects, earth oblateness and nominal half-thrust light pressure, on the orbit. We will assume that the arrays maintain a constant, slightly elliptical orbit that precesses once per year in the equatorial plane. We will assume continuous illumination tangential to the equatorial plane, and zero light pressure effects from Earth albedo or black-body radiation, and no solar or lunar tides. These assumptions are somewhat crude approximations to get us into the ballpark of a solution. Precise solutions will probably demand accurate numerical solutions simulating many years of orbital evolution.
Earth Oblateness
For "heavy" server-sats relatively close to the earth, such as 7 gram satellites at m288, the dominant deviation from a perfect Kepler orbit is caused by the "J2" spherical harmonic of the gravity field, in turn caused by the oblateness of the spinning Earth. For small eccentricities, the J2 term of the WGS84 model ( -1.082626683E-03 , see Pisacane 2008 ), times the inverse of the orbit radius squared, scales the eastward precession of the perigee of an elliptical equatorial orbit. The precession, expressed as the number complete precessions per year, is J \approx -3 J_2 ( Y / P ) ( R_e / R_s ) ^ 2 where J \equiv precessions per year caused by oblateness, J_2 \equiv spherical harmonic of gravity causing oblateness, Y \equiv year period in seconds, P \equiv orbit period in seconds, Y/P \equiv number of orbits per year, R_e \equiv earth equatorial radius = 6378km, R_s \equiv orbit equatorial radius.
orbit |
radius (RE) |
orbits/year |
J |
LEO |
1.047 |
5758.5 |
17.061 |
m288 |
2.005 |
2191.5 |
1.771 |
m360 |
2.264 |
1826.2 |
1.157 |
m480 |
2.627 |
1461.0 |
0.688 |
m720 |
3.182 |
1095.7 |
0.351 |
m1440 |
4.168 |
730.5 |
0.137 |
GEO |
6.611 |
365.2 |
0.027 |
An orbit that always appears in the same spot in the sky at the same time every day is logistically simpler. It would precess once per year. As we will see, light pressure causes an eccentric orbit with apogee towards the sun to precess retrograde ( negative ) per year, while an orbit with perigee towards the sun precesses prograde (positive). We make up the differece, plus or minus, with light pressure. For orbits like m360, the light pressure effects on precession must be small to make up the small difference, requiring high-mass server-sats or large eccentricity orbits. Perhaps m360 should be reserved for high mass satellites like the O3B constellation.
Light Pressure
|
Solar light pressure is useful for maneuvering, but it distorts orbits. Light pressure slows objects orbiting towards the sun, and speeds up objects orbiting away from it. This raises and lowers portions of the orbit. A slightly elliptical orbit with perigee towards the sun will precess prograde, while an orbit with apogee towards the sun will precess retrograde. With proper matching of eccentricity, and added to the J2 precession the apogee and perigee will complete one precession per year. |
|
An orbit can be viewed in a rotating frame of reference centered on a point in circular orbit. For small eccentricities, an elliptical orbit traces a circle in this frame, rotating in the opposite direction from the orbit itself. That is, if the orbit is eastwards, rotating counterclockwise when viewed from the north, the orbit rotates clockwise in the rotating frame. If the frame is positioned with the earth below, the top of the circle is the apogee and the bottom of the circle is the perigee, so the orbit moves backwards (to the right) compared to the "circular center" at apogee (more slowly), and forwards (to the left) at perigee (more rapidly). |
Ignoring the J_2 spherical harmonic, if the orbit precesses once per year, then the vector of the linear eccentricity makes one complete rotation per year. Each orbit adds a little bit of rotation to that vector, and that little bit of rotation is the sum of the light pressure and the J2 perturbations.
Viewed closely, the displacement caused by light pressure looks like a cycloid ruffle on the orbit circle. In the rotating frame of reference, the sun appears to rotate around the orbit circle once per orbit period, with the light pressure acceleration pointing away from the sun. The sun "disappears" during the eclipsed part of the orbit, and this changes the math somewhat, but the major effects are caused when the object is moving towards or away from the sun, on the sides of the ellipse. This rough estimate ignores eclipses.
Referenced to a zero angle at apogee, the light pressure acceleration in the x direction is a_x = a_L sin( \omega t ) and a_y = a_L cos( \omega t ) . a_L is approximately 17 \mu m / s ^ 2 for a 100 micron thick server-sat. Starting at zero position and velocity, then doubly integrating each of these equations results in \Delta x = ( a_L / \omega^2 ) ( \omega t - sin ( \omega t ) ) and \Delta y = ( a_L / \omega^2 ) ( 1 - cos ( \omega t ) ) . This is the formula for a cycloid. After one orbit period P ( \omega = 2 \pi / P ) \Delta x has shifted by a_L P^2 / 2 \pi . The sum of these increments, plus J, add up to the orbit circle over one year Y, so \Delta x Y / P = 2 \pi ( 1 - J ) \epsilon r_0 . Solving for the linear eccentricity, \epsilon r_0 = ( a_L P Y )/( 1 - J ) (2 \pi)^2 ). For a_L = 17 \mu m / s ^ 2 and the m288 orbit ( P = 4*3600 = 14400 seconds, J = 1.771 ) and a year of 31556926 seconds, this is approximately -250 km. The minus sign means that the linear eccentricity is negative, and the apogee points towards the sun.
Lighter server-sats will have higher light pressure acceleration, and orbit with larger linear eccentricities. This will result in larger relative displacements. Regions of m288 with higher and lower server-sat area-to-mass ratios should be separated by hundreds or thousands of kilometers.
Perhaps the m480 orbit should be reserved for lighter and lighter server-sats, assuming a trend over time towards lighter server-sats, better boosters, and more sophisticated latency management. Solar power arrays at lunar distances will be very light, but will have a lot more room for linear eccentricity displacements.
Orbital Decay or Expansion
The above discussion assumes that the server-sat is under control, and face-forwards towards the sun for maximum power and acceleration. This is best for computation productivity. However, it is also possible to raise or lower the orbit somewhat by tilting the server-sat at various parts of the orbit. For example, if the server-sat is tilted 60 degrees away from the sun while orbiting towards it (cutting light power and light pressure in half) and face-on towards the sun while orbiting away from it, it will slowly gain altitude. After a few decades, it might be close enough to the moon to collide with it, or be sent plunging back to reenter.
100 micron server-sats are thick and heavy compared to "traditional" ultra-thin membrane solar cells. Large orbit changes will be very slow. MORE LATER
Over a very long time, tumbling and completely out of control, random variations in up and down orbit acceleration would eventually drive it up and down, probably in something resembling a random walk. This process is likely to be very slow.
MORE LATER