Differences between revisions 1 and 24 (spanning 23 versions)

Near Circular Orbits

MORE LATER add pointers to orbit discussions

General Elliptical Orbits

In the orbital plane, neglecting the J_2 spherical oblateness parameter :

gravitational parameter	\large \mu = a^3 \omega^2 = G M
semimajor axis	\large a = \sqrt[3]{ \mu / \omega^2 }
angular velocity	\large \omega = \sqrt{ \mu / a^3 }
sidereal period	\large T = 2\pi / \omega = 2\pi \sqrt{ a^3/\mu }
eccentricity	\large e = ( r_a - r_p ) / ( r_a + r_p )
velocity	\large v_0 = \sqrt{ \mu / ( a (1 - e^2) ) }
true anomaly orbit angle from focus	\Large \theta
eccentric anomaly ellipse center angle	\large E = \Large { { e+\cos(\theta) } \over { 1+e\cos(\theta)}}		periapsis	apoapsis
mean anomaly,	\large M = E - e \sin( E )	earth	perigee	apogee
time from perigee	\large t = M / \omega	sun	perihelion	apohelion
radius	\large r=a\Large{{1-e^2}\over{1+e\cos(\theta)}}	\huge\rightarrow	\large r_p =( 1-e )a	\large r_a =( 1+e )a
perpendicular velocity	\large v_{\perp}= v_0 ( 1+e \cos( \theta ))	\huge\rightarrow	\large v_p =(1+e)v_0	\large v_a =(1-e)v_0
radial velocity	\large v_r = e v_0 \sin( \theta )
total velocity tangent to orbit	\Large v=\LARGE \sqrt{{{2\mu}\over{r}}-{{\mu}\over{a}}}
orbit energy parameter	\large C_3 = \mu / a

Fictional Forces in Orbit

In the rotating frame of a circular orbit, counterclockwise viewed from above the orbital plane, the directions are

direction	unit vector	description
x	\vec i	Tangential to (along the line of) the orbit, in the orbital plane, pointing clockwise or westward
y	\vec j	Radially outwards from the center of rotation, in the orbital plane
z	\vec k	Perpendicular to the orbital plane, northwards

The rotation is expressed as \vec \Omega = \omega \hat k , where \omega is the angular velocity of the orbit . The radial vector \vec r is composed of \vec r = x \vec i + y \vec j + z \vec k .

Coriolis acceleration: \Large \vec a_{Coriolis} = -2 \vec \Omega \times \dot { \vec r }

Centrifugal acceleration: \Large \vec a_{Centrifugal} = - \vec \Omega \times \vec \Omega \times \vec r

FROM HERE DOWN, WORK IN PROGRESS, NOT VERIFIED:

Centripedal (gravity) acceleration: \Large \vec a_{Centripedal} = \omega^2 ( 2 y \vec k - x \vec i - z \vec j )

In scalar equations:

\LARGE \ddot x = -2 \omega \dot y - \omega^2 x

\LARGE \ddot y = 2 \omega \dot x + 3 \omega^2 y

\LARGE \ddot z = -\omega^2 z

Locus of Elliptical Orbit Position in Rotating Frame

Periods of M orbits

M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead. For server sky, these are integer fractions of a 1440 minute synodic day; this makes it easier to calculate the sky position given the orbital parameters and the time of day. the M288 orbit returns to the same apparent position 5 times per day, or 365.256...*5 times per year. That position moves around the earth 365.256...+1 times per year. So the total number of orbits per year, relative to the stars, is 365.256...*6+1 orbits per year. That is divided into the year length in seconds to yield the

Sidereal orbit time = ( 365.256... * 86400 ) / ( 365.256... * 6 + 1 ) = 86400 / ( 6 + 1/365.256... ) = 14393.43227 seconds

1 year = 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds

Note: The following table uses the classic formula \omega^2 a^3 = \mu from the books, and does not take into account the oblate spheroid shape of the Earth, which adds centripedal force for low orbits and thus should increase \omega and | C_3 | . So please check these numbers.

The eccentricities for the M orbits assume orbits mapped onto a 50km minor radius toroid.

symbol		LEO 300Km	M288	M360	GEO	Moon	Earth	units
\mu	gravitation param.	3.98600448E+14					1.3271244E+20	m³/s²
	relative to	earth	earth	earth	earth	earth	Sun
a_g	gravity	8.938095E+00	2.437062E+00	1.911369E+00	2.242078E-01	2.697573E-03	5.930053E-03	seconds
T	sidereal period	5431.009959	14393.432269	17270.543331	86164.099662	2360591.57743	31558149.7635	seconds
T_s	synodic period	5431.944772	14400.000000	17820.000000	86400.000000	2551442.90000	31558149.7635	seconds
T/2\pi	Sidereal / 2pi	864.372081	2290.785853	2748.692283	13713.440926	375698.721205	5022635.5297	seconds
\omega	Angular velocity	1.1569092E-03	4.3653142E-04	3.6380937E-04	7.2921159E-05	2.6617072E-06	1.9909866E-07	rad/sec
	orbits/year	5810.73318	2192.53822	1827.28185	366.25640	13.36879	1.00000
a	semimajor axis	6678000.00	12788970.60	14440980.32	42164169.86	384399000.00	149598261000	meters
R_a	apogee radius	6678000.00	12838970.60	14490980.32	42164169.86	405696000.00	152098232000	meters
R_p	perigee radius	6678000.00	12738970.60	14440980.32	42164169.86	363104000.00	147098290000	meters
e	eccentricity	0.000000	0.001951	0.001728	0.000000	0.055401	0.016711
V_0	mean velocity	7725.84	5582.79	5253.76	3074.66	1023.16	29784.81	m/s
V_a	apogee velocity	7725.84	5571.90	5244.68	3074.66	966.47	29287.07	m/s
V_p	perigee velocity	7725.84	5593.68	5262.84	3074.66	1079.84	30282.55	m/s
C_3	orb. specific energy	-59688596.59	-31167516.16	-27602035.26	-9453534.82	-1036944.55	-887125553	J/kg

-  ⇤ ← Revision 1 as of 2011-03-31 19:44:52 → 
  Size: 1343
  Editor: KeithLofstrom
  Comment:
+   ← Revision 24 as of 2011-04-01 23:55:11 → ⇥
  Size: 7560
  Editor: KeithLofstrom
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 3:
+----
MORE LATER add pointers to orbit discussions
-----
== General Elliptical Orbits ==
-Line 4:
+Line 8:
-MORE LATER add pointers to orbit discussions
+In the orbital plane, neglecting the $ J_2 $ spherical oblateness parameter :
-Line 6:
+Line 10:
-||  symbol   ||                  ||   m288     ||   m360   ||  GEO       || Moon || Earth     || unit     ||
||  $ a $    || semimajor axis   || 1,2788,866 ||          || 42,164,170 ||      ||           || meters   ||        
||  $ r $    || radius           ||  varies    ||  varies  || 42,164,170 || varies || varies || meters   ||
||  $ r_a $  || apogee radius    ||  varies    ||  varies  || 42,164,170 ||  || meters ||
||  $ r_p $  || perigee radius   ||  varies    ||  varies  || 42,164,170 || meters ||
||  $ T $    || sidereal period  ||
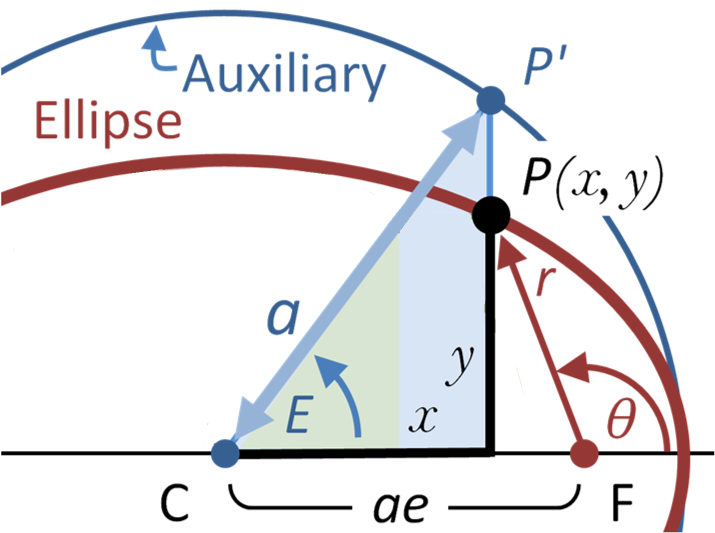
+|| gravitational parameter                 || $ \large \mu = a^3 \omega^2 = G M                 $ ||<|7-3>{{attachment:Anomaly.png|Anomaly|width=400}}||
|| semimajor axis                          || $ \large a   = \sqrt[3]{ \mu / \omega^2 }         $ ||
|| angular velocity                        || $ \large \omega = \sqrt{ \mu / a^3 }              $ ||
|| sidereal period                         || $ \large T = 2\pi / \omega = 2\pi \sqrt{ a^3/\mu }$ ||
|| eccentricity                            || $ \large e = ( r_a - r_p ) / ( r_a + r_p )        $ ||
|| velocity                                || $ \large v_0 = \sqrt{ \mu / ( a (1 - e^2) ) }     $ ||
|| true anomaly<<BR>>orbit angle from focus|| $ \Large \theta                                   $ ||
|| eccentric anomaly<<BR>>ellipse center angle||$\large E = \Large { { e+\cos(\theta) } \over { 1+e\cos(\theta)}}$|| || periapsis  || apoapsis  ||
|| mean anomaly,                           || $ \large M = E - e \sin( E )               $||<)> earth || perigee            ||   apogee       ||
|| time from perigee                       || $ \large t = M / \omega                    $||<)>   sun || perihelion           ||   apohelion    ||
|| radius              || $\large r=a\Large{{1-e^2}\over{1+e\cos(\theta)}}$||<:>$\huge\rightarrow$||$ \large r_p =( 1-e )a $||$ \large r_a =( 1+e )a $||
|| perpendicular velocity || $\large v_{\perp}= v_0 ( 1+e \cos( \theta )) $||<:>$\huge\rightarrow$||$ \large v_p =(1+e)v_0 $||$ \large v_a =(1-e)v_0 $||
|| radial velocity                         || $ \large v_r = e v_0 \sin( \theta )               $||
|| total velocity<<BR>>tangent to orbit    || $ \Large v=\LARGE \sqrt{{{2\mu}\over{r}}-{{\mu}\over{a}}}$||
|| orbit energy parameter                  || $ \large C_3 = \mu / a                            $||
-Line 13:
+Line 26:
-$ r = (1-e^2) a
+----
=== Fictional Forces in Orbit ===
-Line 15:
+Line 29:
------
== Periods of M orbits ==
+In the rotating frame of a circular orbit, counterclockwise viewed from above the orbital plane, the directions are 
|| direction  || unit vector || description                                                                                       ||
|| $ x $      || $ \vec i $  || Tangential to (along the line of) the orbit, in the orbital plane, pointing clockwise or westward ||
|| $ y $      || $ \vec j $  || Radially outwards from the center of rotation, in the orbital plane                               ||
|| $ z $      || $ \vec k $  || Perpendicular to the orbital plane, northwards                                                    ||
-Line 18:
+Line 35:
-M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead.  For server sky, these are integer fractions of a 1440 minute day; this makes it easier to calculate the sky position given the orbital parameters and the time of day.  the M288 orbit returns to the same position 5 times per day, for example, and makes approximately six orbits in the time the earth turns once.  But not exactly.  Because the earth orbits around the sun, the position of the sun makes a complete turn around the earth in one year, 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds
+The rotation is expressed as $ \vec \Omega = \omega \hat k $, where $ \omega $ is the angular velocity of the orbit .  
The radial vector $ \vec r $ is composed of $ \vec r = x \vec i + y \vec j + z \vec k $.

Coriolis acceleration:              $ \Large \vec a_{Coriolis}    = -2 \vec \Omega \times \dot { \vec r } $

Centrifugal acceleration:           $ \Large \vec a_{Centrifugal} = -  \vec \Omega \times \vec \Omega \times \vec r $


FROM HERE DOWN, WORK IN PROGRESS, NOT VERIFIED:

Centripedal (gravity) acceleration: $ \Large \vec a_{Centripedal} =  \omega^2 ( 2 y \vec k - x \vec i - z \vec j ) $

In scalar equations:

   

$ \LARGE \ddot x = -2 \omega \dot y -   \omega^2 x $

$ \LARGE \ddot y =  2 \omega \dot x + 3 \omega^2 y $

$ \LARGE \ddot z = -\omega^2 z $

----
=== Locus of Elliptical Orbit Position in Rotating Frame ===



----
=== Periods of M orbits ===

M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead.  For server sky, these are integer fractions of a 1440 minute synodic day; this makes it easier to calculate the sky position given the orbital parameters and the time of day.  the M288 orbit returns to the same apparent position 5 times per day, or 365.256...*5 times per year.  That position moves around the earth 365.256...+1 times per year.  So the total number of orbits per year, relative to the stars, is 365.256...*6+1 orbits per year.  That is divided into the year length in seconds to yield the

Sidereal orbit time = ( 365.256... * 86400 ) / ( 365.256... * 6 + 1 ) = 86400 / ( 6 + 1/365.256... ) = 14393.43227 seconds

----
1 year = 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds

----
Note:  The following table uses the classic formula $ \omega^2 a^3 = \mu $ from the books, and does not take into account the oblate spheroid shape of the Earth, which adds centripedal force for low orbits and thus should increase $ \omega $ and $ | C_3 | $.  So please check these numbers.

The eccentricities for the M orbits assume orbits mapped onto a 50km minor radius toroid.

||   symbol   ||                      || LEO 300Km     || M288          || M360          || GEO           || Moon          || Earth         ||   units   ||
|| $ \mu $    || gravitation param.   ||<:-5>                 3.98600448E+14                                               || 1.3271244E+20 || m^3^/s^2^ ||
||            ||<)>      relative to  || earth         || earth         || earth         || earth         || earth         || Sun           ||           ||
|| $ a_g $    || gravity              || 8.938095E+00  || 2.437062E+00  || 1.911369E+00  || 2.242078E-01  || 2.697573E-03  || 5.930053E-03  || seconds   ||
|| $ T $      || sidereal period      || 5431.009959   || 14393.432269  || 17270.543331  || 86164.099662  || 2360591.57743 || 31558149.7635 || seconds   ||
|| $ T_s $    || synodic period       || 5431.944772   || 14400.000000  || 17820.000000  || 86400.000000  || 2551442.90000 || 31558149.7635 || seconds   ||
|| $ T/2\pi $ || Sidereal / 2pi       || 864.372081    ||  2290.785853  ||  2748.692283  || 13713.440926  || 375698.721205 ||  5022635.5297 || seconds   ||
|| $ \omega $ || Angular velocity     || 1.1569092E-03 || 4.3653142E-04 || 3.6380937E-04 || 7.2921159E-05 || 2.6617072E-06 || 1.9909866E-07 || rad/sec   ||
||            || orbits/year          || 5810.73318    ||   2192.53822  ||    1827.28185 ||     366.25640 ||     13.36879  ||       1.00000 ||           ||
|| $ a $      || semimajor axis       || 6678000.00    ||  12788970.60  ||  14440980.32  ||  42164169.86  || 384399000.00  || 149598261000  ||  meters   ||
|| $ R_a $    || apogee radius        || 6678000.00    ||  12838970.60  ||  14490980.32  ||  42164169.86  || 405696000.00  || 152098232000  ||  meters   ||
|| $ R_p $    || perigee radius       || 6678000.00    ||  12738970.60  ||  14440980.32  ||  42164169.86  || 363104000.00  || 147098290000  ||  meters   ||
|| $ e $      || eccentricity         || 0.000000      ||  0.001951     ||  0.001728     ||  0.000000     ||  0.055401     ||    0.016711   ||           ||
|| $ V_0 $    || mean velocity        ||  7725.84      ||  5582.79      ||  5253.76      ||  3074.66      ||   1023.16     ||    29784.81   ||  m/s      ||
|| $ V_a $    || apogee velocity      ||  7725.84      ||  5571.90      ||  5244.68      ||  3074.66      ||    966.47     ||    29287.07   ||  m/s      ||
|| $ V_p $    || perigee velocity     ||  7725.84      ||  5593.68      ||  5262.84      ||  3074.66      ||   1079.84     ||    30282.55   ||  m/s      ||
|| $ C_3 $    || orb. specific energy || -59688596.59  || -31167516.16  || -27602035.26  || -9453534.82   ||  -1036944.55  || -887125553    ||  J/kg     ||

Diff for "NearCircularOrbits"

Near Circular Orbits

General Elliptical Orbits

Fictional Forces in Orbit

Locus of Elliptical Orbit Position in Rotating Frame

Periods of M orbits