|
Size: 3578
Comment:
|
Size: 7419
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
| ---- MORE LATER add pointers to orbit discussions ----- == General Elliptical Orbits == |
|
| Line 4: | Line 8: |
| MORE LATER add pointers to orbit discussions | In the orbital plane, neglecting the $ J_2 $ spherical oblateness parameter : || gravitational parameter || $ \large \mu = a^3 \omega^2 = G M $ ||<|7-3>{{attachment:Anomaly.png|Anomaly|width=400}}|| || semimajor axis || $ \large a = \sqrt[3]{ \mu / \omega^2 } $ || || angular velocity || $ \large \omega = \sqrt{ \mu / a^3 } $ || || sidereal period || $ \large T = 2\pi / \omega = 2\pi \sqrt{ a^3/\mu }$ || || eccentricity || $ \large e = ( r_a - r_p ) / ( r_a + r_p ) $ || || velocity || $ \large v_0 = \sqrt{ \mu / ( a (1 - e^2) ) } $ || || true anomaly<<BR>>orbit angle from focus|| $ \Large \theta $ || || eccentric anomaly<<BR>>ellipse center angle||$\large E = \Large { { e+\cos(\theta) } \over { 1+e\cos(\theta)}}$|| || periapsis || apoapsis || || mean anomaly, || $ \large M = E - e \sin( E ) $||<)> earth || perigee || apogee || || time from perigee || $ \large t = M / \omega $||<)> sun || perihelion || apohelion || || radius || $\large r=a\Large{{1-e^2}\over{1+e\cos(\theta)}}$||<:>$\huge\rightarrow$||$ \large r_p =( 1-e )a $||$ \large r_a =( 1+e )a $|| || perpendicular velocity || $\large v_{\perp}= v_0 ( 1+e \cos( \theta )) $||<:>$\huge\rightarrow$||$ \large v_p =(1+e)v_0 $||$ \large v_a =(1-e)v_0 $|| || radial velocity || $ \large v_r = e v_0 \sin( \theta ) $|| || total velocity<<BR>>tangent to orbit || $ \Large v=\LARGE \sqrt{{{2\mu}\over{r}}-{{\mu}\over{a}}}$|| || orbit energy parameter || $ \large C_3 = \mu / a $|| ---- === Fictional Forces in Orbit === In the rotating frame of a circular orbit, counterclockwise viewed from above the orbital plane, the directions are || direction || unit vector || description || || $ x $ || $ \vec i $ || Tangential to (along the line of) the orbit, in the orbital plane, pointing clockwise or westward || || $ y $ || $ \vec j $ || Radially outwards from the center of rotation, in the orbital plane || || $ z $ || $ \vec k $ || Perpendicular to the orbital plane, northwards || The rotation is expressed as $ \vec \Omega = \omega \hat k $, where $ \omega $ is the angular velocity of the orbit . The radial vector $ \vec r $ is composed of $ \vec r = x \vec i + y \vec j + z \vec k $. Coriolis acceleration: $ \Large \ddot{\vec r}_{Coriolis} = -2 \vec \Omega \times \dot { \vec r } $ Centrifugal acceleration: $ \Large \ddot{\vec r}_{Centrifugal} = - \vec \Omega \times \vec \Omega \times \vec r $ FROM HERE DOWN, WORK IN PROGRESS, NOT VERIFIED: Centripedal (gravity) acceleration: $ \Large \ddot{\vec r}_{Centripedal} = \omega^2 ( 2 y \vec k - x \vec i - z \vec j ) $ In scalar equations: $ \LARGE \ddot x = -2 \omega \dot y - \omega^2 x $ $ \LARGE \ddot y = 2 \omega \dot x + 3 \omega^2 y $ $ \LARGE \ddot z = -\omega^2 z $ ---- === Locus of Elliptical Orbit Position in Rotating Frame === |
| Line 8: | Line 62: |
| ---- === Periods of M orbits === |
|
| Line 9: | Line 65: |
| M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead. For server sky, these are integer fractions of a 1440 minute synodic day; this makes it easier to calculate the sky position given the orbital parameters and the time of day. the M288 orbit returns to the same apparent position 5 times per day, or 365.256...*5 times per year. That position moves around the earth 365.256...+1 times per year. So the total number of orbits per year, relative to the stars, is 365.256...*6+1 orbits per year. That is divided into the year length in seconds to yield the | |
| Line 10: | Line 67: |
| $ r = (1-e^2) a | Sidereal orbit time = ( 365.256... * 86400 ) / ( 365.256... * 6 + 1 ) = 86400 / ( 6 + 1/365.256... ) = 14393.43227 seconds |
| Line 12: | Line 69: |
| ----- == Periods of M orbits == |
---- 1 year = 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds |
| Line 15: | Line 72: |
| M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead. For server sky, these are integer fractions of a 1440 minute synodic day; this makes it easier to calculate the sky position given the orbital parameters and the time of day. the M288 orbit returns to the same position 5 times per day, for example, and makes six synodic orbits in one synodic day. But not exactly. Because the earth orbits around the sun, the position of the sun makes a complete turn around the earth in one year, 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds | ---- Note: The following table uses the classic formula $ \omega^2 a^3 = \mu $ from the books, and does not take into account the oblate spheroid shape of the Earth, which adds centripedal force for low orbits and thus should increase $ \omega $ and $ | C_3 | $. So please check these numbers. |
| Line 17: | Line 75: |
| || symbol || || LEO 300Km || M288 || M360 || GEO || Moon || Earth || units || || $ \mu $ || gravitation param. || 3.98600448E+14 || 3.98600448E+14 || 3.98600448E+14 || 3.98600448E+14 || 3.98600448E+14 || 1.32712440E+20 || m^3^/s^2^ || || || relative to || earth || earth || earth || earth || earth || Sun || || || $ a_g $ || gravity || 8.938095E+00 || 2.437062E+00 || 1.911369E+00 || 2.242078E-01 || 2.697573E-03 || 5.930053E-03 || seconds || || $ T $ || sidereal period || 5431.009959 || 14393.432015 || 17270.542964 || 86164.090540 || 2360584.685000 || 31558149.763546 || seconds || || $ T_s $ || synodic period || 5445.879572 || 14400.000000 || 17820.000000 || 86400.000000 || 2551442.900000 || 31558149.763546 || seconds || || $ T/2\pi $ || Sidereal / 2pi || 864.372081 || 2290.785853 || 2748.692283 || 13713.440926 || 375698.721205 || 5022635.529703 || seconds || || $ \omega $ || Angular velocity || 1.15690919E-03 || 4.36531419E-04 || 3.63809367E-04 || 7.29211585E-05 || 2.66170722E-06 || 1.99098659E-07 || rad/sec || || || orbits/year || 5810.73318 || 2192.53822 || 1827.28185 || 366.25640 || 13.36879 || 1.00000 || || || $ R $ || semimajor axis || 6678000.00 || 12788970.60 || 14440980.32 || 42164169.86 || 384399000.00 || 149598261000.00 || meters || || $ R_a $ || apogee radius || 6678000.00 || 12838970.60 || 14490980.32 || 42164169.86 || 405696000.00 || 152098232000.00 || meters || || $ R_p $ || perigee radius || 6678000.00 || 12738970.60 || 14440980.32 || 42164169.86 || 363104000.00 || 147098290000.00 || meters || || $ e $ || eccentricity || 0.000000 || 0.001951 || 0.001728 || 0.000000 || 0.055401 || 0.016711 || || || $ V_0 $ || mean velocity || 7725.84 || 5582.79 || 5253.76 || 3074.66 || 1023.16 || 29784.81 || m/s || || $ V_a $ || apogee velocity || 7725.84 || 5571.90 || 5244.68 || 3074.66 || 966.47 || 29287.07 || m/s || || $ V_p $ || perigee velocity || 7725.84 || 5593.68 || 5262.84 || 3074.66 || 1079.84 || 30282.55 || m/s || || $ C_3 $ || orb. specific energy || -59688596.59 || -31167516.16 || -27602035.26 || -9453534.82 || -1036944.55 || -887125553.00 || J/kg || |
The eccentricities for the M orbits assume orbits mapped onto a 50km minor radius toroid. |
| Line 35: | Line 77: |
| || || || LEO 300Km || M288 || M360 || GEO || Moon || Earth || units || || $ \mu $ || gravitation param. ||<:-5> 3.98600448e14 || 1.3271244e20 || m^3^/s^2^ || || ||<)> relative to || earth || earth || earth || earth || earth || Sun || || || $ a_g $ || gravity || 8.938095 || 2.437062 || 1.911369E || 0.02242078 || 0.002697573 || 0.005930053 || s || || $ T $ || sidereal period || 5431.00996 || 14393.4323 || 17270.5433 || 86164.100 || 2360591.577 || 31558149.76 || s || || $ T_s $ || synodic period || 5431.944772 || 14400 || 17820 || 86400 || 2551442.9 || 31558149.76 || s || || $ T/2\pi $ || Sidereal / 2pi || 864.37208 || 2290.78585 || 2748.69228 || 13713.44093 || 375698.7212 || 5022635.5297 || s || || $ \omega $ || Angular velocity || 1.15690e-03 || 4.36531e-04 || 3.63809e-04 || 7.29212e-05 || 2.66171e-06 || 1.99099e-07 || rad/s || || || orbits/year || 5810.7332 || 2192.5382 || 1827.2819 || 366.25640 || 13.36879 || 1.00000 || || || $ a $ || semimajor axis || 6678000 || 12788970.60 || 14440980.32 || 42164169.86 || 384399000 || 1.4959826e11 || m || || $ R_a $ || apogee radius || 6678000 || 12838970.60 || 14490980.32 || 42164169.86 || 405696000 || 1.5209823e11 || m || || $ R_p $ || perigee radius || 6678000 || 12738970.60 || 14440980.32 || 42164169.86 || 363104000 || 1.4709829e11 || m || || $ e $ || eccentricity || 0.000000 || 0.001951 || 0.001728 || 0.000000 || 0.055401 || 0.016711 || || || $ V_0 $ || mean velocity || 7725.84 || 5582.79 || 5253.76 || 3074.66 || 1023.16 || 29784.81 || m/s || || $ V_a $ || apogee velocity || 7725.84 || 5571.90 || 5244.68 || 3074.66 || 966.47 || 29287.07 || m/s || || $ V_p $ || perigee velocity || 7725.84 || 5593.68 || 5262.84 || 3074.66 || 1079.84 || 30282.55 || m/s || || $ C_3 $ || orb. specific energy || -59688597 || -31167516 || -27602035 || -9453535 || -1036945 || -887125553 || J/kg || |
Near Circular Orbits
MORE LATER add pointers to orbit discussions
General Elliptical Orbits
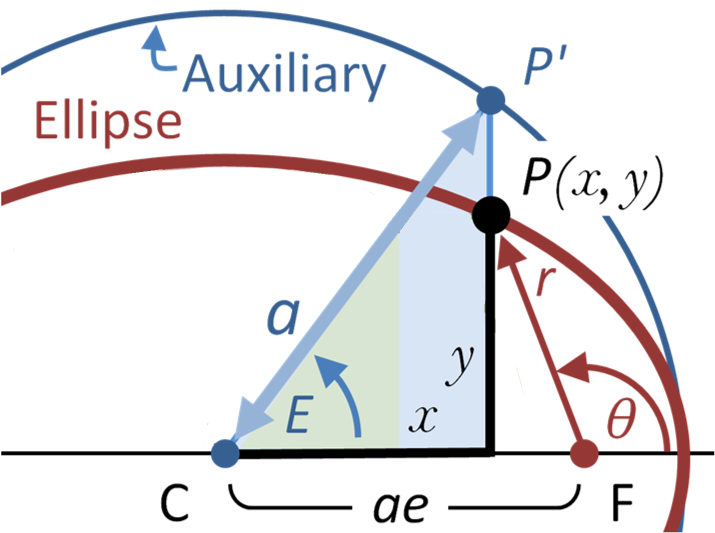
In the orbital plane, neglecting the J_2 spherical oblateness parameter :
gravitational parameter |
\large \mu = a^3 \omega^2 = G M |
|
||
semimajor axis |
\large a = \sqrt[3]{ \mu / \omega^2 } |
|||
angular velocity |
\large \omega = \sqrt{ \mu / a^3 } |
|||
sidereal period |
\large T = 2\pi / \omega = 2\pi \sqrt{ a^3/\mu } |
|||
eccentricity |
\large e = ( r_a - r_p ) / ( r_a + r_p ) |
|||
velocity |
\large v_0 = \sqrt{ \mu / ( a (1 - e^2) ) } |
|||
true anomaly |
\Large \theta |
|||
eccentric anomaly |
\large E = \Large { { e+\cos(\theta) } \over { 1+e\cos(\theta)}} |
|
periapsis |
apoapsis |
mean anomaly, |
\large M = E - e \sin( E ) |
earth |
perigee |
apogee |
time from perigee |
\large t = M / \omega |
sun |
perihelion |
apohelion |
radius |
\large r=a\Large{{1-e^2}\over{1+e\cos(\theta)}} |
\huge\rightarrow |
\large r_p =( 1-e )a |
\large r_a =( 1+e )a |
perpendicular velocity |
\large v_{\perp}= v_0 ( 1+e \cos( \theta )) |
\huge\rightarrow |
\large v_p =(1+e)v_0 |
\large v_a =(1-e)v_0 |
radial velocity |
\large v_r = e v_0 \sin( \theta ) |
|||
total velocity |
\Large v=\LARGE \sqrt{{{2\mu}\over{r}}-{{\mu}\over{a}}} |
|||
orbit energy parameter |
\large C_3 = \mu / a |
|||
Fictional Forces in Orbit
In the rotating frame of a circular orbit, counterclockwise viewed from above the orbital plane, the directions are
direction |
unit vector |
description |
x |
\vec i |
Tangential to (along the line of) the orbit, in the orbital plane, pointing clockwise or westward |
y |
\vec j |
Radially outwards from the center of rotation, in the orbital plane |
z |
\vec k |
Perpendicular to the orbital plane, northwards |
The rotation is expressed as \vec \Omega = \omega \hat k , where \omega is the angular velocity of the orbit . The radial vector \vec r is composed of \vec r = x \vec i + y \vec j + z \vec k .
Coriolis acceleration: \Large \ddot{\vec r}_{Coriolis} = -2 \vec \Omega \times \dot { \vec r }
Centrifugal acceleration: \Large \ddot{\vec r}_{Centrifugal} = - \vec \Omega \times \vec \Omega \times \vec r
FROM HERE DOWN, WORK IN PROGRESS, NOT VERIFIED:
Centripedal (gravity) acceleration: \Large \ddot{\vec r}_{Centripedal} = \omega^2 ( 2 y \vec k - x \vec i - z \vec j )
In scalar equations:
\LARGE \ddot x = -2 \omega \dot y - \omega^2 x
\LARGE \ddot y = 2 \omega \dot x + 3 \omega^2 y
\LARGE \ddot z = -\omega^2 z
Locus of Elliptical Orbit Position in Rotating Frame
Periods of M orbits
M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead. For server sky, these are integer fractions of a 1440 minute synodic day; this makes it easier to calculate the sky position given the orbital parameters and the time of day. the M288 orbit returns to the same apparent position 5 times per day, or 365.256...*5 times per year. That position moves around the earth 365.256...+1 times per year. So the total number of orbits per year, relative to the stars, is 365.256...*6+1 orbits per year. That is divided into the year length in seconds to yield the
Sidereal orbit time = ( 365.256... * 86400 ) / ( 365.256... * 6 + 1 ) = 86400 / ( 6 + 1/365.256... ) = 14393.43227 seconds
1 year = 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds
Note: The following table uses the classic formula \omega^2 a^3 = \mu from the books, and does not take into account the oblate spheroid shape of the Earth, which adds centripedal force for low orbits and thus should increase \omega and | C_3 | . So please check these numbers.
The eccentricities for the M orbits assume orbits mapped onto a 50km minor radius toroid.
|
|
LEO 300Km |
M288 |
M360 |
GEO |
Moon |
Earth |
units |
\mu |
gravitation param. |
3.98600448e14 |
1.3271244e20 |
m3/s2 |
||||
|
relative to |
earth |
earth |
earth |
earth |
earth |
Sun |
|
a_g |
gravity |
8.938095 |
2.437062 |
1.911369E |
0.02242078 |
0.002697573 |
0.005930053 |
s |
T |
sidereal period |
5431.00996 |
14393.4323 |
17270.5433 |
86164.100 |
2360591.577 |
31558149.76 |
s |
T_s |
synodic period |
5431.944772 |
14400 |
17820 |
86400 |
2551442.9 |
31558149.76 |
s |
T/2\pi |
Sidereal / 2pi |
864.37208 |
2290.78585 |
2748.69228 |
13713.44093 |
375698.7212 |
5022635.5297 |
s |
\omega |
Angular velocity |
1.15690e-03 |
4.36531e-04 |
3.63809e-04 |
7.29212e-05 |
2.66171e-06 |
1.99099e-07 |
rad/s |
|
orbits/year |
5810.7332 |
2192.5382 |
1827.2819 |
366.25640 |
13.36879 |
1.00000 |
|
a |
semimajor axis |
6678000 |
12788970.60 |
14440980.32 |
42164169.86 |
384399000 |
1.4959826e11 |
m |
R_a |
apogee radius |
6678000 |
12838970.60 |
14490980.32 |
42164169.86 |
405696000 |
1.5209823e11 |
m |
R_p |
perigee radius |
6678000 |
12738970.60 |
14440980.32 |
42164169.86 |
363104000 |
1.4709829e11 |
m |
e |
eccentricity |
0.000000 |
0.001951 |
0.001728 |
0.000000 |
0.055401 |
0.016711 |
|
V_0 |
mean velocity |
7725.84 |
5582.79 |
5253.76 |
3074.66 |
1023.16 |
29784.81 |
m/s |
V_a |
apogee velocity |
7725.84 |
5571.90 |
5244.68 |
3074.66 |
966.47 |
29287.07 |
m/s |
V_p |
perigee velocity |
7725.84 |
5593.68 |
5262.84 |
3074.66 |
1079.84 |
30282.55 |
m/s |
C_3 |
orb. specific energy |
-59688597 |
-31167516 |
-27602035 |
-9453535 |
-1036945 |
-887125553 |
J/kg |