Near Circular Orbits
General Elliptical Orbits
In the orbital plane, neglecting the J_2 spherical oblateness parameter :
circular orbits |
|
|||
gravitational parameter |
\large \mu = a^3 \omega^2 = G M |
|||
semimajor axis |
\large a = \sqrt[3]{ \mu / \omega^2 } |
|||
angular velocity |
\large \omega = \sqrt{ \mu / a^3 } |
|||
sidereal period |
\large T = 2\pi / \omega = 2\pi \sqrt{ a^3/\mu } |
|||
J_2 Speedup factor |
\large \omega'/\omega = 1+1.5 |J_2| (R_{eq}/a)^2 |
|||
elliptical orbits |
||||
eccentricity |
\large e = ( r_a - r_p ) / ( r_a + r_p ) |
|||
velocity |
\large v_0 = \LARGE\sqrt{\mu\over{a (1 - e^2)}} \large = \LARGE\sqrt{{\mu \over 2}\left({1 \over r_a}+{1 \over r_p}\right)} |
|||
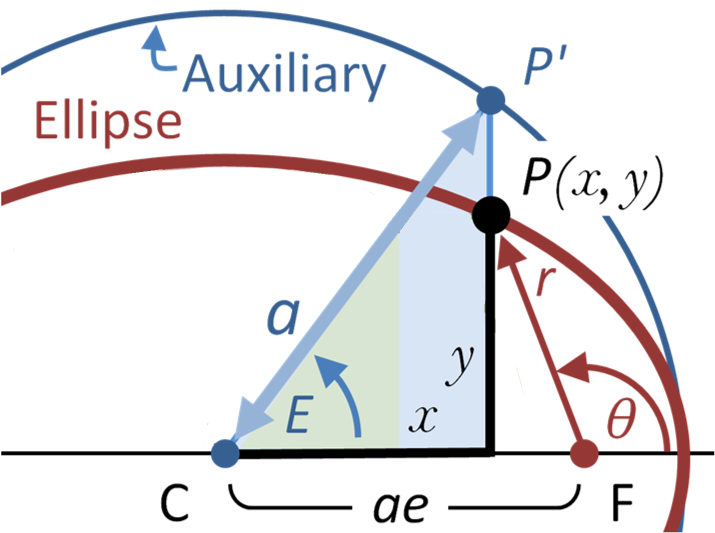
true anomaly |
\Large \theta |
|||
eccentric anomaly |
\large E=\pm\arccos\Large\left({{e+\cos(\theta)}\over{1+e\cos(\theta)}}\right) |
|
periapsis |
apoapsis |
mean anomaly |
\large M = E - e \sin( E ) |
earth |
perigee |
apogee |
time from perigee |
\large t = M / \omega |
sun |
perihelion |
aphelion |
radius |
\large r=a\Large{{1-e^2}\over{1+e\cos(\theta)}} |
\huge\rightarrow |
\large q = r_p =( 1-e )a |
\large Q = r_a =( 1+e )a |
tangential velocity |
\large v_{\perp}= v_0 ( 1+e \cos( \theta )) |
\huge\rightarrow |
\large v_p =(1+e)v_0 |
\large v_a =(1-e)v_0 |
radial velocity |
\large v_r = e v_0 \sin( \theta ) |
\huge\rightarrow |
0 |
0 |
total velocity |
\Large v=\LARGE \sqrt{{{2\mu}\over{r}}-{{\mu}\over{a}}} |
\huge\rightarrow |
\large v=v_p,~ r=r_p |
\large v=v_a,~ r=r_a |
orbit energy parameter |
\large C_3=-\mu/a = -v_p v_a |
\large \mu= a v_p v_a ~~~~~~~~~ 2 a= r_p + r_a |
||
angular momentum |
\large L =\LARGE \sqrt{ { 2 \mu ~ r_a ~ r_p } \over { r_a + r_p } } |
|
\large v_p = \LARGE \sqrt{ { 2 \mu ~ r_a } \over { r_p ( r_a + r_p ) } } |
\large v_a = \LARGE \sqrt{ { 2 \mu ~ r_p } \over { r_a ( r_a + r_p ) } } |
semimajor axis |
\large a={\LARGE{{r_p+r_a}\over{2}}}={\LARGE{{r_p}\over{1-e}}}={\LARGE{{r_a}\over{1+e}}} |
|
\large a = { \LARGE 1 \over { \huge { { 2 \over r_p } - { v_p^2 \over \mu } } } } |
\large a = { \LARGE 1 \over { \huge { 2 \over r_a } - { v_a^2 \over \mu } } } |
semilatus rectum |
\large l = \sqrt{ r_a r_p } |
|
|
|
Computing an orbit from an altitude and a velocity
Assume an Earth orbit, given a radius r and a velocity vector (speed v elevation angle from tangential/horizontal \beta such that the tangential velocity is v_\perp ~ = ~ v \cos( \beta ) ). The vector and the center of the Earth define a plane. Decompose the velocity vector into a radial and a tangential component in that plane. First, we find the semimajor axis:
\large a ~=~ { \huge { 1 \over { { 2 \over r } - { v^2 \over \mu } } } }
Next, compute the angular momentum:
\large L ~=~ r v ~ \cos( \beta )
Compute the eccentricity:
\large e ~=~ \sqrt{ 1 - {\LARGE {{ L^2 } \over { \mu a }} } }
apoapse ~=~ \large ( 1 + e ) a ~~~~~~ periapse ~=~ \large ( 1 - e ) a
Changing perigee by changing apogee velocity
\large v_a^2 = 2 \mu \LARGE \left( { 1 \over r_a } - { 1 \over {r_a + r_p} } \right) ~ ~ ~ ~ ~ ~ \LARGE { { \partial v_a } \over { \partial r_p } } = { \mu \over { v_a ( r_a + r_p )^2 } } ~ ~ ~ ~ ~ ~ for nearly circular orbits: ~ ~ ~ \LARGE { { \partial v } \over { \partial r } } \approx { v \over { 4 r } }
Fictional Forces in Orbit
In the rotating frame of a circular orbit, counterclockwise viewed from above the orbital plane, the directions are
direction |
unit vector |
description |
x |
\vec i |
Tangential to (along the line of) the orbit, in the orbital plane, pointing clockwise or westward |
y |
\vec j |
Radially outwards from the center of rotation, in the orbital plane |
z |
\vec k |
Perpendicular to the orbital plane, northwards |
The rotation is expressed as \vec \Omega = \omega \vec k , where \omega is the angular velocity of the orbit . The radial vector \vec r is composed of \vec r = x \vec i + y \vec j + z \vec k .
Coriolis acceleration: \large \ddot{\vec r}_{Coriolis} = -2 \vec \Omega \times \dot { \vec r }
Centrifugal acceleration: \large \ddot{\vec r}_{Centrifugal} = - \vec \Omega \times \vec \Omega \times \vec r
FROM HERE DOWN, WORK IN PROGRESS, NOT VERIFIED:
- note - these are probably the Hill-Clohessy-Wiltshire equations
Centripedal (gravity) acceleration: \large \ddot{\vec r}_{Centripedal} = \omega^2 ( 2 y \vec k - x \vec i - z \vec j )
Scalar equations:
\large \ddot x = 2 \omega \dot y
\large \ddot y = -2 \omega \dot x + 3 \omega^2 y
\large \ddot z = -\omega^2 z
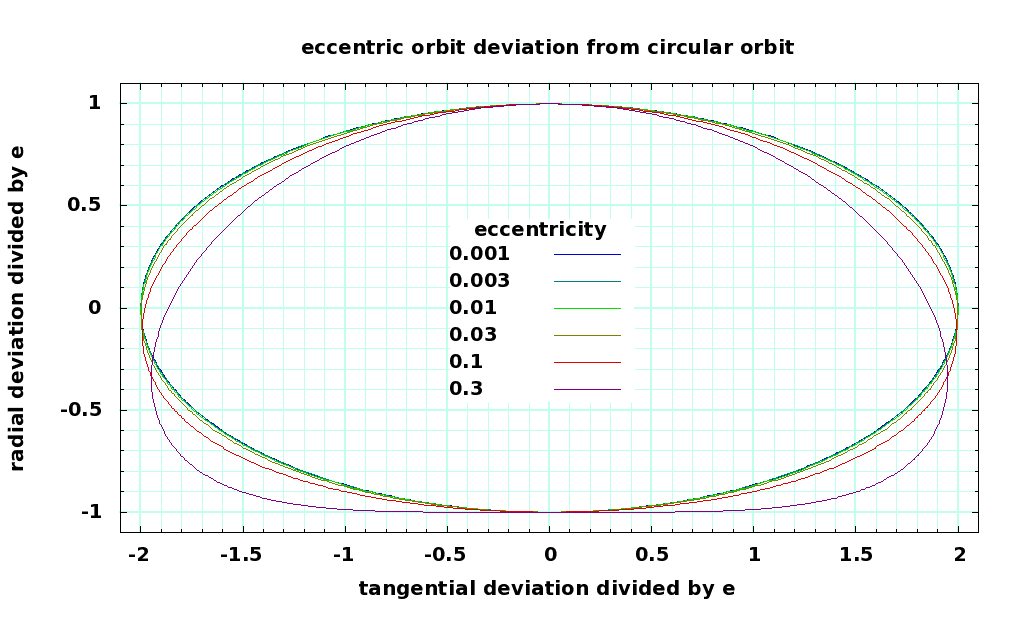
Locus of Elliptical Orbit Position in Rotating Frame
For small eccentricities e, the deviation of the position of an object in a nearly circular eccentric orbit deviates from a ideal circular orbit as an ellipse, with a width of 4e and a height of 2e. This is difficult to compute analytically, but easy to show numerically. Here is a plot the normalized loci of the x,y position in the rotating frame, for various values of eccentricity:
perl data generator locus data gnuplot command file
If the whole orbit rotates east, clockwise when viewed from the north, then the object follows the locus above clockwise, with \theta = 0 at the bottom of the ellipsoid.
The figure is very close to an ellipse for small e, but not exactly so. The program computes the radial distance rr, and the radial position xr and yr as a function of \theta. The program then computes the eccentric anomaly E, and the mean anomaly M. It then rotates the position vector back along the orbit, to approximately vertical, then subtracts the unit vector representing the elliptical orbit. So, it is approximately like watching an object in an elliptical orbit from a position in a circular orbit with the same semimajor axis. The deviation from an ellipse is quite small, until the eccentricity gets larger than 0.01 or so. Server sky orbits will have eccentricities of less than 0.002 .
In the rotating frame, these eccentric loci describe the path of an object subject to fictitious forces. This provides an additional check on our equations for fictitious forces.
The math
\large \dot{ \theta } = v_{\perp} / r = v_0 ( 1+e \cos( \theta )) / ( a (1-e^2) / {1+e\cos(\theta)}
\large \dot{ \theta } = ( \sqrt{ \mu / ( a (1 - e^2) ) } / a ( 1-e^2 ) ) ( 1 + e\cos( \theta ))^2
\large \dot{ \theta } = ( \sqrt{ \mu / ( a^3 (1 - e^2)^3 ) } ( 1 + 2 e \cos( \theta ) + e^2 \cos( \theta )^2 )
for small perturbations, e^2 \approx 0 , so
\large \dot{ \theta } \approx ( \sqrt{ \mu / a^3 } ( 1 + 2 e \cos( \theta ) )
In the rotating frame, \dot{ x } \approx a ( \dot{ \theta } - \omega ) where \omega \equiv \sqrt{ \mu / a^3 } , so
\large \dot{ x } \approx a \sqrt{ \mu / a^3 } ( ( 1 + 2 e \cos( \theta ) - 1 )
\large \dot{ x } \approx 2 e a \omega ( \cos( \theta ) )
Approximating \theta \approx \omega t , we can integrate to get:
\Large x \approx -2 e a \sin( \theta )
\large \dot{ y } = v_r = e v_0 \sin( \theta ) \approx e a \omega \sin( \omega t ) Integrating:
\Large y \approx -e a \cos( \theta )
For small e , these equations in y and x describe the locus calculated above.
Testing the Equations for Acceleration
\large \ddot x ~ ? = ~ \large 2 \omega \dot y
\large \ddot x = { { d^2 } \over { dt^2 } } ( -2 e a \sin( \theta ) ) = { d \over { dt } } ( -2 e a \omega \cos( \theta ) ) = \Large 2 e a \omega^2 \sin ( \theta )
\large 2 \omega \dot y = 2 \omega { d \over { dt } } -e a \cos( \theta ) = \Large 2 e a \omega^2 \sin ( \theta ) . . . equal!
\large \ddot y ~ ? = ~ \large -2 \omega \dot x + 3 \omega^2 y
\large \ddot y = { { d^2 } \over { dt^2 } } ( -e a \cos( \theta ) ) = { d \over { dt } } ( e a \omega \sin( \theta ) ) = \Large e a \omega^2 \cos( \theta )
\large -2 \omega \dot x + 3 \omega^2 y = -2 \omega { d \over { dt } }( -2 e a \sin( \theta ) + 3 \omega^2 ( - e a \cos( \theta ) ) )
\large ~~~~~~~~~~~~~~= 4 e a \omega^2 \cos(\theta) - 3 e a \omega^2 \cos( \theta ) = \Large e a \omega^2 \cos( \theta )~~~ ... equal!
The acceleration equations work!
Periods of M orbits
M orbits describe the number of minutes an orbit takes travel once around the earth and return to the same position overhead. For server sky, these are integer fractions of a 1440 minute synodic day; this makes it easier to calculate the sky position given the orbital parameters and the time of day. the M288 orbit returns to the same apparent position 5 times per day, or 365.256...*5 times per year. That position moves around the earth 365.256...+1 times per year. So the total number of orbits per year, relative to the stars, is 365.256...*6+1 orbits per year. That is divided into the year length in seconds to yield the
M288 sidereal orbit time = ( 365.256... * 86400 ) / ( 365.256... * 6 + 1 ) = 86400 / ( 6 + 1/365.256... ) = 14393.43227 seconds
1 year = 365.256363004 days of 86,400 seconds, or 31558149.7635456 seconds.
J2 speedup fraction = - 3 J_2 ( a_E / a )^2 = 3 \times 1.082626683e-3 \times (6378107m)^2 / a^2 = 1.321245688e11m^2 / a^2
A Table of orbits
|
|
LEO 300Km |
M288 |
M360 |
GEO |
Moon |
Earth |
units |
\mu |
gravitation param. |
3.98600448e14 |
1.3271244e20 |
m3/s2 |
||||
|
relative to |
earth |
Sun |
|
||||
J_2 |
Oblate-ness |
-1.082626683e-3 earth radius = 6378107m |
-6e-7 |
|
||||
\omega'/\omega |
J2 speedup fraction |
2.9627e-3 |
8.0782e-4 |
6.3356e-4 |
7.4318e-5 |
8.9417e-7 |
2e-17 |
|
a_g |
gravity |
8.938095 |
2.437062 |
1.9113693 |
0.02242078 |
0.002697573 |
0.005930053 |
s |
T |
sidereal period |
5431.010 |
14393.4323 |
17270.5433 |
86164.100 |
2360591.577 |
31558149.76 |
s |
T_s |
synodic period |
5431.945 |
14400 |
17820 |
86400 |
2551442.9 |
31558149.76 |
s |
T/2\pi |
Sidereal / 2pi |
864.3721 |
2290.78585 |
2748.69228 |
13713.44093 |
375698.7212 |
5022635.5297 |
s |
\omega |
Angular velocity |
1.1569e-03 |
4.36531e-04 |
3.63809e-04 |
7.29212e-05 |
2.66171e-06 |
1.99099e-07 |
rad/s |
|
orbits/year |
5810.733 |
2192.5382 |
1827.2819 |
366.25640 |
13.36879 |
1.00000 |
|
a |
semimajor axis |
6678000 |
12788971 |
14440980 |
42164170 |
384399000 |
1.4959826e11 |
m |
R_a |
apogee radius |
6678000 |
12838976 |
14440980 |
42164170 |
405696000 |
1.5209823e11 |
m |
R_p |
perigee radius |
6678000 |
12738976 |
14440980 |
42164170 |
363104000 |
1.4709829e11 |
m |
e |
eccentricity |
0.000000 |
0.001951 |
0.001728 |
0.000000 |
0.055401 |
0.016711 |
|
V_0 |
mean velocity |
7725.84 |
5582.79 |
5253.76 |
3074.66 |
1023.16 |
29784.81 |
m/s |
V_a |
apogee velocity |
7725.84 |
5571.90 |
5244.68 |
3074.66 |
966.47 |
29287.07 |
m/s |
V_p |
perigee velocity |
7725.84 |
5593.68 |
5262.84 |
3074.66 |
1079.84 |
30282.55 |
m/s |
C_3 |
orb. specific energy |
-59688597 |
-31167516 |
-27602035 |
-9453535 |
-1036945 |
-887125553 |
J/kg |
Note: This table uses the classic formula \omega^2 a^3 = \mu , and does not take into account the oblate spheroid shape of the Earth, and many other perturbations. However, with the perturbations included, and with good data from ground stations and GPS to establish positions and velocities, we really can compute these numbers to this many decimal places. So while the numbers above are actually far less accurate, they represent the precision of the measurements we will someday compute.
The eccentricities for the M orbits assume orbits mapped onto a 50km minor radius toroid.
LAGEOS 1 and LAGEOS 2 are two slightly lower satellites in inclined but highly circular orbits.
REFS:
http://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion
http://en.wikipedia.org/wiki/Eccentric_anomaly ... where I got the picture, then modified it