|
Size: 9281
Comment:
|
Size: 9303
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 70: | Line 70: |
| {{ nl02pow.png }} | {{ attachment:nl02pow.png }} |
| Line 74: | Line 74: |
| {{ nl02nlp.png }} | {{ attachment:nl02nlp.png }} |
Night Side Maneuvers
We can minimize night light pollution, and advance perigee against light pressure orbit distortion, by turning the thinsat as we approach eclipse. The overall goal is to perform 1 complete rotation of the thinsat per orbit, with it perpendicular to the sun on the day-side of the earth, but turning it by varying amounts on the night side.
Another advantage of the turn is that if thinsat maneuverability is destroyed by radiation or a collision on the night side, it will come out of night side with a slow tumble that won't be corrected. The passive radar signature of the tumble will help identify the destroyed thinsat to other thinsats in the array, allowing another sacrificial thinsat to perform a "rendezvous and de-orbit". If the destroyed thinsat is in shards, the shards will tumble. The tumbling shards ( or a continuously tumbling thinsat ) will eventually fall out of the normal orbit, no longer get J_2 correction, and the thinsat orbit will "eccentrify", decay, and reenter. This is the fail-safe way the arrays will reenter, if all active control ceases.
Maneuvering thrust and satellite power
Neglecting tides, the synodic angular velocity of the m288 orbit is \Large\omega = 4.3633e-4 rad/sec = 0.025°/s. The angular acceleration of a thinsat is 13.056e-6 rad/sec2 = 7.481e-4°/s2 with a sun angle of 0°, and 3.740e-4°/s2 at a sun angle of 60°. Because of tidal forces, a thinsat entering eclipse will start to turn towards sideways alignment with the center of the earth; it will come out of eclipse at a different velocity and angle than it went in with.
If the thinsat is rotating at \omega and either tangential or perpendicular to the gravity vector, it will not turn while it passes into eclipse. Otherwise, the tidal acceleration is \ddot\theta = (3/2) \omega^2 \sin 2 \delta where \delta is the angle to the tangent of the orbit. If we enter eclipse with the thinsat not turning, and oriented directly to the sun, then \delta = 30° .
Three Strategies and a Worst Case Failure Mode
There are many ways to orient thinsats in the night sky, with tradeoffs between light power harvest, light pollution, and orbit eccentricity. If we reduce power harvest, we will need to launch more thinsats to compensate, which makes more problems if the system fails. I will present three strategies for light harvest and nightlight pollution. The actual strategies chosen will be blend of those.
Tumbling
If things go very wrong, thinsats will be out of control and tumbling. In the long term, the uncontrolled thinsats will probably orient flat to the orbital plane, and reflect very little light into the night sky, but in the short term (less than decades), they will be oriented in all directions. This is equivalent to mapping the reflective area of front and back (2 π R2 ) onto a sphere ( 4 &pi R2 ). Light shining onto a sphere of radius R is evenly reflected in all directions uniformly. So if the sphere intercepts π R2 I (intensity) units of light, it scatters e I R2/4 units of light (e is albedo) per steradian in all directions. While we will try to design our thinsats with low albedo ( high light absorption on the front, high emissivity on the back), we can assume they will get sanded down and more reflective because of space debris, and they will get broken into fragments of glass with shiny edges, adding to the albedo. Assume the average albedo is 0.5, and assume the light scattering is spherical for tumbling.
Three design orientations
Upload new attachment "g400.swf"
MAX NLP: Full power night sky coverage, maximum night light pollution
The most power is harvested if the thinsats are always oriented perpendicular to the sun. During the half of their orbit into the night sky, there will be some diffuse reflection to the side, and some of that will land in the earth's night sky. The illumination is maximum along the equator. For the M288 orbit, about 1/6th of the orbit is eclipsed, and 1/2 of the orbit is in daylight with the diffuse (Lambertian) reflection scattering towards the sun and onto the day side of the earth. Only the two "horns" of the orbit, the first between 90° and 150° (6pm to 10pm) and the second between 210° and 270° (2am to 6am) will reflect night into the light sky. The light harvest averages to 83% around the orbit.
This is the worst case for night sky illumination. Though it is tempting to run thinsats in this regime, extracting the maximum power per thinsat, it is also the worst case for eccentricity caused by light pressure, and the thinsats must be heavier to reduce that eccentricity.
MIN NLP: Partial night sky coverage, some night light pollution
This maneuver will put some scattered light into the night sky, but not much compared to perpendicular solar illumination all the way into shadow. In the worst case, assume that the surface has an albedo of 0.5 (typical solar cells with an antireflective coating are less than 0.3) and that the reflected light is entirely Lambertian (isotropic) without specular reflections (which will all be away from the earth). At a 60° angle, just before shadow, the light emitted by the front surface will be 1366W/m2 × 0.5 (albedo) × 0.5 ( cos 60° ), and it will be scattered over 2π steradians, so the illumination per steradian will be 54W/m2-steradian just before entering eclipse.
Estimate that the light pollution varies from 0W to 54W between 90° and 150° and that the average light pollution is half of 54W, for 1/3 of the orbit. Assuming an even distribution of thinsat arrays in the constellation, that is works out to an average of 9W/m2-steradian for all thinsats in M288 orbit.
The full moon illuminates the night side of the equatorial earth with 27mW/m2 near the equator. A square meter of thinsat at 6400km distance produces 9W/64000002 or 0.22 picowatts per m4 times the area of all thinsats. If thinsat light pollution is restricted to 5% of full moon brightness (1.3mW/m2), then we can have 6000 km2 of thinsats up there, at an average of 130 W/m2, or about 780GW of thinsats at m288. That is about a million tons of thinsats.
The orientation of the thinsat over a 240 minute synodic m288 orbit at the equinox is as follows, relative to the sun:
time min |
orbit degrees |
rotation rate |
sun angle |
Illumination |
Night Light |
0 to 60 |
0° to 90° |
0 ~ \Large\omega |
0° |
100% |
0W |
60 to 100 |
90° to 150° |
1 ~ \Large\omega |
0° to 60° |
100% to 50% |
0W to 54W |
100 to 140 |
150° to 210° |
4 ~ \Large\omega |
60° to 300° |
Eclipse |
0W |
140 to 180 |
210° to 270° |
1 ~ \Large\omega |
300° to 0° |
50% to 100% |
54W to 0W |
180 to 240 |
270° to 0° |
0 ~ \Large\omega |
0° |
100% |
0W |
The angular velocity change at 0° takes 250/7.481 = 33.4 seconds, and during that time the thinsat turns 0.42° with negligible effect on thrust or power. The angular velocity change at 60° takes 750/3.74 = 200.5 seconds, and during that time the thinsat turns 12.5°, perhaps from 53.7° to 66.3°, reducing power and thrust from 59% to 40%, a significant change. The actual thrust change versus time will be more complicated (especially with tidal forces), but however it is done, the acceleration must be accomplished before the thinsat enters eclipse.
The average illumination fraction is around 78%.
ZERO NLP: Partial night sky coverage, no night light pollution
In this case, in the night half of the sky the edge of the thinsat is always turned towards the terminator. As long as the thinsats stay in control, they will never produce any nighttime light pollution, because the illuminated side of the thinsat is always pointed away from the night side of the earth. The average illumination fraction is around 68%.
The orientation of the thinsat over a 240 minute synodic m288 orbit at the equinox is as follows, relative to the sun:
time min |
orbit degrees |
rotation rate |
sun angle |
Illumination |
Night Light |
0 to 60 |
0° to 90° |
0 ~ \Large\omega |
0° |
100% |
0W |
60 to 100 |
90° to 150° |
1.5 ~ \Large\omega |
0° to 90° |
100% to 0% |
0W |
100 to 140 |
150° to 210° |
3 ~ \Large\omega |
90° to 270° |
Eclipse |
0W |
140 to 180 |
210° to 270° |
1.5 ~ \Large\omega |
270° to 0° |
0% to 100% |
0W |
180 to 240 |
270° to 0° |
0 ~ \Large\omega |
0° |
100% |
0W |
The average illumination fraction is around 68%.
Power versus angle
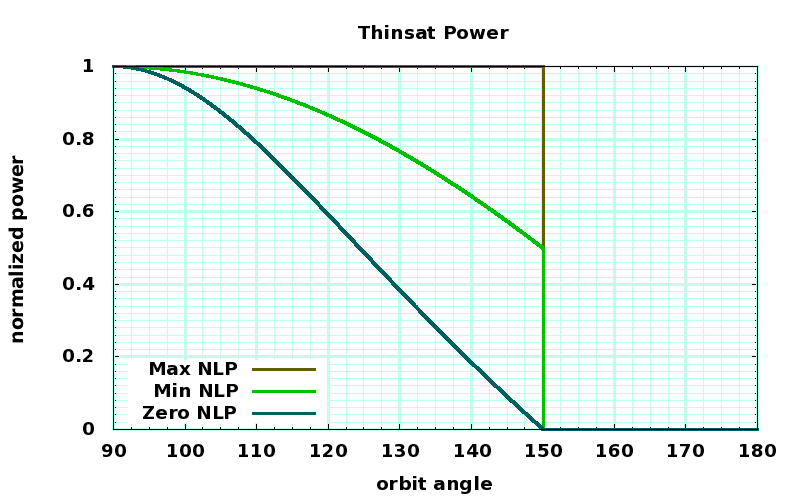
Night light pollution versus hour