|
Size: 7998
Comment:
|
Size: 9468
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 8: | Line 8: |
| The inner belt is mostly created by C.R.A.N.D. - Cosmic Ray Associated Neutron Decay. Cosmic rays striking the upper atmosphere split atoms and generate neutrons with energies above 30MeV. Unbound neutrons have a half-life of 10 minutes and move at more than 10% of the speed of light. The neutrons undergo beta decay and split into an electron, a proton, and an electron antineutrino. 10 minutes at 0.1c is about 20 million kilometers, about 50 times the diameter of the moon's orbit, depositing the particles mostly in that huge volume. The density of these deposited particles falls off as 1/R^2^, so the highest density of these decays occur near the Earth. The electron gets most of the 2MeV beta decay energy, but the proton retains most of the original momentum and energy of the neutron, and have about the same average energy and direction as the original neutron. The electrons are much less massive, so the 2MeV makes them move faster, approaching the speed of light. If the neutron decay occurs in the Earth's magnetic field, and most of the momentum is perpendicular to, rather than parallel to, the magnetic field lines, then the proton spirals around the field lines and gets captured in the Van Allen belt. The likelihood of any neutron decaying within the Van Allen Belt is small - but the small probability is larger in the inner belt, closer to the source. | The inner belt is mostly created by C.R.A.N.D. - Cosmic Ray Associated Neutron Decay. Cosmic rays striking the upper atmosphere split atoms and generate neutrons with energies above 30MeV. Unbound neutrons have a half-life of 10 minutes and move at more than 10% of the speed of light. The neutrons undergo beta decay and split into an electron, a proton, and an electron antineutrino. 10 minutes at 0.1c is about 20 million kilometers, about 50 times the diameter of the moon's orbit, depositing the particles mostly in that huge volume. The density of these deposited particles falls off as 1/R^2^, so the highest density of these decays occur near the Earth. The electron gets most of the 2MeV beta decay energy, but the proton retains most of the original momentum and energy of the neutron, and have about the same average energy and direction as the original neutron. The electrons are much less massive, so the 2MeV makes them move faster, approaching the speed of light. If the neutron decay occurs in the Earth's magnetic field, and most of the momentum is perpendicular to, rather than parallel to, the magnetic field lines, then the proton spirals around the field lines and gets captured in the Van Allen belt. The likelihood of any neutron decaying within the Van Allen Belt is small - but that small probability is larger in the inner belt, closer to the source. |
| Line 10: | Line 10: |
| The outer belt is mostly created by particles captured from the solar wind, which is mostly protons and electrons, but does include some helium and larger nuclei. These particles are less likely to penetrate farther down into the magnetic field, so those solar-sourced particles that do get captured are in the outer belt. | The outer belt is mostly composed of protons and electrons captured from the solar wind, but does include some helium and larger nuclei. In solar storms (flares and coronal mass ejections), the earth's magnetic field is hammered and some of these particles migrate inwards, and a few are pumped up to higher energy. |
| Line 12: | Line 12: |
| Once captured by the magnetic field in either belt, charged particles gyrate around the lines of magnetic field from the earth. Most have some velocity parallel to the field lines, and travel down the field lines as they circle helically around them. The field strength increases as it gets closer to the earth, and this causes the particles to lose perpendicular velocity, then bounce back the other way, at the "mirror point". If the parallel velocity to perpendicular velocity is high enough, the particles collide with the atmosphere before they reach their mirror point, and are taken out of circulation. So only a tiny fraction of source particles become captured electrons and protons, and only a small fraction of those do not collide with the atmosphere. | Once captured by the magnetic field in either belt, charged particles gyrate around the lines of magnetic field from the earth - cyclotron resonance. A 10 MeV proton has a gyroradius of approximately 700 km at 6400 kilometers altitude. Particles have some velocity parallel to the field lines, and travel up and down the field lines as they circle helically around them. The field strength increases as it gets closer to the earth, and this causes the particles to lose perpendicular velocity, then bounce back the other way, at the "mirror point". If the ratio of the parallel velocity to the perpendicular velocity is high enough, the particles will collide with the upper atmosphere before they reach their mirror point, and are taken out of circulation. So only a tiny fraction of source particles become captured electrons and protons, and only a small fraction of those do not collide with the atmosphere. |
| Line 14: | Line 14: |
| But the particles that ''do'' get captured, and "survive infancy", remain in the belts for a long time, some for thousands of years, until they scatter off other particles and increase their ratio of parallel to perpendicular velocity, then drop into the atmosphere. So the generation rates are small, and the recombination rates are small also. | Of the few particles that ''do'' get captured, and "survive infancy", most remain in the belts for a long time, some for thousands of years, until they scatter off other particles and increase their ratio of parallel to perpendicular velocity, then drop into the atmosphere. So the generation rates are small, and the recombination rates are small also. |
| Line 16: | Line 16: |
| The total mass of particles in the entire Van Allen belt is on the order of kilograms. However, the particles are moving very fast and store a lot of energy. Any object in orbit will be hit by only a tiny fraction of them, but the particles that do hit an object may deposit a lot of energy and cause a lot of damage, especially to semiconductor lattices and long-chain organic molecules. | The total mass of particles in the entire Van Allen belt is on the order of [[http://spacemath.gsfc.nasa.gov/weekly/RBSP7.pdf|10 grams]]. However, the particles are moving very fast and store a lot of energy. Any object in orbit will be hit by only a tiny fraction of them, but the particles that do hit an object may deposit a lot of energy and cause a lot of damage, especially to semiconductor lattices and long-chain organic molecules. |
| Line 20: | Line 20: |
| Without a magnetic field, nothing would hold these high energy charged particles near the Earth - they would rapidly dissipate into empty space. So, understanding the magnetic field is essential to understanding how the charged charged particles move. | Without a magnetic field, nothing would hold these high energy charged particles near the Earth - they would rapidly dissipate into empty space. So, understanding the magnetic field is essential to understanding how the charged particles move. |
| Line 22: | Line 22: |
| The Earth's magnetic field is complicated, but to first order, the field can be approximately modelled as a "dipole", similar to a bar magnet with a north and south pole. The dipole is '''not''' conveniently placed at the center of the earth, and is '''not''' lined up with the rotation axis. It is displaced more than 500km north and outwards from the center of the earth, and is tilted about 11 degrees with respect to that center. The center and direction change rapidly over time, causing the north and south magnetic poles to drift about 40 kilometers a year, on random looping trajectories. In 2005, the dipole center was located 552 kilometers from the Earth's center, 22.2 degrees north of the equator (209 kilometers) and 511 kilometers radially outwards from the rotation axis, in the direction of 141.6 east longitude. This spot is between the center of the earth and a point on the Pacific ocean about halfway between Japan and Guam. | The Earth's magnetic field is complicated, but to first order, the field can be approximately modeled as a "dipole", similar to a bar magnet with a north and south pole. The dipole is '''not''' conveniently placed at the center of the earth, and is '''not''' lined up with the rotation axis. It is displaced more than 500km north and outwards from the center of the earth, and is tilted about 11 degrees with respect to that center. The center and direction change over time, causing the north and south magnetic poles to drift about 40 kilometers a year, on random looping trajectories. In 2005, the dipole center was located 552 kilometers from the Earth's center, 22.2 degrees north of the equator (209 kilometers) and 511 kilometers radially outwards from the rotation axis, in the direction of 141.6 east longitude. This spot is between the center of the earth and a point on the Pacific ocean about halfway between Japan and Guam. |
| Line 26: | Line 26: |
| In space, we are not concerned with the poles, or the surface fields, but in the paths of the field lines as they leave the earth's surface in the north and reenter the surface in the south. The field lines follow a path where the radial distance r from the center of the earth is defined by r = L R_e sin ( phi ) ^2^ . phi is the angle from the magnetic dipole axis, so the radial distance is zero in the direction of the north and south magnetic poles, and maximum in the magnetic equatorial plane (which is tilted and displaced from the plane defined by the earth's rotation). R_e is the earth's radius (6378km at the equator) and L is the !McIlwain L-parameter. All the field lines with the same L parameter form a flattened and somewhat distorted torus, called an L-shell. The L=1 shell is mostly within the earth, bulging outwards above the earth over the Pacific, while staying below the surface elsewhere. The L=2 shell extends to 2x6378 or 12756 kilometers from the center of the dipole. Since the dipole is offset by about 400 kilometers, the altitude of the L=2 shell magnetic equator varies between about 5900 and 6900 kilometers above the surface of the earth. | In space, we are not concerned with the poles, or the surface fields, but in the paths of the field lines as they leave the earth's surface in the north and reenter the surface in the south. The field lines follow a path where the radial distance r from the center of the earth is defined by $ r = L R_e \sin( \phi )^2 $. $\phi$ is the angle from the magnetic dipole axis, so the radial distance is zero in the direction of the north and south magnetic poles, and maximum in the magnetic equatorial plane (which is tilted and displaced from the plane defined by the earth's rotation). $R_e$ is the earth's radius (6378km at the equator) and L is the !McIlwain L-parameter. All the field lines with the same L parameter form a flattened and somewhat distorted torus, called an L-shell. The L=1 shell is mostly within the earth, bulging outwards above the earth over the Pacific, while staying below the surface elsewhere. The L=2 shell extends to 2x6378 or 12756 kilometers from the center of the dipole. Since the dipole is offset by about 400 kilometers, the altitude of the L=2 shell magnetic equator varies between about 5900 and 6900 kilometers above the surface of the earth. |
| Line 30: | Line 30: |
| <<EmbedObject(magf05d.swf,play=true,loop=true,width=512,height=384)>> | {{ magf05d.png | | height=384 }} |
| Line 36: | Line 36: |
| The server sky orbit is equatorial, at a radius of 12789km, and the magnetic field is offset compared to it. Over an orbit, the L shell varies like so: | The server sky orbit is equatorial, elliptical with a semimajor axis of 12789km and an eccentricity of 0.0226 (to avoid [[Lageos]]). The perigee radius is 12502km and the apogee radius is 13080km. The magnetic field is offset compared to the orbit. Over an orbit, the L shell varies like so: |
| Line 38: | Line 38: |
| {{attachment:lshell.png|L shell versus orbit angle}} | {{attachment:M288ash.png|L shell versus orbit angle|width=960}} |
| Line 40: | Line 40: |
| [[attachment:ll02.c|ll02.c c source]] . . . [[attachment:ll02.gp|ll02.gp gnuplot commands]] | [[attachment:ll288a.c|ll288a.c c source]] . . . [[attachment:XXXXX3.gp|XXXXX3.gp gnuplot commands]] |
| Line 42: | Line 42: |
| This means that arrays experience slightly different radiation conditions at different parts of their orbit. The orbit "dwells" in the upper and lower L shell extremes, as shown in the histogram. | Arrays experience slightly different radiation conditions at different parts of their orbit. The orbit "dwells" in the upper and lower L shell extremes when these correspond with apogee (local midnight) or perigee (local noon). These extremes occur at 125° west, over the western United States, and western Europe at 0°. Since diffusion between L shells, and magnetic storm distortion, is likely to inject particles at these extremes, these will tend to be higher radiation error regions, requiring more recomputes, and resulting in slower throughput. Fortunately, these regions of the world are already well served by existing compute and fiber optic infrastructure. New and unserved markets in Asia and the western Pacific, from 40° to 150%deg; east, will be in the lowest error regions. Those parts of Asia will be the biggest early market opportunities, By the time Europe, the Western US, and Africa are ready for maximum extra communication and computation, the constellations will be thick enough to Rutherford-scatter all the intersecting L shells, and designs will evolve towards more radiation error resistance and a lower longitude penalty. MoreLater - I need to check my work, the shell animation seems to show the "top bulge" (corresponding to minimum L shell) over Asia. Hmmm --- there goes the business plan. :-( |
| Line 45: | Line 49: |
| === Radiation Dose in 50 micrometer thick glass === | === Radiation Dose in 35 micrometer thick aluminum === |
| Line 47: | Line 51: |
| MORE LATER | MoreLater |
| Line 49: | Line 53: |
| === Rutherford Scattering by Millions of Server Satellites == | === Rutherford Scattering by Millions of Thinsats === |
| Line 51: | Line 55: |
| MORE LATER | MoreLater |
Radiation and the Van Allen Belt
The Particles in the Van Allen Belt
Server Sky arrays in the initial m288 orbit are in the "slot" between the inner and outer Van Allen belts. The radiation is somewhat lower, but still very high. The main difference between the belts is the mechanisms creating them.
The inner belt is mostly created by C.R.A.N.D. - Cosmic Ray Associated Neutron Decay. Cosmic rays striking the upper atmosphere split atoms and generate neutrons with energies above 30MeV. Unbound neutrons have a half-life of 10 minutes and move at more than 10% of the speed of light. The neutrons undergo beta decay and split into an electron, a proton, and an electron antineutrino. 10 minutes at 0.1c is about 20 million kilometers, about 50 times the diameter of the moon's orbit, depositing the particles mostly in that huge volume. The density of these deposited particles falls off as 1/R2, so the highest density of these decays occur near the Earth. The electron gets most of the 2MeV beta decay energy, but the proton retains most of the original momentum and energy of the neutron, and have about the same average energy and direction as the original neutron. The electrons are much less massive, so the 2MeV makes them move faster, approaching the speed of light. If the neutron decay occurs in the Earth's magnetic field, and most of the momentum is perpendicular to, rather than parallel to, the magnetic field lines, then the proton spirals around the field lines and gets captured in the Van Allen belt. The likelihood of any neutron decaying within the Van Allen Belt is small - but that small probability is larger in the inner belt, closer to the source.
The outer belt is mostly composed of protons and electrons captured from the solar wind, but does include some helium and larger nuclei. In solar storms (flares and coronal mass ejections), the earth's magnetic field is hammered and some of these particles migrate inwards, and a few are pumped up to higher energy.
Once captured by the magnetic field in either belt, charged particles gyrate around the lines of magnetic field from the earth - cyclotron resonance. A 10 MeV proton has a gyroradius of approximately 700 km at 6400 kilometers altitude. Particles have some velocity parallel to the field lines, and travel up and down the field lines as they circle helically around them. The field strength increases as it gets closer to the earth, and this causes the particles to lose perpendicular velocity, then bounce back the other way, at the "mirror point". If the ratio of the parallel velocity to the perpendicular velocity is high enough, the particles will collide with the upper atmosphere before they reach their mirror point, and are taken out of circulation. So only a tiny fraction of source particles become captured electrons and protons, and only a small fraction of those do not collide with the atmosphere.
Of the few particles that do get captured, and "survive infancy", most remain in the belts for a long time, some for thousands of years, until they scatter off other particles and increase their ratio of parallel to perpendicular velocity, then drop into the atmosphere. So the generation rates are small, and the recombination rates are small also.
The total mass of particles in the entire Van Allen belt is on the order of 10 grams. However, the particles are moving very fast and store a lot of energy. Any object in orbit will be hit by only a tiny fraction of them, but the particles that do hit an object may deposit a lot of energy and cause a lot of damage, especially to semiconductor lattices and long-chain organic molecules.
Earth's Magnetic Field
Without a magnetic field, nothing would hold these high energy charged particles near the Earth - they would rapidly dissipate into empty space. So, understanding the magnetic field is essential to understanding how the charged particles move.
The Earth's magnetic field is complicated, but to first order, the field can be approximately modeled as a "dipole", similar to a bar magnet with a north and south pole. The dipole is not conveniently placed at the center of the earth, and is not lined up with the rotation axis. It is displaced more than 500km north and outwards from the center of the earth, and is tilted about 11 degrees with respect to that center. The center and direction change over time, causing the north and south magnetic poles to drift about 40 kilometers a year, on random looping trajectories. In 2005, the dipole center was located 552 kilometers from the Earth's center, 22.2 degrees north of the equator (209 kilometers) and 511 kilometers radially outwards from the rotation axis, in the direction of 141.6 east longitude. This spot is between the center of the earth and a point on the Pacific ocean about halfway between Japan and Guam.
The 2006 dipole was tilted by 10.26 degrees from north-south, and further rotated into a plane that is 71.78 degrees west of the prime meridian. This shifts the North geomagnetic pole (the place where the dipole axis surfaces to the north) among the islands north of Canada. The south geomagnetic pole is in Wilkes Land, near the coast of Antarctica and south of Western Australia. The magnetic poles, where the field lines are on average vertical to the earth's surface, are in two other locations.
In space, we are not concerned with the poles, or the surface fields, but in the paths of the field lines as they leave the earth's surface in the north and reenter the surface in the south. The field lines follow a path where the radial distance r from the center of the earth is defined by r = L R_e \sin( \phi )^2 . \phi is the angle from the magnetic dipole axis, so the radial distance is zero in the direction of the north and south magnetic poles, and maximum in the magnetic equatorial plane (which is tilted and displaced from the plane defined by the earth's rotation). R_e is the earth's radius (6378km at the equator) and L is the McIlwain L-parameter. All the field lines with the same L parameter form a flattened and somewhat distorted torus, called an L-shell. The L=1 shell is mostly within the earth, bulging outwards above the earth over the Pacific, while staying below the surface elsewhere. The L=2 shell extends to 2x6378 or 12756 kilometers from the center of the dipole. Since the dipole is offset by about 400 kilometers, the altitude of the L=2 shell magnetic equator varies between about 5900 and 6900 kilometers above the surface of the earth.
The L=1.1 shell and the L=2.0 shells are illustrated in the following animation:
magf05.pov povray source . . . magf05.ini povray control file . . . povinc.tar.gz povray include files
Notice how the 1.1 shell comes very close to the surface over Brazil and the south Atlantic. This causes the South Atlantic Anomaly, where the bottom of the Van Allen Belt comes very close to the surface and low earth orbits get a lot of radiation. The red "poles" indicate the north and south rotational poles, the yellow poles indicate the axis of the inner dipole. The north end of the dipole is tilted towards Canada, and center of the dipole is displaced radially towards Japan.
The server sky orbit is equatorial, elliptical with a semimajor axis of 12789km and an eccentricity of 0.0226 (to avoid Lageos). The perigee radius is 12502km and the apogee radius is 13080km. The magnetic field is offset compared to the orbit. Over an orbit, the L shell varies like so:
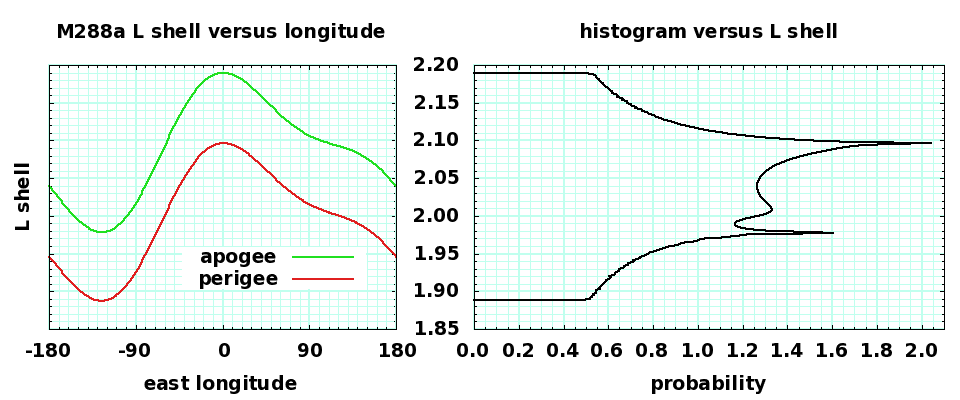
ll288a.c c source . . . XXXXX3.gp gnuplot commands
Arrays experience slightly different radiation conditions at different parts of their orbit. The orbit "dwells" in the upper and lower L shell extremes when these correspond with apogee (local midnight) or perigee (local noon). These extremes occur at 125° west, over the western United States, and western Europe at 0°. Since diffusion between L shells, and magnetic storm distortion, is likely to inject particles at these extremes, these will tend to be higher radiation error regions, requiring more recomputes, and resulting in slower throughput.
Fortunately, these regions of the world are already well served by existing compute and fiber optic infrastructure. New and unserved markets in Asia and the western Pacific, from 40° to 150%deg; east, will be in the lowest error regions. Those parts of Asia will be the biggest early market opportunities, By the time Europe, the Western US, and Africa are ready for maximum extra communication and computation, the constellations will be thick enough to Rutherford-scatter all the intersecting L shells, and designs will evolve towards more radiation error resistance and a lower longitude penalty.
MoreLater - I need to check my work, the shell animation seems to show the "top bulge" (corresponding to minimum L shell) over Asia. Hmmm --- there goes the business plan. ![]()
Radiation Dose in 35 micrometer thick aluminum
