Rutherford Scattering

This analysis must be updated and refined.

Abstract: Server sky thinsats deflect particles in the van Allen belt, and over time cause them to precipitate into the upper atmosphere. 1000 tons of thinsats precipitates 63% of the protons at 1MeV in 20 years ( the electrons much more quickly). The time is inversely proportional to the mass, and proportional to proton energy to the 3/2 power. The process is significant, but far slower than first estimates suggested.

MoreLater

The Details

Thinsats orbit in the van Allen Belt, and encounter very high fluxes of trapped protons and electrons. An array as a whole has a very high surface area to weight ratio. An array of thinsats made of 35 micron thick aluminum has area to mass ratio of 10 m² per kilogram, or 10 km² per thousand metric tonnes (about 200 Ariane launches to m288 ).

When space is populated by a huge area of thinsats, then electrons and protons bouncing back and forth through the L=2 region of the equatorial plane will have a significant chance of encountering the area of the thinsats. Some fraction of those particles will come close to the nuclei of the atoms that make up the aluminum substrate of the thinsats, and they will be scattered. Some particles will change pitch angle, causing the distribution of pitch angle to diffuse and spread out. Particles whose pitch angle decreases enough will move their mirror point (the altitude at which they are reflected by the lower, denser magnetic field) below the top of the atmosphere - those particles will be absorbed. Over time, this reduces the radiation flux in the van Allen belt.

The B field at the equator, L=2, is ( 30 \muT ) / 8 = 3.75 \muT

Define:

• \Large \sigma is area in m²

• \Large \Omega is solid angle in radians²

• \Large e is the electronic charge = 1.60921E-19 Colombs

• \large E_{eV} is the particle energy in electron volts

• \large Z is the atomic number of the target atom

• \Large \epsilon_0 is the permittivity of vacuum = 8.85E-12 Colombs² / Joule-meter

• \Large \theta is the scattering angle

• \large C \LARGE = {{eZ}\over{4\pi\epsilon_0E_{eV}}} ~ ~ is the collision parameter the closest approach for a head-on collision between particle and nucleus.

• \large C_{1MeV} = 1.44E-15 × Z ~ ~ ... in meters

C_{1MeV} is much smaller than the atomic radius (125 picometers for aluminum), the nuclear charge is not shielded by the electron charge of the atoms.

For singularly charged particles like protons and electrons, Rutherford scattering follows the formula:

\large s = (C/2) \cot ( \theta / 2 )

s is the scattering parameter, the distance between the undisturbed trajectory of the incoming particle and the target nucleus, measured in meters. If s is zero, the trajectory runs straight through the nucleus. If s is 1 picometer (a fairly wide miss, actually), then the undisturbed trajectory misses by 1 picometer. But the trajectory is disturbed, and the closest approach is always greater than both s and C.

If s is zero, then \large \theta is \large \pi radians, or 180 degrees. If \theta is 5 degrees, then s is 11.45 C . If \theta is 0, then s is infinite - that is, particles passing far away are not deflected. Practically speaking, the electrons surrounding the nucleus will shield it at distances larger than the atomic radius (which is smaller than the interatomic spacing in the crystal lattice).

We don't care so much about \theta - we care about the component of \theta in the perpendicular direction, or \Delta\alpha . As we will see, that is the perturbation of the pitch angle, which will cause particles to "fall out" of the van Allen belt. That component is \Delta\alpha = \theta \cos ( \phi ) where \phi is the angle between the plane of the deflected particle and the magnetic field line. Our equation becomes:

\large s = ( C / 2 ) \cot ( \Delta\alpha / 2 \cos ( \phi ) )

Let s_x ~ = ~ s ~ cos ( \phi ) and s_y ~ = ~ s ~ sin ( \phi ) . The s_x component is in the direction of the field line. This function can be evaluated between \pm \phi_{max} \equiv \arccos ( \Delta\alpha / \pi ) , and forms a monotonic curve between 0 and \phi_{max} .

If \Delta\alpha is less than 20° ( \phi_{max} \approx 83.6 \deg ), s_x and s_y approximately follow a circular locus with a radius s_0 ~ = ~ ( C / 4 ) \cot ( \Delta\alpha / 2 ) around a center point at ( s_0, 0 ) . This encloses a scattering cross section of:

\large \sigma = \pi s_0^2 = ( \pi C^2 / 16 ) \cot ^2 ( \Delta\alpha / 2 )

For larger \Delta\alpha , the area is reduced, only 95% of the above at 33°, 90% at 52°, and 50% at 142°, reaching 0% at 180°. However, these cross sections are already tiny, and the deflections do not contribute much to the precipitation of particles from the van Allen belt.

The derivative of the cross section with area versus deflection angle (in radians), is the Rutherford Scattering Formula:

\LARGE { { \partial\sigma } \over { \partial\Delta\alpha } } = { { - \pi C^2 ~ \cos ( \Delta\alpha / 2 ) } \over { 16 ~ \sin^3 ( \Delta\alpha / 2 ) } }

Or for small angles (again in radians):

\LARGE { { \partial\sigma } \over { \partial\Delta\alpha } } \approx { { - \pi C^2 } \over { 2 ~ \Delta\alpha ^ 3 } } ~ ~ ~ ... For angles less than 30 degrees, this approximation is accurate to within 0.1%, the 5% error dominates.

Here is a table of scattering angle \large\theta and cross section versus the ratio of impact parameter to collision parameter, s/C :

For Carbon, Oxygen, Aluminum, Silicon, Gold, and SiO₂ glass at 1MeV:

For example, for oxygen atoms with C_{100KeV} = 1.15E-13 meters and an atomic diameter 6.0E-11 meters, then s reaches the atomic diameter when s/C = 520 and \theta = 0.1 degrees . This is a low energy and a small angle, which justifies the "no electrons, nucleus only" assumption.

The Radiation Belts

The energetic particles trapped in the radiation belt spiral helically around magnetic field lines. Their velocity is divided into two components. \large v_{\|}\: is the parallel velocity, along the field line, and \large v_{\bot}\: is the tangential velocity, spiraling around the field line. The radius of the helix is on the order of kilometers. The pitch angle \large \alpha is defined by the ratio of \large v_{\|}\: and \large v_{\bot}\: :

\large \alpha = \normalsize \arctan \Large \left( {{v_{\bot}} \over {v_{\|}}} \right)

If the particle has no parallel velocity, the pitch angle is 90° (or \large\pi/2 radians ). If the particle has only parallel velocity, the pitch angle is zero.

The magnetic field lines are described by the McIlwain model. The field lines close through the inside of the earth, and one might expect particles to follow them to the surface. However, the field intensifies closer to the earth, and this causes the particles to exchange parallel velocity for tangential velocity as they approach the surface, increasing the pitch angle. If the angle reaches 90 degrees before reaching the upper atmosphere, the particle is "mirrored" as shown:

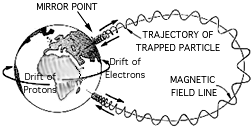
If the particle pitch angle at the equator (defined as \large \alpha_{eq} ) is small enough, it will not accumulate enough pitch angle to mirror, and it will collide with the upper atmosphere and leave the van Allen belt. The particles remaining in the belt have large enough pitch angles to always mirror, unless they are scattered. Define the "loss cone angle" when the particle crosses the magnetic equator (see Piscane equation 6.77 page 150 ):

\large \alpha_{lc} = \normalsize \arcsin \large \left( [ 4{L^6}\:-\:3{L^5} ]^{-0.25} \right) .

Any particles with a loss cone angle less than \large \alpha_{lc} or greater than 180\deg\large\:-\:\alpha_{lc} will fall into the atmosphere.

The m288 orbit is equatorial, and a function of the Earth's rotation axis. The radiation belts, on the other hand, are symmetric to the dipole axis of the magnetic field, which is tilted in relation to the rotation axis. That different parts of the m288 orbit are in different levels (L values) of the magnetic field, and the orbit sweeps out more of the van Allen belt than the width of the m288 constellations themselves. The orbit cuts an annulus through the field.

At m288, the L value varies between 1.93 and 2.14, a band in the equatorial plane between 12310 km and 13650 km from the center of the dipole. This is a disk with an area A_D of 1.1E7 km² . The associated \large \alpha_{lc} values are 17.4° for L=1.93, and 14.6° for L=2.14 . For simplicity, we will assume L=2 and \large \alpha_{lc} = 16°

A scattering event can change the pitch angle, sometimes increasing it, sometimes reducing it. This is why Rutherford scattering by server sky satellites can slowly deplete the van Allen belt, by "diffusing the pitch angle". Thus, a particle with a pitch angle of 20° may be scattered 5° to an angle of 15° and enter the atmosphere.

Assume that the particles bounce from north to south as an approximate sinusoid. They spend more time lingering at the bounce points (at many different latitudes) than they do at the equator; the density of particles is reduced by a factor of 2 / \pi .

If the particles spent all their time near the equator, they would suffer many collisions and be depleted rapidly. If they spend a long time away from the equator, they are less dense where they can collide with thinsats. So the length of their path is proportional to their depletion time.

Their path length is a function of pitch angle and geometry. I don't know the formula for the probability distribution of the pitch angle. However, since we know that particles with pitch angles of the loss cone angle or less are absorbed immediately, we know the probability at those pitch angles is zero, and that the formula is probably symmetric. If we assume removal is a diffusion process, we can guesstimate that the distribution is parabolic, with zeros at the loss cone angle and a maximum at 90°.

Particles with a pitch angle of 90 &deg spend all their time at the magnetic equator, frequently interacting with the thinsats where the magnetic equator crosses the rotation equator, while those at larger pitch angles have longer path lengths.

Let v(E) be the particle velocity at energy E , \sigma(E) be the collision cross section, L( \alpha ) is the path length as a function of pitch angle, and A is the area of the annulus swept out by the thinsats. The collision rate R for a given energy and pitch angle is very approximately:

\Large R ~ \approx ~ \Large { { 2 ~ v(E) ~ \sigma(E) } \over { \pi~ A ~ L( \alpha ) } }

MoreLater

A crude model based on a random walk

Assume that a particle must make an average of 0.5*(90/5)² or about 200 passes at 5 degrees on average to be bounced out - a random walk. We will do a more precise calculation, involving multiple convolutions, after this table. Assume that the maximum s is about half the average SiO₂ atomic size, approximately 1.6E-10 meters.

5 degrees, 1000 tonnes SiO₂ , 200 collisions

The less energetic particles are reduced by 1/e within the lifetime of the server sky satellites, with 1000 metric tons of thinsats in orbit, a population of 300 million first generation thinsats. As we approach 100 billion 0.2 gram satellites, or 20 thousand metric tons, the population decay times go down by a factor of 200. Within a couple of decades, the van Allen belt at server sky altitudes essentially vanishes, with new particles formed from cosmic rays swept out in a few days.

A more accurate calculation

Instead of assuming 5 degrees and a random walk, let's compute the actual diffusion of the initial distribution by computing the convolution of our starting distribution with a probability distribution for scattering versus \Delta\alpha , twice per bounce period.

The probability computed above is for a single scattering center - with tons of thinsats in orbit, there will be many. For scattering angles \Delta\alpha less than 0.1°, temporarily assume no scattering at all. Multiply the rest of the distribution between 0.1° and 30° by the sum of C times N, the collision parameter for each type of atom at a given energy, times the number of those atoms (huge!). Integrate the result, then subtract from one. The remainder is multiplied by a delta impulse function and placed at zero - that is, everything that is not deflected between 0.1° and 30° is assumed to not be deflected. For the actual convolution, we can set the delta to the sum of all the other deflections - whatever is at the zero deflection point is reduced by what is deflected away from it.

Assume both the pitch angle distribution and the deflection probability curve are digitized to 0.1&deg pitch angle accuracy. The pitch angle distribution looks like so:

GRAPH HERE

And the initial deflection probability curve looks like so:

GRAPH HERE

MoreLater