|
⇤ ← Revision 1 as of 2011-01-26 17:58:34
Size: 13123
Comment:
|
Size: 454
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| = Server-sat propulsion, navigation, and orientation = | = Test Page = |
| Line 4: | Line 4: |
| A server-sat is light enough to be significantly accelerated by light pressure. At the earth's distance from the sun, the illumination is 1300 Watts per square meter, on average. The light pressure for absorbed light is the power divided by the speed of light, or about 4E-6 N/m^2^ or 4 microPascal. If the light is reflected, the pressure doubles to 8 microPascal. This is a tiny pressure (sea level atmospheric pressure is 100 kiloPascals) but it is continuous. When pushing on something as thin and light as a server-sat, it can add significant velocity over hours, weeks, and years. The areal density of a 100 micron thick server-sat is 0.233kg/m^2^ , and the albedo of a solar cell is around 0.15, so the acceleration is 1.15x4e-6/0.233 or approximately 20 micrometers/second^2^, or 7 centimeters/minute^2^, or 256 meters/hour^2^. That allows for significant [[ LocalManeuvering | local maneuvering ]]. | 4E-6 N/m^2^ or 4 microPascal. $ F = 3 \omega^2 M L \sin \delta $ where $M$ is the effective mass at distance $L$ with $ {\buildrel..\over\theta}_{max} = (3/2) \omega^2 $ |
| Line 6: | Line 7: |
| Large orbital changes are harder. Server-sats are in orbit, and if they are pointed directly at the sun, they are accelerated directly away from it. That adds to orbital velocity as their orbit takes them away from the sun, but subtracts from orbital velocity as they approach it. If they are tilted in relation to the sun, less area is exposed to light pressure, and the "albedo vector" of reflected light is tilted also, which can add a small sideways thrust. | $ 2/\pi $ |
| Line 8: | Line 9: |
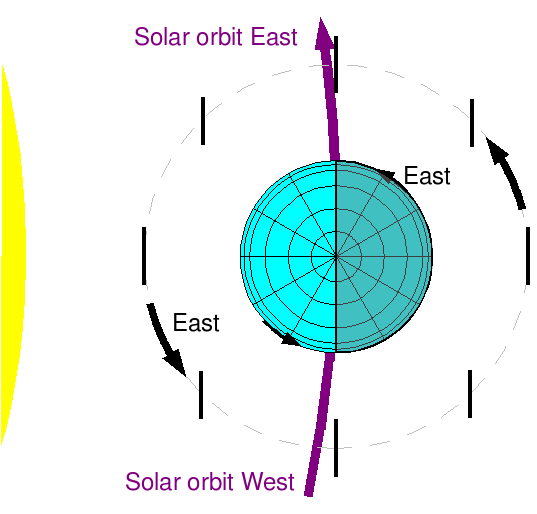
| ||{{attachment:nav_eastwest.png|defining east and west in solar orbit|height=285}}||'''Defining directions'''<<BR>>The earth rotates towards the east, counterclockwise when viewed from the north pole. It makes 366.24 turns relative to the fixed stars per year, and makes 365.24 turns relative to the sun. Orbits launched from earth also travel east, only faster. On the surface of the rotating earth at midnight, east is in the direction of the earth's orbit around the sun, and on the surface of the rotating earth at noon, the earth appears to be moving west. For the sake of argument, we will assume that the '''earth is moving east in its orbit'''. Thus, an object in orbit around the earth is moving towards the sun on the east side of the earth, and away from the sun on the west side of the earth. ''' I may have this backwards compared to some convention, so please add a note and a reference if I goofed this up! '''|| | ||{{attachment:NavigationV01/nav_eastwest.png|defining east and west in solar orbit|height=300}}||<<EmbedObject(NavigationV01/ss5a.swf,play=true,loop=true,width=400,height=300)>>|| |
| Line 10: | Line 11: |
| Server-sats will get the most power if they face directly into the sun. However, they tilt to manuever. and that reduces the thrust. If they are tilted 45 degrees sideways, they get 30% less light and must reduce computing and radio functions, but they will still operate. With a 60 degree tilt, they get half power (and they cool down a lot!). Infrared light from the earth is mostly absorbed by the server-sat, and that creates some light pressure, too. ||{{attachment:light-shift1.png|orbit shifted by light pressure|height=209}}||'''Shifting the orbit center to compensate for light pressure'''<<BR>><<BR>>The perigee and apogee shift outwards approximately 200km, with the light pressure causing this elliptical orbit to precess once per year. See LightOrbit for more details.|| MORE LATER === Light pressure from Optical thrusters === The version 1 design has three round liquid crystal light pressure thrusters at 120 degree angles around the periphery. These are either black or transparent. They are 5cm in diameter (about 2 inches), and have areas of 2e-3 m^2. When reflecting, an ideal thruster produces perhaps 16 nano-Newtons, and when transparent it produces zero. Real materials will always show some reflection in transparent mode, and some transparency in reflective mode . Also, radiation from the earth (both albedo and infrared) reduces the effective thrust. So, the thrust may vary between 12nN and 4nN (WAG). If one thruster on one side is fully reflective, while the other two are clear, the thrusters together produce a torque of 8nN times 10 cm or 800 pico-Newton-meters. If the entire server-sat has a mass of 0.007kg and an average diameter of 8 cm, the angular acceleration is 70 micro-radians per second squared. Accelerating for 36 seconds, then decelerating (applying opposite acceleration) for 36 seconds, will turn the array 10 degrees. Accelerating for 90 seconds, then decelerating for 90 seconds, turns the array approximately 60 degrees (not quite, as the thrusters are moving out of plane and become less effective when turned away from the sun). Here is an animation of a server-sat turning with an angular acceleration of 14 degrees per minute squared ( 70 micro-radians per second squared), for a 56 degree turn in 240 seconds. If your browser renders this flash movie at full speed, it should be running at 10 frames per second, each frame representing 2 seconds, for a 20x speedup over real time. The animation will repeat after 12 seconds. <<EmbedObject(ss5a.swf,play=true,loop=true,width=800,height=600)>> [[ attachment:ss5a.c | Here is the source ]] , and you will need [[ http://www.libgd.org/ | libGD ]] and [[ http://www.swftools.org/ | swftools ]] === Recovering from a spin === Imagine some perturbation like a collision starts the server-sat spinning end over end at 1 revolution per second. Assume that the processors and memory and transmitters go into low power standby mode when this happens, so that power remains for the receivers (for orientation) and for the optical thrusters. The solar cell, when back-lit, will still produce some power, and the capacitors can hold some energy and preserve processor state while the solar cell is precisely edge-on to the sun. The spin is very slow in "computer time" - the server-sat should be able to orient to the sun (crudely) and to other server-sats in the array. However, the tumble will put the server-sat periodically edge-on to the sun, with zero thrust. For an end-over-end tumble, the average thrust is $ 2/\pi $ or 64% of the thrust of the rest of the server-sats in the array - they will be accelerated away from the tumbling server-sat at about 90 meters per hour squared ( (1-0.64)*256m/h2 ). This will rapidly isolate a tumbling server-sat. To recover from a spin, the server-sat will be turning on the reflective optical thrusters on the side moving towards the sun, and turning off the thrusters moving away. The angular acceleration averages out to 50% the peak angular acceleration (both the thrust and the arm distance vary as a rectified sine wave), so the average deceleration is 35 micro-radians per second squared. The rotation (starting at 2 pi radians per second) can be stopped in 180,000 seconds, or about 50 hours. By this time, the tumbling server-sat will be about 110 km from its array, and moving away at 1.3 meters per second. With full-on thrusters providing a delta acceleration of 35 meters per hour squared, or about 3 micrometers per second squared, the isolated server-sat can reduce the relative velocity to zero in about 120 hours, and moves another 280 kilometers further away. Now the server-sat starts moving back to the array, and can return to position in about 200 hours. About half a month to return to position within the array (assuming the isolated server-sat can get close enough to find the array with GPS and other information). While this is inconvenient, the perturbations that start such fast spins are rare. Normal satellites will fail at such impact-generated tumbles. The above discussion assumes "linear" space. Of course, in real orbits the sun angle changes 6 times per day, and velocity changes will change orbits and orbital planes. Objects moving faster in orbit are pushed into a higher orbit with lower period, and drop behind the objects they were formerly arrayed with. So the actual dynamics will be more complicated, but quite computable and will likely operate on slow time scales. {{{#!wiki caution '''Volunteer Opportunities''' <<BR>> Study and simulate the trajectory and recovery of a tumbling server-sat in detail. }}} ||{{attachment:tidal1.png}}||'''Correcting for tidal forces'''<<BR>>At the four "45 degree" points in the orbit, the server-sat is accelerated by tidal forces - the nearer end is pulled inwards by slightly more gravity and slightly less acceleration, and the farther end is pushed outward. These tidal forces are proportional to the vertical distance: $ F = 3 \omega^2 M L \sin \delta $ where $M$ is the effective mass at distance $L$ from the center, $\omega = 2 \pi / Period $ is the angular frequency of the orbit, and $ \delta = \omega t $ is the angle of the disk from the tangent of the orbit. The torque is proportional to the horizontal distance, or $ T = F L \cos \delta = 3 \omega^2 M L^2 \sin \delta cos \delta = (3/2) \omega^2 M L^2 \sin 2 \delta $. <<BR>><<BR>>The orbital angular frequency is $ \omega^2 = \mu / r^3 $ , so the tidal forces diminish rapidly for high orbits.<<BR>><<BR>> The torque and the angular acceleration are maximized at a 45 degree angle. Both the torque and the moment of the server-sat are proportional to $ M L^2 $, so the angular acceleration is $ \buildrel..\over\theta = (3/2) \omega^2 \sin 2 \delta = (3/2) \omega^2 \sin 2 \omega t $ . This can be integrated twice to find the angular displacement from flat towards the sun: $ \theta = \approx -(3/8) \sin 2 \omega t $. The maximum angular displacement is given by $ \theta_{max} \approx \pm 3/8 {\scriptstyle\rm radians} \approx \pm 21.5^\circ $ <<BR>><<BR>> Although this is the "natural" oscillation if the server starts out flat, this is a metastable balance. Other perturbations such as the sun and the moon will eventually displace the server into its lowest energy configuration, which is [[Coplanar | coplanar]] with the orbit. Hence, we will need at least some correction of the orientation.|| Fortunately, the optical thrusters are much more powerful than the tidal forces, and can easily keep the server flat towards the sun. The maximum angular acceleration of the server-sat is $ {\buildrel..\over\theta}_{max} = (3/2) \omega^2 $ or 0.28 micro-radians per second squared for the m288 orbit, while the 5cm thrusters can provide angular accelerations of 70 micro-radians per second squared. This suggests a maximum mass-to-thruster ratio for server-sats: In the m288 orbit, the mass can grow to perhaps 50 grams, or somewhat more with larger thruster area percentage. Keep in mind that much larger thrusters will add more moment as well as more thrust. Since the thrusters will probably degrade over time, a reasonable safety factor is needed as well. In any case, centimeter-thick server-sats are probably out of the question in the m288 orbit, though they might be possible in m720 orbits, with half the angular frequency. === Thrust versus angle === {{ attachment:reflection_thrust.png }} Most of the area of a server-sat is a big solar cell, which absorbs most of the light that hits it. Some portion of the light reflects from the solar cell, and the reflections can be roughly divided into '''diffuse reflections''' (in all directions from the front side) and '''specular reflections''' (opposite the incoming angle, like a good mirror). The diffuse reflections add an effective thrust of about 66% (2/pi) of the diffuse reflected light pressure at the tilt angle of the server-sat, while the specular reflections add a thrust of 100% of the light at twice the tilt angle. Here is a plot of the normalized main thrust ( relative to of power/c, in the direction of the sun) and the side thrust ( normal to the direction of the main thrust ) as a function of tilt from the direction to the sun. The normalized power (relative to max power) is also shown. {{ attachment:reflect01.png }} === Drag and Ballistic Coefficient === The first planned server-sat constellations are in the m288 orbit, at an altitude of 6408 km. The atmosphere is very thin at that altitude, so drag will be negligible. However, server-sats (or fragments of them) may find themselves at lower altitudes, so the [[ballistic_coefficient|ballistic coefficient]] is needed to compute the decay of their orbits. The worst case ballistic coefficient is probably that of a flat plate moving face-on into the airstream, and the best case is edge-on. Lets assume the average resembles a sphere of the same radius (drag coefficient of 2), as it will probably be tumbling end over end. For a 9 cm disk weighing 7 grams, the ballistic coefficent is '''0.15 kg/m^2^''', about 30% of the Echo communication balloon. At the altitude of Teledesic and Globalstar, about 1400km, the mean atmospheric density is around 7.1E-15 kg/m^3^. The decay rate at that altitude will be about 4km/year; the velocity change needed to maintain orbit would be about 4 meters/second/year, or 0.12 microns/second/second. A server-sat can do that, with some maneuvering and perhaps some additional specular albedo added to the sun-side. MORE LATER updated for Version 0.2, half-sized server-sats. |
{{{#! wiki caution '''Test Caution''' }}} |
Test Page
4E-6 N/m2 or 4 microPascal. F = 3 \omega^2 M L \sin \delta where M is the effective mass at distance L with {\buildrel..\over\theta}_{max} = (3/2) \omega^2
2/\pi
|
|
wiki caution '''Test Caution'''