|
Size: 16675
Comment:
|
Size: 18169
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
The temperature of the shell, assuming 1366 W/m^2^ at 1 AU and an emissivity of one, is (1366/5.6704e-8)^1/4^ R^1/2^ or 393.97/&sqrt;R,,au,, Kelvin. || R(au) || T (K) || || 1 || 394.0 || || 2 || 278.6 || || 5 || 176.2 || || 10 || 124.6 || || 20 || 88.1 || || 50 || 55.7 || || 100 || 39.4 || || 200 || 27.9 || Hydrogen sphere freezes || || 500 || 17.6 || || 1000 || 12.4 || 0.0158 light years || |
|
| Line 70: | Line 85: |
| At 0.95 AU, and 5.5 billion years from now, with an expanded solar sphere about 2E6 km in diameter ( 1.4*1.4E6 km ), a shield 5% of the way towards the Sun ( 7.5e6 km sunwards ) must be at least 100,000 kilometers across; assume 200,000 km with a safety factor of 2. A disk of thinsats tracking the earth will feel strong tidal forces. The gravity deflecting the Earth into its circular orbit is $ ~\omega^2 R ~ = ~ ( { { 2 \pi } \over T } )^2 R ~ = ~ $ 5.93 mm/s^2^ . At 0.95 AU, a disk shadowing the earth will see 16% of that, about 0.95 mm/s^2^ ( 9.5e-4 m/s^2^ ) dragging it towards the sun. If the disk is partly reflective, producing about 1e-5 Pa of light pressure (the sun is brighter) then a disk density of about (1e-5/1e-3) or 0.01 kg/m^2^ will balance it. The area of the disk is 3.1E16 m^2^ so the mass is around 3.1E14 kg. That is around 1E11 cubic meters of earth-density rock, about 100 cubic kilometers, the material in a medium-sized asteroid. Such an asteroid could be robotically manufactured into thinsats, which could sent down to a gravity-assist slingshot around the earth, then into the 0.95 AU orbit. | At 0.95 AU, and 5.5 billion years from now, with an expanded solar sphere about 2E6 km in diameter ( 1.4*1.4E6 km ), a shield 5% of the way towards the Sun ( 7.5e6 km sunwards ) must be at least 100,000 kilometers across; assume 200,000 km with a safety factor of 2. A disk of thinsats tracking the earth will feel strong tidal forces. The gravity deflecting the Earth into its circular orbit is $ ~\omega^2 R ~ = ~ ( { { 2 \pi } \over T } )^2 R ~ = ~ $ 5.93 mm/s^2^ . At 0.95 AU, a disk shadowing the earth will see 16% of that, about 0.95 mm/s^2^ ( 9.5e-4 m/s^2^ ) pulling it towards the sun. If the disk is partly reflective, producing about 1e-5 Pa of light pressure (the sun is brighter) then a disk density of about (1e-5/1e-3) or 0.01 kg/m^2^ will balance it. The area of the disk is 3.1e16 m^2^ so the mass (at 50% opacity) is around 1.5e14 kg. That is around 5e10 cubic meters of earth-density rock, about 50 cubic kilometers, the material in a medium-sized asteroid. Such an asteroid could be robotically manufactured into thinsats, which could sent down to a gravity-assist slingshot around the earth, then into the 0.95 AU orbit. Assuming both reflectivity and emissivity of 50% on both front and back (after being scoured by micrometeorites), the black body radiation power on both sides is equivalent to 700W/m^2^ on each side. Assuming isotropic radiation on both sides, the filled area of 1.5e16 m^2^ will emit around 1e19 watts, at a distance of 7.5 million kilometers. If the heat is radiated isotropically, the heat flux on the earth will be 1e19W /( 2 π 7.5e9^2^ m^2^) or 30 mW/m^2^ - negligible compared to the 1366W/m^2^ of sunlight we continue to let through. |
| Line 74: | Line 91: |
| The shield could be a ring of static, hovering thinsats, in the full gravity of the sun, about 6.57 mm/s^2^, or about 6.9 times the gravity of the orbiting disk. That means that for the same light pressure, the ring is 6.9x less dense, 1.45e-3 kg/m^2^. But the ring must extend all the way around the Sun, 8.5E11 meters, for a total area of 1.7E20 m^2^ and a mass of 2.46e17 kg, about 80 times the mass of the orbiting disk, and about 1% of the mass of the asteroids Vesta or Pallas. While this seems more difficult than the orbiting disk, the total energy intercepted would be 4.6E23 watts, about half a trillion terawatts, which could be used for many interesting tasks; communication, computation, propulsion power. | The shield could be a ring of static, hovering thinsats, in the full gravity of the sun, about 6.57 mm/s^2^, or about 6.9 times the acceleration of the orbiting disk. That means that for the same light pressure, the ring is 6.9x less dense, 1.45e-3 kg/m^2^. But the ring must extend all the way around the Sun, 8.5E11 meters, and is 200,000 km across, for a total area of 1.7E20 m^2^ and a mass of 1.2e17 kg, about 80 times the mass of the orbiting disk, and about 1% of the mass of the asteroids Vesta or Pallas. While this seems more difficult than the orbiting disk, the total energy intercepted would be 4.6E23 watts, about half a trillion terawatts, which could be used for many interesting tasks; communication, computation, propulsion power. Assuming the same emissivity as before, 700W/m^2^, the ring will emit 7e10W per meter of length. Divided by a half cylinder distance of 7.5e9 meters, and a half circumference of 2.35e9 meters, that is 3 watts per square meter at the distance of the earth. Much larger than the previous case, but still tiny compared to the 1366W/m^2^ sunlight we are letting though. The result is about the same for the static Venus ring discussed below. |
| Line 80: | Line 99: |
| The total mass of this porous ring is 8E16 kg ( 0.5 * 1.5E3 kg/km^2^ * 108E6 km * 1e6 km ), a tiny fraction of Venus's 4.87E24 kg mass, most of which would be sent out to add (slightly) to the outer shell. The ring would be irradiated with about 5000W/m^2^, and radiate 2500W/m^2^ from each surface, minus the power it radiates as communication energy. The black body temperature of the ring would be 460K. From the earth, the sky be the point source of a dimmed sun, the outer shell at 67K, and 75% of the ring band, 1.76 radians (101 angular degrees) wide and 0.01 radians (0.5 degrees) tall in the middle (42E6 km away) and 0.004 radians (0.22 degrees) tall at the limbs (104E6 km away). The porous band would occupy about 0.011 steradians of the sky. The outer shell would add 1.15 W/m^2^ to the earth's incoming heat, and the band would add 2.2 W/m^2^, (2500W/m^2^ * 0.011 / 4pi ). To keep the Earth at the same temperature as today, we can lower the solar light input by 3.4 W/m^2^ out of 1366 W/m^2^ . | The total mass of this porous ring is 8E17 kg ( 0.5 * 1.5E3 kg/km^2^ * 108E6 km * 1e6 km ), a tiny fraction of Venus's 4.87E24 kg mass, most of which would be sent out to add (slightly) to the outer shell. The ring would be irradiated with about 5000W/m^2^, and radiate 2500W/m^2^ from each surface, minus the power it radiates as communication energy. The black body temperature of the ring would be 460K. From the earth, the sky be the point source of a dimmed sun, the outer shell at 67K, and 75% of the ring band, 1.76 radians (101 angular degrees) wide and 0.01 radians (0.5 degrees) tall in the middle (42E6 km away) and 0.004 radians (0.22 degrees) tall at the limbs (104E6 km away). The porous band would occupy about 0.011 steradians of the sky. The outer shell would add 1.15 W/m^2^ to the earth's incoming heat, and the band would add 2.2 W/m^2^, (2500W/m^2^ * 0.011 / 4pi ). To keep the Earth at the same temperature as today, we can lower the solar light input by 3.4 W/m^2^ out of 1366 W/m^2^ . |
Server Sky to Dyson Shell
The following is extremely speculative. The intent is not to outline What Must Happen, but to estimate upper bounds for Server Sky.
Gerard K. O'Neill once asked whether planetary surfaces were the best place for industrial civilizations; his answer was "no", put them in Earth-Moon Lagrange orbits . Robert Forward said "ask the next question", which could be "are inner solar systems the best place for Type II Kardeshev civilizations (harnessing the entire output of a star)?" The answer to that question is probably "no", as well.
Freeman Dyson once proposed that advanced civilizations could be identified by their infrared emissions. Eventually, they would capture all the light from their stars, and turn the power into heat. The specific mechanism was unspecified, but would resemble a material shell surrounding the star. NOT a solid sphere; Dyson proposed (see reference below) something more like a layer of myriads of orbiting objects.
Light is very low entropy energy. Black body heat is high entropy energy. A very high efficiency computer would capture optical photons from the sun, between 1eV and 4eV, use the energy for processing, and emit 2.7K black body infrared photons, a spectrum centering around 240 microelectron volts. However, such a shell would be light-years across; anything closer will be warmer.
The temperature of the shell, assuming 1366 W/m2 at 1 AU and an emissivity of one, is (1366/5.6704e-8)1/4 R1/2 or 393.97/&sqrt;Rau Kelvin.
R(au) |
T (K) |
|
1 |
394.0 |
|
2 |
278.6 |
|
5 |
176.2 |
|
10 |
124.6 |
|
20 |
88.1 |
|
50 |
55.7 |
|
100 |
39.4 |
|
200 |
27.9 |
Hydrogen sphere freezes |
500 |
17.6 |
|
1000 |
12.4 |
0.0158 light years |
The lightest possible thin satellite will have zero orbital velocity, and hover in a balance between light pressure and solar gravity. This balance is the same throughout the solar system - both the light pressure and the gravity drop off as the inverse square. At the orbital radius of the Earth, the solar illumination is 1366 watts per meter squared, producing light pressure of P/c = 4.6 microPascal . The solar gravitational acceleration is 5.93 mm/s2. So the mass per unit area is the pressure divided by the acceleration, or about 0.75 grams per meter squared.
For a complete shell, though, this will be modified by infrared heat emission and absorption. The shell has a temperature, at equilibrium when the outbound infrared flux equals the inbound light flux. Assuming inner and outer black body surfaces with an emissivity of 1, then heat flux emitted inbound, and the flux absorbed from the rest of the inside of the shell, equals the emitted heat flux (and the light flux). The internal emitted heat, the internal absorbed heat, and the internal light flux combine to generate 3 times as much light pressure as the sunlight alone. The outward emitted heat flux light pressure works against that pressure. The sum of 3 outwards pressures and one inwards pressure is twice the outward pressure. The mass density must be doubled to compensate, for a mass per unit area of 1.5 grams per meter squared, or 1500 kilograms per kilometer squared.
If the material is carbon, with a density of 3 grams per centimeter squared, that corresponds to a thickness of 500 nanometers. Given that a graphene sheet is a fraction of a nanometer thick, that is a fairly thick structure and can contain much complexity.
The size of the shell is limited by the available material. One possible source is Neptune, with a mass of 1.02E26 kilograms. The atmosphere is approximately 1.5% methane by volume, and approximately 7% carbon by weight. If this is true of the whole planet, then Neptune contains about 7E27 grams of carbon (big if!!!).
A shell with a radius of 50 astronomical units, or 7.5E12 meters, has an area of 7E26 square meters. At 1.5 grams per square meter, that is 1E27 grams of carbon, about 15% of Neptune's carbon. Note that if Neptune has less methane, and a water or rock core, that core material can be used as "ballast" on a thinsat, with correspondingly less active carbon. One way or another, the shell of thinsats could be built with about 1% of the mass of Neptune.
Neptune has an escape velocity of 23500 meters per second, so the energy required to lift a kilogram out of its gravity well is 280 megajoules. A kilogram of hovering satellite, pre shell, in a 2.7K uniform background, covers 1300 square meters, and absorbs 2KW - if that was somehow all turned into launch energy, then the hovering satellites could lift their own mass in 140K seconds, or about 40 hours. Assuming 10% efficiency, that changes to 400 hours, the exponential growth time. Growing from a starting mass of 1E6 grams to a mass of 1E27 grams requires about 50x40 hours, about 3 months. Obviously, rates will be limited by other issues besides the power limits of partly disassembling Neptune, such as manufacturing and transit times.
A shell at 50AU will have a light flux of 0.55 watts per meter squared. The black body temperature is 56K. This will replace the current night sky temperature of the earth, which now emits 341.5 watts per meter squared, and will emit 342.05 watts per meter squared after envelopment. This will result in "global warming" of about 0.13C. Which could easily be mitigated with a few terawatts of refrigeration, or day/night albedo modification, or separating CO2 and launching some of the carbon.
The shell is outside the orbit of Pluto. At that distance, parallax is fairly small, and a tiny fraction of retro-reflectors, pointed at earth, could be used to simulate some fake stars. Since some birds navigate by the stars, this preserves their environment. It would sure upset the astronomers, but by that time, the will have moved their telescopes beyond Pluto, anyway.
Again, this is all very wild and speculative, but it does estimate the "limits to growth" for server-sky technology over the coming centuries. If we assume a 500 year buildout to 380 trillion terawatts, and start with the current 15 terawatts for human industrial consumption, then the compounded real growth rate is 6.4% per year.
Or, starting with a billion dollar investment, and pricing generation and computing at a dollar per watt, then the compounded investment growth rate will be 8.4% over 500 years. Over such large spans of time, it is very difficult to compare value, but however it is computed, this can support the growth of civilization and investment for a very long time.
And what would we do with such a shell? Perhaps some form of DigitalImmortality.
Hydrogen Ballast Shell
An even colder shell could provide more computation per watt of sunlight, because the energy per bit could be reduced. Reducing the temperature by 4x (to 14K) would require 256x the area and 16x the distance, and there is not enough carbon in the solar system to do that without some form of ballast. However, 14K is cold enough to freeze hydrogen, and that could become the ballast, perhaps frozen into lenses on the front surface of the thinsats, with the carbon concentrated at the foci. The resulting computation would be slower and more widely dispersed, but more powerful overall. Such a system could move further and further out, consuming more and more of the hydrogen in the solar system, and the shells would become increasingly hard to detect against the 2.7K cosmic background.
Perhaps that is what some "dark matter" actually is. Brownlee and Ward's "Rare Earth" teaches us that advanced civilizations are probably incredibly rare, perhaps one per several galaxies. However, in a few billion years, a few advanced civilizations may engulf most of the stars in large clusters of nearby galaxies, leading to large voids in the sky and anomalously high mass to light ratios. These large spheres would occult stars (though not galaxies) behind them; a very high resolution space telescope capable of observing individual stars billions of light years away, millions of stars, might detect a few these decade-long occultations.
Visibility of a Dyson Shell
A hypothetical giant telescope mirror 100 meters across and 100 light years away might intercept 1.1E-32 of the Sun's output, about 4 microwatts. At that distance, the Sun would be magnitude 7.6, not quite visible to an unaided human eye. If intelligent life is rare and widely spaced, then chances are nobody would notice if we captured all the light.
On the other hand, consider a 50AU diameter Dyson shell surrounding our sun, with an average black body temperature of 56K and a peak infrared wavelength of 50 microns by Wein's Law. That would be quite visible (and anomalous!) to a very distant astronomer with a very large, orbiting infrared telescope. An orbiting 1000 meter collector would see a round object (rather than a diffuse cloud) at 10,000 light years; such a collector ( including a triple layer reflector and outside a similar Dyson shell ) might weigh a few tons, an infinitesimal fraction of total shell weight. Large, sharp-edged infrared spheres may prove to be the most reliable sign of well behaved shell civilizations elsewhere. Once such civilizations are discovered, narrow beam optical wavelength interstellar communication becomes possible.
Solar heating over time
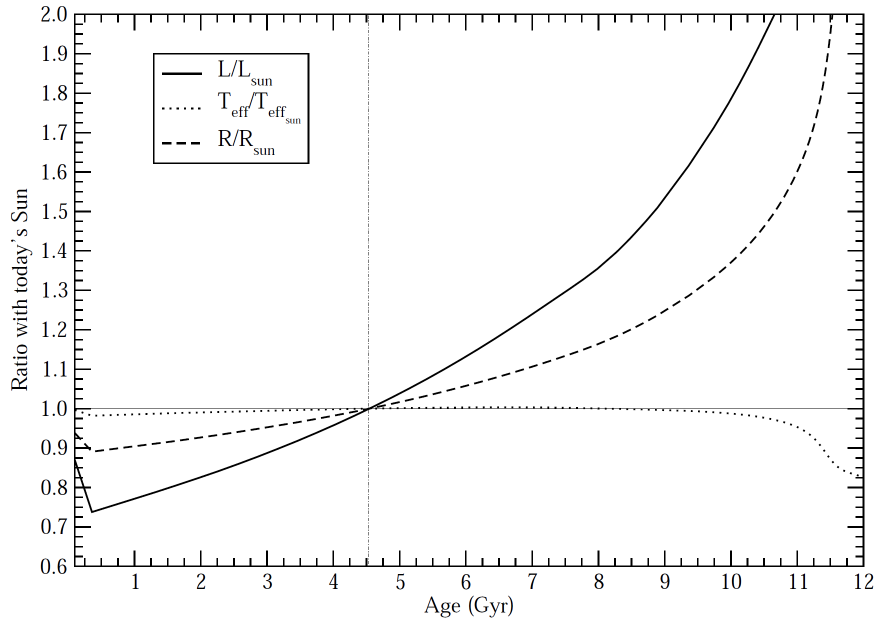
The balance of light to mass holds the thinsat shell in place. As the sun ages, irradiation increases, by a factor of two over the next 10 billion years. This can be accommodated by doubling the mass density of the thinsats, perhaps combining them and letting some light (and heat) escape through gaps. Both illumination and gravity drop off as the inverse square, so the need for extra mass is the same throughout the solar system. The black body radiation will double in 10 billion years, so the temperature of a doubled mass, non-porous 50AU shell might increase from 56K to 67K. If it is porous, there will be less self-irradiation and the temperature will drop somewhat.
The earth will not do so well. Without compensation, the temperature of the earth would increase by about 50K, which would kill all plants, fill the atmosphere with many atmospheres of CO2 , and evolve towards the conditions of current-day Venus, a 460C hellhole receiving a little less than twice Earth's irradiation.
Angel Shield at L1, 0.99 AU
A possible solution would be a variation of Roger Angel's Space Sunshade. Dr. Angel proposes a constellation of transparent lens thinsats at the Earth-Sun Lagrange 1 point (1.5e6 kilometers sunwards from the earth, about 1% of the sun's distance), scattering light away from the Earth. Scattering as much as half of sunlight over cosmic-scale time may prove difficult; the lenses would need frequent repositioning and refurbishment. L1 is unstable, and some of the strays could eventually fall into orbits behind the earth, reflecting light into the night sky and adding to the heat. These are probably solvable problems.
Instead of an Angel Sunshade, let's consider "floating thinsats" instead, because we can also use it as a radio repeater near the inner solar system, suitable for relaying communications between Earth and the outer shell.
Orbiting/Hovering disk shield at 0.95 AU
An object at 0.95 AU is 5 times as far away as Lagrange 1; it will not feel much perturbation from the Earth ( 7e-6 m/s2 at conjunction) or Venus ( 2.8e-7 m/s2 at conjunction ) or Jupiter (3.1e-7 m/s2 at conjunction).
At 0.95 AU, and 5.5 billion years from now, with an expanded solar sphere about 2E6 km in diameter ( 1.4*1.4E6 km ), a shield 5% of the way towards the Sun ( 7.5e6 km sunwards ) must be at least 100,000 kilometers across; assume 200,000 km with a safety factor of 2. A disk of thinsats tracking the earth will feel strong tidal forces. The gravity deflecting the Earth into its circular orbit is ~\omega^2 R ~ = ~ ( { { 2 \pi } \over T } )^2 R ~ = ~ 5.93 mm/s2 . At 0.95 AU, a disk shadowing the earth will see 16% of that, about 0.95 mm/s2 ( 9.5e-4 m/s2 ) pulling it towards the sun. If the disk is partly reflective, producing about 1e-5 Pa of light pressure (the sun is brighter) then a disk density of about (1e-5/1e-3) or 0.01 kg/m2 will balance it. The area of the disk is 3.1e16 m2 so the mass (at 50% opacity) is around 1.5e14 kg. That is around 5e10 cubic meters of earth-density rock, about 50 cubic kilometers, the material in a medium-sized asteroid. Such an asteroid could be robotically manufactured into thinsats, which could sent down to a gravity-assist slingshot around the earth, then into the 0.95 AU orbit.
Assuming both reflectivity and emissivity of 50% on both front and back (after being scoured by micrometeorites), the black body radiation power on both sides is equivalent to 700W/m2 on each side. Assuming isotropic radiation on both sides, the filled area of 1.5e16 m2 will emit around 1e19 watts, at a distance of 7.5 million kilometers. If the heat is radiated isotropically, the heat flux on the earth will be 1e19W /( 2 π 7.5e92 m2) or 30 mW/m2 - negligible compared to the 1366W/m2 of sunlight we continue to let through.
Static hovering ring shield at 0.95 AU
The shield could be a ring of static, hovering thinsats, in the full gravity of the sun, about 6.57 mm/s2, or about 6.9 times the acceleration of the orbiting disk. That means that for the same light pressure, the ring is 6.9x less dense, 1.45e-3 kg/m2. But the ring must extend all the way around the Sun, 8.5E11 meters, and is 200,000 km across, for a total area of 1.7E20 m2 and a mass of 1.2e17 kg, about 80 times the mass of the orbiting disk, and about 1% of the mass of the asteroids Vesta or Pallas. While this seems more difficult than the orbiting disk, the total energy intercepted would be 4.6E23 watts, about half a trillion terawatts, which could be used for many interesting tasks; communication, computation, propulsion power.
Assuming the same emissivity as before, 700W/m2, the ring will emit 7e10W per meter of length. Divided by a half cylinder distance of 7.5e9 meters, and a half circumference of 2.35e9 meters, that is 3 watts per square meter at the distance of the earth. Much larger than the previous case, but still tiny compared to the 1366W/m2 sunlight we are letting though. The result is about the same for the static Venus ring discussed below.
Static ring replacing Venus at 0.723 AU
Imagine a ring of thinsats around the orbit of Venus; static, not orbiting. The ring is very thin, and wide enough to block the image of the Sun from the Earth, about 1 million kilometers wide, at a distance of 108 million kilometers. The ring is about 50% porous, and the thinsats have a density of 1.5 grams per square meter, smaller than the outer shell because the ring is too porous and incomplete to self-irradiate and add extra light pressure.
The total mass of this porous ring is 8E17 kg ( 0.5 * 1.5E3 kg/km2 * 108E6 km * 1e6 km ), a tiny fraction of Venus's 4.87E24 kg mass, most of which would be sent out to add (slightly) to the outer shell. The ring would be irradiated with about 5000W/m2, and radiate 2500W/m2 from each surface, minus the power it radiates as communication energy. The black body temperature of the ring would be 460K. From the earth, the sky be the point source of a dimmed sun, the outer shell at 67K, and 75% of the ring band, 1.76 radians (101 angular degrees) wide and 0.01 radians (0.5 degrees) tall in the middle (42E6 km away) and 0.004 radians (0.22 degrees) tall at the limbs (104E6 km away). The porous band would occupy about 0.011 steradians of the sky. The outer shell would add 1.15 W/m2 to the earth's incoming heat, and the band would add 2.2 W/m2, (2500W/m2 * 0.011 / 4pi ). To keep the Earth at the same temperature as today, we can lower the solar light input by 3.4 W/m2 out of 1366 W/m2 .
If a large fraction of the intercepted power (3.4 trillion terawatts) could be turned into beamed energy pointed at a small area of the Sun, it could double the black body temperature of 3 billion square kilometers of the surface, about the 15% of the size of a sunspot. That might be useful for something. Perhaps there is some way to use tuned monochromatic light to make the Sun eject a bit of useful helium, or heavier elements, from the photosphere. This won't slow down the helium-ash expansion of the sun, but it might be a source of carbon for construction. Figuring out how, or even if, is way beyond my competence.
These disks and rings are far more extensive projects than the Angel Sunshield. They can provide exawatts of power for Earth-to-shell broadcast, as a component of a Kardeshev type II civilization, with about a million times the power and antenna surface of the Earth. Computing would be 10x less efficient than the colder outer shell, and the radiation damage 5000 times higher, so this would not be a good place for computing and information storage.
Recap
The preceding is wild speculation, of course. Far future extensions of Server Sky technology, built over thousands of years, can support computation in space for billions of years, even while the Sun warms towards its red giant finish. How the technology will play out will be determined by those who build it, or don't, correctly or wastefully.
References
Ignasi Ribas (2009) "The Sun and stars as the primary energy input in planetary atmospheres", arXiv:0911.4872v1 [astro-ph.EP] 25 Nov 2009
Freemann J. Dyson (1960). "Search for Artificial Stellar Sources of Infra-Red Radiation". Science 131 (3414): 1667–1668. doi:10.1126/science.131.3414.1667. PMID 17780673.
