Rws - Server Sky to Dyson Shell
The following is extremely speculative. The intent is not to outline What Must Happen, but to estimate upper bounds for Server Sky.
Dyson shell objects need not be in orbit. If they are stationary and supported by light pressure, they can be very light weight and thin. They can be even thinner if their backside infrared emissions, pointed away from the sun, partly balance the light pressure from the Sun on the front side.
At 50 AU distance (7.48e12 meters), the gravitational force from the sun ( μ = 1.327e20 m3/s2 ) is 2.37e-6 m/s2. The sunlight power is 0.547 W/m2. This produces a light pressure of 1.825e-9 Pascals. These balance at 0.77 g/m2.
If this light impinged on an absorbent thinsat with infrared filtering emitting isotropic infrared away from the sun, the light pressure would be around 9e-10 Pa. The light pressure and the gravitational force would balance with a sheet of material massing 0.38 g/m2 - about 400 nanometers of solid ice, for example. The actual structure will probably be gossamer, with voids and internal structures composed of many elements.
Presuming the infrared emission is Lambertian, if it is on the outer side only it will compensate for 2/3 of the light pressure, and the shell would weigh 0.26 g/m2. If it emissive is on both sides, the inner infrared is both emitted and absorbed, and the net light pressure increases to 5/3 of the optical light pressure, supporting 1.28 g/m2. In the latter case, the infrared bath would raise the earth's black body heat flux by 0.23% and temperature by 0.15 C. It would raise the temperature of Uranus by 5 to 7 Kelvin, and Neptune by 11 Kelvin. Hopefully, the system will be lighter weight and cooler.
The sun produces 1.3e36 solar wind particles per second. At the 50AU outer shell, with an area of 7e26m2, this would be 2e9 particles /m2-s or 0.06 particles /nm2-year . This seems like a lot, although the photon energy flux is 3.4e18 eV per second, compared to 1e15 eV/second of particles.
Surrounding and imbedded in this structural ice could be surfaces and structures for capturing the light from the sun and efficiently converting it to computation and information storage - probably using carbon, nitrogen, and other elements. Slight variations in light pressure provide active control of radial and tangential position, compensating for errors, shading, and the tidal perturbations of Jupiter ( μ=1.27e17 m3/s2, R=5.20 AU, a=±2.4e-10 m/s2 ), Saturn ( μ=3.79e16 m3/s2, R=9.54 AU, a=±1.3e-10 m/s2 ), Uranus ( μ=5.79e15 m3/s2, R=19.2 AU, a=±0.4e-10 m/s2 ), and Neptune ( μ=6.84e15 m3/s2, R=30.1 AU, a=±0.7e-10 m/s2 ) will require small, very slow control changes. Presumably, most of the errors will be due to distance measurement.
Gerard K. O'Neill once asked whether planetary surfaces were the best place for industrial civilizations; his answer was "no", put them in Earth-Moon Lagrange orbits . Robert Forward said "ask the next question", which could be "are inner solar systems the best place for Type II Kardeshev civilizations (harnessing the entire output of a star)?" The answer to that question is probably "no", as well.
Freeman Dyson once proposed that advanced civilizations could be identified by their infrared emissions. Eventually, they would capture all the light from their stars, and turn the power into heat. The specific mechanism was unspecified, but would resemble a material shell surrounding the star. NOT a solid sphere; Dyson proposed (see reference below) something more like a layer of myriads of orbiting objects.
Light is very low entropy energy. Black body heat is high entropy energy. A very high efficiency computer would capture optical photons from the sun, between 0.5 eV and 4.5 eV, use the energy for processing, and emit 2.7K black body infrared photons, a spectrum centering around 240 microelectron volts. However, such a shell would be light-years across; anything closer will be warmer.
The lightest possible thin satellite will have zero orbital velocity, and hover in a balance between light pressure and solar gravity. This balance is the same throughout the solar system - both the light pressure and the gravity drop off as the inverse square. At the orbital radius of the Earth, the solar illumination is 1366 watts per meter squared, producing light pressure of P/c = 4.6 microPascal . Infrared filtering and isotropic backside heat emissions cut the light pressure in half. The solar gravitational acceleration at 1 AU is 5.93 mm/s2. So the mass per unit area is the pressure divided by the acceleration, or about 0.39 grams per meter squared.
If the material is carbon, with a density of 3 grams per centimeter squared, that corresponds to a thickness of 130 nanometers. Given that a graphene sheet is a fraction of a nanometer thick, that is a fairly thick structure and can contain much complexity. Ice is a more interesting material, stable at 60 K over billions of years, though the shell will presumably need carbon and nitrogen and other elements to construct complex nano-scale systems. Ice has a glass transition temperature of 120 to 140 Kelvin.
The Stefan-Boltzmann constant is \sigma = 5.67e-8 W/m2K4 . An astronomical unit is 1.496e11 meters, and the area of a spherical shell is 2.81e23 m2 × R(au)2.
The temperature of the shell, assuming 1366 W/m2 at 1 AU and an IR emissivity of 1.0, is (1366/5.6704e-8)1/4 R-1/2 or 394/√Rau Kelvin. The Wien peak blackbody emission wavelength λ is 2898 μm-K / T, the Wien peak frequency is 58.79 GHz/K, and the Wien peak energy is 0.2431 meV/k . The mass (in earth masses, ME, 5.972e24 kg), assuming 400 milligrams per square meter, is 1.9e-5 Rau2:
Rau |
T (K) |
ME |
|
Rau |
Vesc |
T (K) |
ME |
λ |
GHz |
meV |
1 |
394.0 |
1.9e-5 |
50 |
5965 m/s |
55.7 |
4.7e-2 |
52μm |
3300 |
13 |
this example |
2 |
278.6 |
7.5e-5 |
100 |
4218 m/s |
39.4 |
0.19 |
74μm |
2300 |
10 |
heliopause |
5 |
176.2 |
4.7e-4 |
500 |
1886 m/s |
17.6 |
4.7 |
160μm |
1000 |
4.3 |
Hydrogen sphere freezes |
10 |
124.6 |
1.9e-3 |
1000 |
1334 m/s |
12.4 |
19 |
230μm |
730 |
3.0 |
0.0158 light years |
20 |
88.1 |
7.5e-3 |
4800 |
609 m/s |
5.7 |
446 |
510μm |
340 |
1.4 |
Assume a 50 AU shell. That is a tradeoff between maximizing computational efficiency and sensor sensitivity (colder is better), speed of light communication (closer is better), and the shielding effects of the solar magnetic field (which yields to the galactic magnetic field at the heliopause). At 0.4 g/m2, the total 50 AU shell mass is about 2.8e23 kilograms, and the area is 7e26 m2. That is 4.7% of the Earth's mass.
Kuiper belt objects may be sufficient to construct the shell, the total mass ranging from 4% to 10% of the Earth's mass ME. A larger source of materials is Neptune, with a mass of 1.02E26 kilograms, or 17 ME. The atmosphere is approximately 1.5% methane by volume, and approximately 7% carbon by weight. If this is true of the whole planet, then Neptune contains about 7e24 kilograms of carbon (big if!!!). Over billions of years, as the sun heats up over millions of years, its luminosity will increase, requiring more mass per square meter, and a more distant, large-area shell to maintain a low temperature, so Neptune may be partially cannibalized, as well as some of the distant Oort cloud.
Neptune has an escape velocity of 23500 meters per second, so the energy required to lift a kilogram out of its gravity well is 280 megajoules. A kilogram of hovering satellite at Neptune orbital radius (30 AU) covers 2500 square meters, and absorbs 3.8 KW - if that was turned into launch energy with 1% efficiency, then the hovering satellites could lift their own mass in 5.3M seconds, or about 1500 hours. Growing exponentially from a starting mass of 1E6 grams to a mass of 1E27 grams requires about 50x1500 hours, about 9 earth years. Rates will likely be limited by other issues besides the power limits of partly disassembling Neptune, such as manufacturing and transit times, and most importantly, demand.
A shell at 50AU will have a light flux of 0.55 watts per meter squared. The black body temperature is 56K. This will replace the current night sky temperature of the earth, which now emits 341.5 watts per meter squared, and will emit 342.05 W/m2 after envelopment. This will result in "global warming" of about 0.13C. Which could easily be mitigated with a few terawatts of refrigeration, or day/night albedo modification, or separating CO2 and launching some of the carbon.
The shell is outside the orbit of Pluto. At that distance, parallax is fairly small, and a tiny fraction of retro-reflectors, pointed at earth, could be used to simulate some fake stars. Since some birds navigate by the stars, this preserves their environment. It would sure upset the astronomers, but by that time, they will have moved their telescopes into the shell. If 1% of the shell is used for astronomy, it can collect 2.5e23 times the energy of the James Webb Space Telescope.
Again, this is all very wild and speculative, but it does estimate the "limits to growth" for server-sky technology over the coming centuries. If we assume a 500 year buildout to 380 trillion terawatts, and start with the current 15 terawatts for human industrial consumption, then the compounded real growth rate is 6.4% per year.
Or, starting with a billion dollar investment, and pricing generation and computing at a dollar per watt, then the compounded investment growth rate will be 8.4% over 500 years. Over such large spans of time, it is very difficult to compare value, but however it is computed, this can support the growth of civilization and investment for a very long time.
And what would we do with such a shell? Perhaps some form of DigitalImmortality.
Hydrogen Ballast Shell
An even colder shell could provide more computation per watt of sunlight, because the energy per bit could be reduced. Reducing the temperature by 4x (to 14K) would require 256x the area and 16x the distance, and there is not enough carbon in the solar system to do that without some form of ballast. However, 14K is cold enough to freeze hydrogen, and that could become the ballast, perhaps frozen into lenses on the front surface of the thinsats, with the carbon concentrated at the foci. The resulting computation would be slower and more widely dispersed, but more powerful overall. Such a system could move further and further out, consuming more and more of the hydrogen in the solar system, and the shells would become increasingly hard to detect against the 2.7K cosmic background.
Perhaps that is what some "dark matter" actually is. Brownlee and Ward's "Rare Earth" teaches us that advanced civilizations are probably incredibly rare, perhaps one per several galaxies. However, in a few billion years, a few advanced civilizations may engulf most of the stars in large clusters of nearby galaxies, leading to large voids in the sky and anomalously high mass to light ratios. These large spheres would occult stars (though not galaxies) behind them; a very high resolution space telescope capable of observing individual stars billions of light years away, millions of stars, might detect a few these decade-long occultations.
Visibility of a Dyson Shell from Distant Stars
A hypothetical giant telescope mirror 100 meters across and 100 light years away might intercept 1.1E-32 of the Sun's output, about 4 microwatts. At that distance, the Sun would be magnitude 7.6, not quite visible to an unaided human eye. If intelligent life is rare and widely spaced, then chances are nobody would notice if we captured all the light.
On the other hand, consider a 50 AU diameter Dyson shell surrounding our sun, with an average black body temperature of 56K and a peak infrared wavelength of 50 microns by Wein's Law. That would be quite visible (and anomalous!) to a very distant astronomer with a very large, orbiting infrared telescope. An orbiting 1000 meter collector would see a round object (rather than a diffuse cloud) at 10,000 light years; such a collector ( including a triple layer reflector and outside a similar Dyson shell ) might weigh a few tons, an infinitesimal fraction of total shell weight. Large, sharp-edged infrared spheres may prove to be the most reliable sign of well behaved shell civilizations elsewhere.
Once such civilizations are discovered, narrow beam optical wavelength interstellar communication becomes possible.
Visibility from the Inside - the Dark Gray Sky
Unless the shell has an albedo of zero, it will reflect some light back towards the inner solar system. Flat solar-cell-like surfaces will have an index of refraction, and inevitably some of the light will reflect. If a 50 AU shell has an albedo of 0.1, it will be illuminated with 550 mW per square meter, and reflect 55 mW per square meter. The shell will be 50 AU away, attenuated by inverse square, but it will also be 15,700 square AU in size, a lot of emitting surface. This will be the equivalent of 55 mW/m2 illumination of the night sky of earth (by symmetry), about 38 lux, approximately 80 times the full moon.
Presumably, the shell will grow to absorb all the light. The risk is to sensitive earth-life, not to the builders of the shell. The technological trick is to make lighting up the earth's night sky unprofitable, not merely immoral, because intelligences can rationalize anything. Some of "ecological activism" is rationalized envy, for example, though they would make much more progress if they were clever enough to make sustainability broadly profitable and painless, rather than political.
A solar cell will absorb more if light hits it at the Brewster angle, so the cells (however they are made) should have a sawtooth surface. Any reflected light will scatter sideways. If the sawtooth is assymetric, the light could bounce three or four times before any leaks back towards the inside. And if we do it right, that reflected light will not reflect directly back towards the sun, but a couple of degrees to either side, lighting up the asteroids and outer planets a little, but not the earth.
Eventually, the reflected infrared and light will heat up the outer planets; material is too gravitationally bound to the planets themselves, but it might eventually evaporate the most volatile materials in the rings of Uranus and Neptune. Those planets and their rings will probably be the raw materials to build the shell, anyway.
Solar heating over time
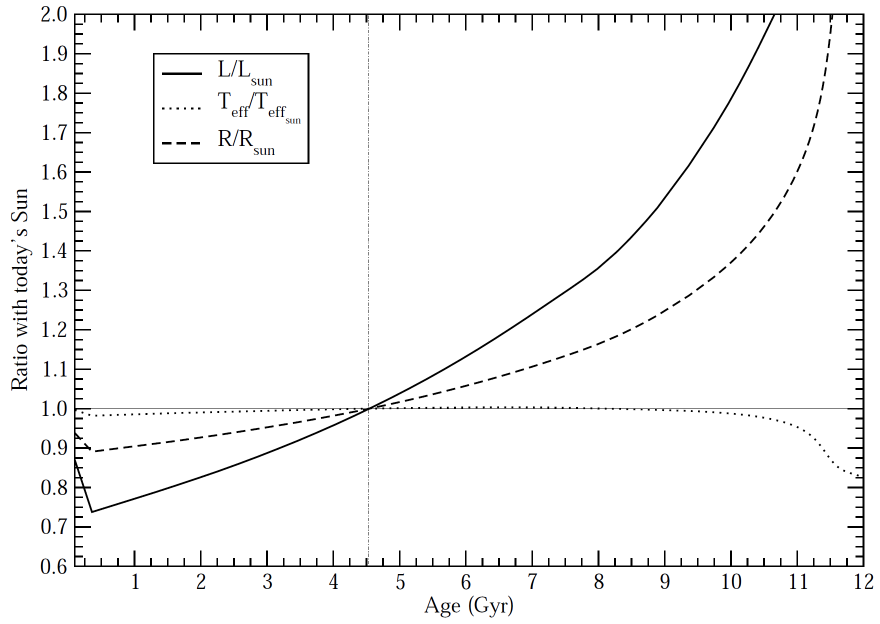
The balance of light to mass holds the thinsat shell in place. As the sun ages, irradiation increases, by a factor of two over the next 6 billion years. This can be accommodated by doubling the mass density of the thinsats, perhaps combining them and letting some light (and heat) escape through gaps. Both illumination and gravity drop off as the inverse square, so the need for extra mass is the same throughout the solar system. The black body radiation will double in 10 billion years, so the temperature of a doubled mass, non-porous 50AU shell might increase from 56K to 67K. If it is porous, there will be less self-irradiation and the temperature will drop somewhat.
The earth will not do so well. Without compensation, the temperature of the earth would increase by about 50K, which would kill all plants, fill the atmosphere with many atmospheres of CO2 , and evolve towards the conditions of current-day Venus, a 460C hellhole receiving a little less than twice Earth's irradiation.
Angel Shield at L1, 0.99 AU
A possible solution would be a variation of Roger Angel's Space Sunshade. Dr. Angel proposes a constellation of transparent lens thinsats at the Earth-Sun Lagrange 1 point (1.5e6 kilometers sunwards from the earth, about 1% of the sun's distance), scattering light away from the Earth. Scattering as much as half of sunlight over cosmic-scale time may prove difficult; the lenses would need frequent repositioning and refurbishment. L1 is unstable, and some of the strays could eventually fall into orbits behind the earth, reflecting light into the night sky and adding to the heat. These are probably solvable problems.
Instead of an Angel Sunshade, let's consider "floating thinsats" instead, because we can also use it as a radio repeater near the inner solar system, suitable for relaying communications between Earth and the outer shell.
Orbiting/Hovering disk shield at 0.95 AU
An object at 0.95 AU is 5 times as far away as Lagrange 1; it will not feel much perturbation from the Earth ( 7e-6 m/s2 at conjunction, viewed from the Sun) or Venus ( 2.8e-7 m/s2 at conjunction ) or Jupiter (3.1e-7 m/s2 at conjunction).
At 0.95 AU, and 5.5 billion years from now, with an expanded solar sphere about 2E6 km in diameter ( 1.4*1.4E6 km ), a shield 5% of the way towards the Sun ( 7.5e6 km sunwards ) must be at least 100,000 kilometers across; assume 200,000 km with a safety factor of 2. A disk of thinsats tracking the earth will feel strong tidal forces. The gravity deflecting the Earth into its circular orbit is ~\omega^2 R ~ = ~ ( { { 2 \pi } \over T } )^2 R ~ = ~ 5.93 mm/s2 . At 0.95 AU, a disk shadowing the earth will see 16% of that, about 0.95 mm/s2 ( 9.5e-4 m/s2 ) pulling it towards the sun. If the disk is partly reflective, producing about 1e-5 Pa of light pressure (the sun is brighter) then a disk density of about (1e-5/1e-3) or 0.01 kg/m2 will balance it. The area of the disk is 3.1e16 m2 so the mass (at 50% opacity) is around 1.5e14 kg. That is around 5e10 cubic meters of earth-density rock, about 50 cubic kilometers, the material in a medium-sized asteroid. Such an asteroid could be robotically manufactured into thinsats, which could sent down to a gravity-assist slingshot around the earth, then into the 0.95 AU orbit.
Assuming both reflectivity and emissivity of 50% on both front and back (after being scoured by micrometeorites), the black body radiation power on both sides is equivalent to 700W/m2 on each side. Assuming isotropic radiation on both sides, the filled area of 1.5e16 m2 will emit around 1e19 watts, at a distance of 7.5 million kilometers. If the heat is radiated isotropically, the heat flux on the earth will be 1e19W /( 2 π 7.5e92 m2) or 30 mW/m2 - negligible compared to the 1366W/m2 of sunlight we continue to let through.
Static hovering ring shield at 0.95 AU
The shield could be a ring of static, hovering thinsats, in the full gravity of the sun, about 6.57 mm/s2, or about 6.9 times the acceleration of the orbiting disk. That means that for the same light pressure, the ring is 6.9x less dense, 1.45e-3 kg/m2. But the ring must extend all the way around the Sun, 8.5E11 meters, and is 200,000 km across, for a total area of 1.7E20 m2 and a mass of 1.2e17 kg, about 80 times the mass of the orbiting disk, and about 1% of the mass of the asteroids Vesta or Pallas. While this seems more difficult than the orbiting disk, the total energy intercepted would be 4.6E23 watts, about half a trillion terawatts, which could be used for many interesting tasks; communication, computation, propulsion power.
Assuming the same emissivity as before, 700W/m2, the ring will emit 7e10W per meter of length. Divided by a half cylinder distance of 7.5e9 meters, and a half circumference of 2.35e9 meters, that is 3 watts per square meter at the distance of the earth. Much larger than the previous case, but still tiny compared to the 1366W/m2 sunlight we are letting though. The result is about the same for the static Venus ring discussed below.
Static ring replacing Venus at 0.723 AU
Imagine a ring of thinsats around the orbit of Venus; static, not orbiting. The ring is very thin, and wide enough to block the image of the Sun from the Earth, about 1 million kilometers wide, at a distance of 108 million kilometers. The ring is about 50% porous, and the thinsats have a density of 1.5 grams per square meter, smaller than the outer shell because the ring is too porous and incomplete to self-irradiate and add extra light pressure.
The total mass of this porous ring is 8E17 kg ( 0.5 * 1.5E3 kg/km2 * 108E6 km * 1e6 km ), a tiny fraction of Venus's 4.87E24 kg mass, most of which would be sent out to add (slightly) to the outer shell. The ring would be irradiated with about 5000W/m2, and radiate 2500W/m2 from each surface, minus the power it radiates as communication energy. The black body temperature of the ring would be 460K. From the earth, the sky be the point source of a dimmed sun, the outer shell at 67K, and 75% of the ring band, 1.76 radians (101 angular degrees) wide and 0.01 radians (0.5 degrees) tall in the middle (42E6 km away) and 0.004 radians (0.22 degrees) tall at the limbs (104E6 km away). The porous band would occupy about 0.011 steradians of the sky. The outer shell would add 1.15 W/m2 to the earth's incoming heat, and the band would add 2.2 W/m2, (2500W/m2 * 0.011 / 4pi ). To keep the Earth at the same temperature as today, we can lower the solar light input by 3.4 W/m2 out of 1366 W/m2 .
If a large fraction of the intercepted power (3.4 trillion terawatts) could be turned into beamed energy pointed at a small area of the Sun, it could double the black body temperature of 3 billion square kilometers of the surface, about the 15% of the size of a sunspot. That might be useful for something. Perhaps there is some way to use tuned monochromatic light to make the Sun eject a bit of useful helium, or heavier elements, from the photosphere. This won't slow down the helium-ash expansion of the sun, but it might be a source of carbon for construction. Figuring out how, or even if, is way beyond my competence.
These disks and rings are far more extensive projects than the Angel Sunshield. They can provide exawatts of power for Earth-to-shell broadcast, as a component of a Kardeshev type II civilization, with about a million times the power and antenna surface of the Earth. Computing would be 10x less efficient than the colder outer shell, and the radiation damage 5000 times higher, so this would not be a good place for computing and information storage.
Inner UV shell
Some propose a set of nested shells, with the heat radiation of an inner shell powering the next outer shell. This is analogous to multistage steam engines - and that is a terrible analogy, because low etendue, high energy, highly collimated light is far more useful and valuable than scattered low energy heat. Light is not steam.
However - a single inner shell, extremely thin, that stops all photons and particles with energy greater than 4.5 eV would protect the rest of the solar system, and the 50 AU shell, from damage. If we pass everything with energies below 4.5 eV and stop the rest in an inner shell, the inner shell could perform high speed computation with the power it stops, about 2% of the total flux. If it filters efficiently, and radiates on the back side isotropically, then about 1% of the light flux is making "lift" relative to the IR emitted from the back.
If we presume the inner shell is intercepting about 4 kW/m2 out of a total flux of 200 kW/m2, and has a backside emissivity of 0.8, it will heat to 545 K (272°C) and reradiate the power as mid-infrared, with a peak energy around 0.13 eV, and about 0.5% of the output flux ( 20W/m2) at energies above 0.5 eV, a hypothetical "minimum useful energy" for the outer shell, thus increasing outer shell power by 0.01% - not worth it as extra power, but worthwhile as protection. 200 kW/m2 happens at 0.083 AU, about 12.4 M km radius. The shell would have 1% of the net light pressure, and would weigh 15 mg/m2, or 15 kg/km2, total mass around 3e16 kg. If it is a ceramic with a density of 3, the shell will be 5 nanometers thick, and the total volume will be 10,000 km3.
If the energy is used to compute, it will be about 10 times less power efficient than the outer shell, and it will get 2% of the energy, so it might add 0.2% to the solar system's total computational capacity - probably less, though, because it will use a lot more energy for repair. It is probably worth considering running the shell at a lower temperature and higher radius:
Inner shell 2 - running at 300K. The shell is intercepting the same total power, but only 367 W/m2 out of a total flux of 18400 W/m2. Radius is 0.27 AU, 40 M km, just inside the perhelion of Mercury. The shell density is the same, but the shell has 10.8 times the area, and the total volume will be around 110,000 km3, equivalent to a solid 60 km diameter sphere of "undefine-ium". The compute power can be doubled because the bit energy is approximately half, perhaps 0.4% of total solar system compute capacity. 5 ppm of the radiated energy might be reusable, adding 0.1 ppm to the outer shell computation. This shell generates more computing, but its output heat is useless - it is a protective shield and a supplemental low-latency computer, not an energy source.
Recap
The preceding is wild speculation, of course. Far future extensions of Server Sky technology, built over thousands of years, can support computation in space for billions of years, even while the Sun warms towards its red giant finish. How the technology will play out will be determined by those who build it, or don't, correctly or wastefully.
References
Ignasi Ribas (2009) "The Sun and stars as the primary energy input in planetary atmospheres", arXiv:0911.4872v1 [astro-ph.EP] 25 Nov 2009
Freemann J. Dyson (1960). "Search for Artificial Stellar Sources of Infra-Red Radiation". Science 131 (3414): 1667–1668. doi:10.1126/science.131.3414.1667. PMID 17780673.