|
Size: 5969
Comment:
|
Size: 5668
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 17: | Line 17: |
| and lenses can reduce etendue of the whole beam, the quantity always increases. Black body radiation has maximum etendue; there's no way to focus it on a spot smaller than the emitting surface. If you could, that spot could be hotter than the source, violating the second law of thermodynamics. If someone thinks the 2nd law can be violated, suggest they eat shit ... and vomit gourmet food. Certainly the entropy of the words leaving their mouths is higher than the entropy of the words entering their ears. |
and lenses can reduce etendue of the whole beam, the quantity always increases. Black body radiation has maximum etendue; there's no way to focus it on a spot smaller than the emitting surface. If you could, that spot could be hotter than the source, violating the second law of thermodynamics. |
| Line 21: | Line 20: |
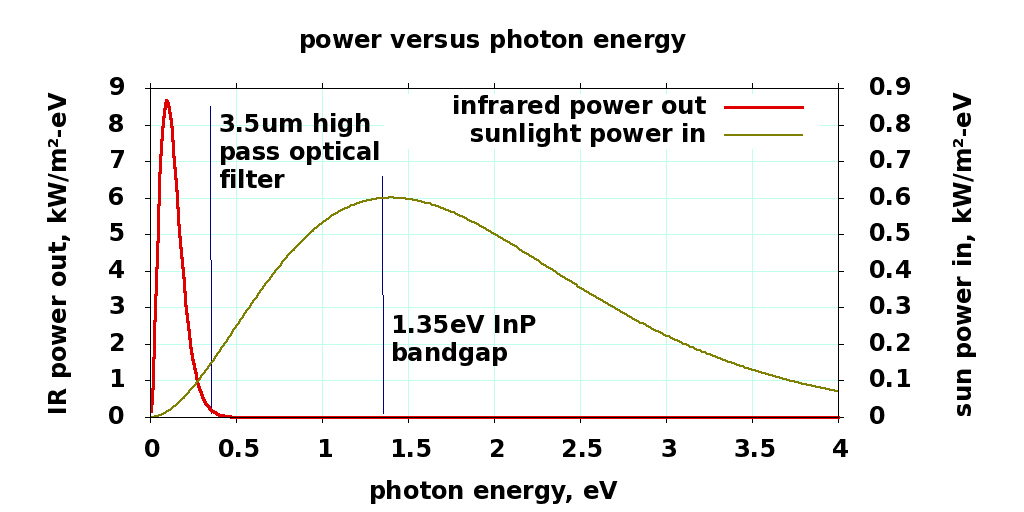
| || W/m²|| ||<|15>{{attachment:ir0.png||width=600}}|| || 1366.003||sun power || || 1346.857|| emitted power || || 1346.857|| absorbed power || || 19.146|| reflected power || || 8.915|| IR power emitted frontside || || 1337.942|| IR power emitted backside || || 499.131|| forward thrust power || || 573.745|| photovoltaic illumination power || || || || || || || || 392 K || Thinsat temperature || || 0.86995|| thrust/photovoltaic ratio || || 3.5 μm || filter wavelength || |
|| W/m² || ||<|15>{{attachment:ir0.png||width=640}}|| || 1366 || sun power || || 1347 || emitted power || || 1347 || absorbed power || || 19.1 || reflected power || || 8.9 || IR power emitted frontside || || 1338 || IR power emitted backside || || 499.1 || forward thrust power || || 573.7 || photovoltaic illumination || || || || || || || || 120°C || Thinsat temperature || || 0.87 || thrust/photovoltaic ratio || || 3.5 μm || filter wavelength || |
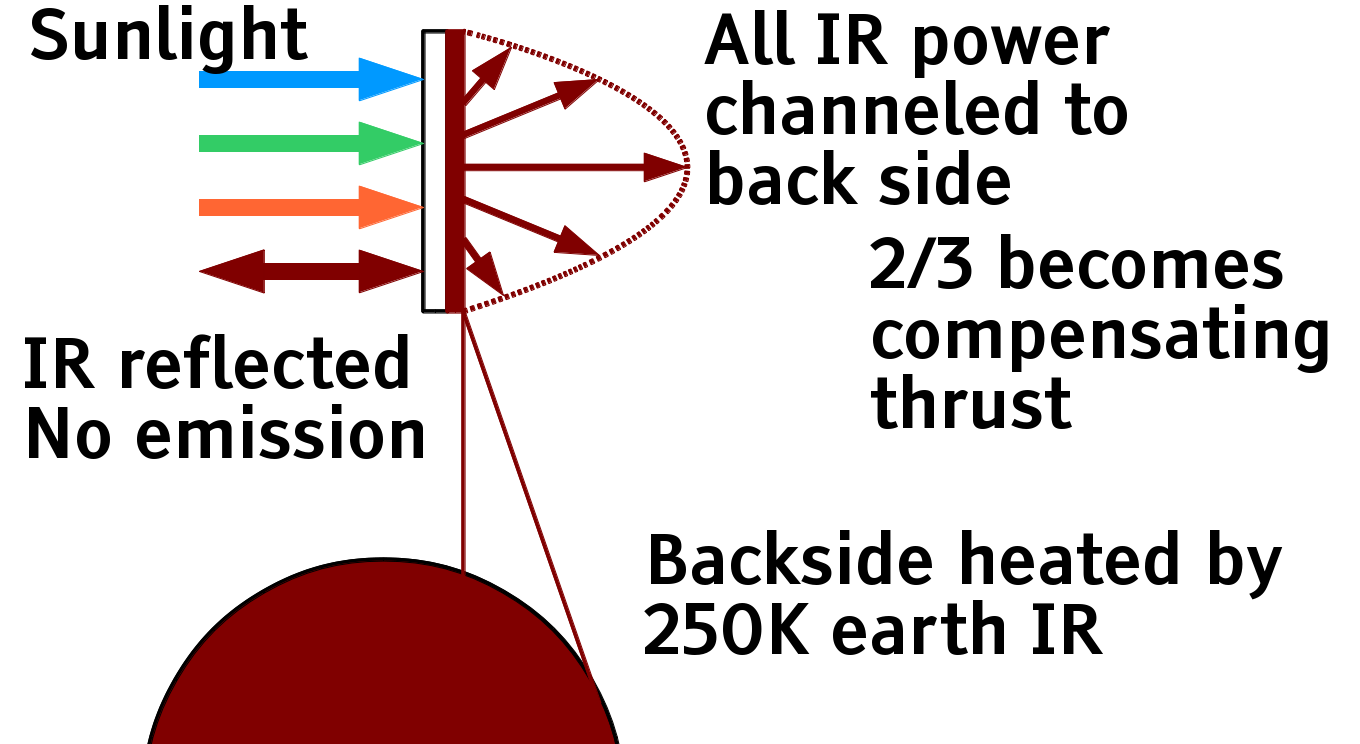
Infrared Bandpass Filtered Thinsats
|
Adding an optical high-pass filter to the front (sunwards) side of a thinsat allows almost all the high energy sunlight to reach the solar cells, while pushing all the black body thermal emissions to the back side. The infrared emissions create light pressure thrust that balances 2/3 of the front side thrust, reducing orbit-distorting light sail thrust to 1/3 of the thrust caused by light absorption on the solar cells in front. |
Backside Infrared Thrust
Solid angle is the two dimensional "angular area" of something projected onto a unit sphere. The solid angle of the whole sphere is 4π steradians;, the solid angle of a half-sphere is 2π steradians;, the solid angle of a 1 degree wide band around any circumference of the sphere is 4π sin( 0.5° ) ≅ 0.1097 ster . A 1° radius circle is 9.570E-4 ster, and the visual size of the earth seen from the m288 orbit, close to 30° radius, is 2π( 1-cos(30°) ) ≅ 0.8418 ster.
Black body radiation from a flat surface is Lambertian - the intensity of the radiation per solid angle observed is constant. Perpendicular to the surface, a disk appears round with maximum solid angle. At angle \theta from perpendicular, the disk appears just as "bright" but the disk appears elliptical; just as bright per solid angle, but the solid angle size is smaller. Lambertian radiation means the intensity of the solid angle is the same, it just looks smaller so less radiation comes at you as the angle increases, dropping to zero edge-on. The radiation intensity at angle \theta is I_0 \cos( \theta ) where I_0 is a constant we shall calculate now.
For a thin band with an angle of \theta and width d\theta, the solid angle receiving the radiation is 2 \pi \sin( \theta ) d\theta and the radiation received is 2 \pi I_0 \cos( \theta ) \sin( \theta ) d\theta , or \pi I_0 \cos( 2 \theta ) d\theta . The total power P is the integral of this for \theta between 0 and \pi/2, so P = \pi I_0 or I_0 = P/\pi .
The light pressure thrust is proportional to power divided by the speed of light c . Perpendicular emissions create a perpendicular thrust, thrust at right angles to the perpendicular creates zero perpendicular thrust, and thrust at angle \theta from the perpendicular creates \cos( \theta ) times the perpendicular thrust. The perpendicular thrust from the band an angle of \theta and width d\theta is dF = ( 2 \pi I_0 / c ) \cos( \theta )^2 \sin( \theta ) d\theta = ( 2 P / c ) \cos( \theta )^2 \sin( \theta ) d\theta . Again integrating for \theta between 0 and \pi/2, the total force F = 2P/3 c , 2/3 of the light pressure thrust if the thermal radiation all came perpendicularly out the back. While it would be nice to beam ALL the thrust backwards captured by the front, summing to a total thrust of zero, that is not thermodynamically possible. Reducing the sum of frontside and backside thrust to 1/3, and reducing launch mass in proportion, is still Very Nice.
Note to perpetual motion machinists: A beam of light has a property called Etendue (ay-tahn-doo), a measure of the disorganization of the beam. Perfectly collimated light has an etendue of zero, all the rays are parallel. Disorganized light leaves a surface with rays scattering in all directions, and has higher etendue. No combination of mirrors and lenses can reduce etendue of the whole beam, the quantity always increases. Black body radiation has maximum etendue; there's no way to focus it on a spot smaller than the emitting surface. If you could, that spot could be hotter than the source, violating the second law of thermodynamics.
Front side absorption and thrust versus IR filter energy cutoff
W/m² |
|
|
1366 |
sun power |
|
1347 |
emitted power |
|
1347 |
absorbed power |
|
19.1 |
reflected power |
|
8.9 |
IR power emitted frontside |
|
1338 |
IR power emitted backside |
|
499.1 |
forward thrust power |
|
573.7 |
photovoltaic illumination |
|
|
|
|
|
|
|
120°C |
Thinsat temperature |
|
0.87 |
thrust/photovoltaic ratio |
|
3.5 μm |
filter wavelength |
|
source . . gnuplot source |
||
MoreLater: A description of the midnight flip maneuver.
MoreLater: Absorbing heat from the earth during the night side flip.