Making Ballast from Rocket Tanks with Lasers

(work in progress)

Space debris is an opportunity, not a problem. Rocket tanks may be cut into gram-sized weights with lasers, then added to ultra-thinsats to stabilize their orbits against light pressure. The actual laser system must concentrate a lot of energy, conduct a lot of waste heat, and have enough mass to not drift relative to the workpiece in light pressure. Thinsats aren't the appropriate technology for this, and they can't work in high-drag LEO where most of the derelict mass is.

Thinsats are still useful for transport to MEO orbits. Ultra-thinsats (needing ballast) can be brought up with a small laser satellite, which makes rendezvous with a derelict rocket body, boosts it above the <2000km altitude high drag zone, then cuts ballast chunks off the rocket body tanks, dispenses an ultra-thinsat and attaches ballast, and sends it on its way. The ballasted thinsat may need a year or two to reach an M288 orbit from a Molniya orbit, but if thinsats can be made cheaply enough, that may be more cost efficient than adding another stage to move the derelict to a disassembly orbit near M288.

Whichever path is taken, the laser satellite's last task is to cut away its own tankage and no-longer-useful material, and make that into more ballast. The remaining laser and solar cell arrays will be useful for remote powered laser propulsion.

A Brief Discussion of Laser Cutting

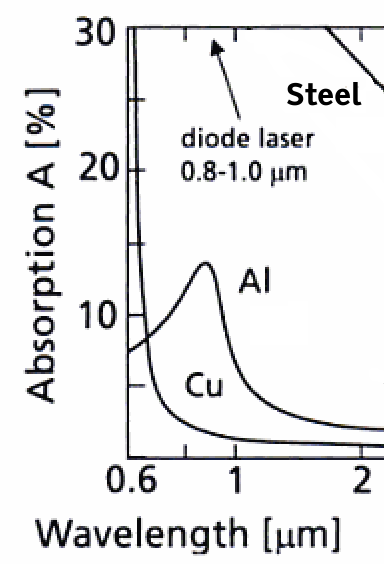
Rocket upper stage tanks have a thickness from 1 to 5 mm (Need Reference) and are typically aluminum alloy. Aluminum has an absorption peak of 14% around 900nm (LOOSEN1998). If we assume a 1cm² aperture emitter and a 1 meter distance, we can make a 10μm diameter ( 5μm radius) spot, maybe, given a magic phase-coherent focusing solid state laser. That is not available yet, but may be by the time we are processing derelicts.

Loosen's equation 2 offers this formula for beam-center intensity:

I_v \propto \Large { { T_v \kappa } \over { Abs ~ w_F ~ arctan \left( { { 8 \kappa t_L } \over { w_f^2 } } \right)^{{1}\over{2}} } }

The units in the above equation are wrong. I do not have access to Hans-Georg Treusch's 1985 thesis, but the units work out if instead we use the formula:

I_v \propto \Large { { T_v \lambda_{th} } \over { Abs ~ w_F ~ arctan \left( { { 8 \kappa t_L } \over { w_f^2 } } \right)^{{1}\over{2}} } }

Another clue suggesting an error in Dr. Loosen's 1999 paper (and perhaps carried over from Dr Treusch's thesis) is that he refers to W/cm², while MKS units are used in the definition of the symbols.

The revised formula yields an intensity I_v of 4e11 W/m² or 0.4W/μm². The pulse energy is the intensity I_v multiplied by spot area ( \pi w_f^2 ) and the pulse duration t_L :

E_{pulse} = \pi w_f^2 t_L I_v \propto \Large { { \pi T_v \lambda_{th} ~ w_f ~ t_L } \over { Abs ~ arctan \left( { { 8 ~ \kappa ~ t_L } \over { w_f^2 } } \right)^{{1}\over{2}} } }

That yields about 30 μJoules per pulse. However, a lot of mischief may be hidden in the proportionality. Also, the formula does not directly include the heat of vaporization nor the change in heat capacity with temperature. Let's assume we must provide 20MJ/kg to cleanly vaporize the aluminum in vacuum, and 200μJ pulses. If our lasers and pulsing system are 6% efficient, and we have 4 watts available per laser, we can make 1200 pulses per second, and remove 12μg of material per second, 7.2 milligrams per minute.

With a 10μm kerf through 5 mm aluminum, one meter of cut removes 135 milligrams of material, so we can cut a meter of material in about 20 minutes. The best case orientation for cutting a cylinder in half is with the cylinder perpendicular to the sun, surrounded by a ring of thinsats normal to the sun and firing lasers edgewise into a circumference of the cylinder. However, the thinsats will be accelerated by light pressure, and will not hold steady relative to the cylinder.

BIG PROBLEM: The rocket body is much more massive than the thinsats. They will get blown away by light pressure. They will need to anchor to the rocket body, crawling slowly (somehow) and carving off chunks and flying away with them.

MoreLater

Laser-cutter thinsats can be spaced perhaps 50 centimeters apart, so a small constellation of thinsats might cut a tank in half in 10 minutes. It will probably take much longer to separate the halves widely enough that we can send more thinsats into the fray, but eventually we have a bunch of widely separate 2cm² square, 5mm thick chunks, usable as 2.7 gram ballast weights.

If the kerf width must be increased (say because of poor optics), so is the pulse energy and energy per meter, slowing down cutting speed.

Example: Soyuz Molniya Third Stage

850 three stage Soyuz family rockets have been launched since 1966 (SOYUZ2006), mostly to launch Molniya satellites into high elliptical orbits. That is the most common booster/satellite combination in history, so far, so we will use it as an example. If server sky is successful, then future generations of the Dragon 9 third stage will become the most popular, but we can assume these stages will be specially built for laser disassembly to ballast. If we can cut up most of a Molniya third stage, we can probably disassemble anything else.

Assume the stage is in a Molniya orbit with a perigee of 500 km altitude (6880 km radius) and an apogee of 46290 kilometers radius. We need to deliver the ballast mass to the near-circular M288 orbit.

Task 1: Rendezvous

We have delivered the thinsat "disassembly crew" with a long electrodynamic tether, which we rendezvous with the derelict stage.

We cut the stage into two pieces, and attach the shroud parts onto the engine end. We can either boost the RD-0110 engine and complicated stuff into higher perigee orbit for eventual disassembly, or deorbit it with a terminator tether, perhaps after scavenging some of the angular momentum. Given the low ballistic coefficient of the thinsats, they must be attached to the tether at perigee in "thick" atmosphere, but can fly free above 2000 km altitude or so.

We

Task 2: Slice off the engine end of the stage

Worst case, assume a gap between the tank and the shell. We will probably have to peel off a circumferential strip of shell to open a gap to cut the inner tank through. So, we will need to make two 8.36 m circumferential cuts, worst case one after the other, and with an array of laser-cutting thinsats that will take about 10 minutes, and another 5 minutes for the inner cut. We end up with a "rocket end" weighing 600 kg, and shell end weighing about 1800 kg.

Lower the rocket end to the bottom of the tether, and "upper" the tank end to the top of the tether. Tidal forces will do this, and if we do this at the proper rates, the ends of the tether will remain approximately radial to the earth.

If we simultaneously do this for the entire 6.7 meters of the rocket, leaving the RD-0110 engines as a special problem, we will have 12 donuts of tank and metal averaging around 150 kg each. How to separate them?

Perhaps with laser ablation thrust. We do not need precision for this, just blow off some of the metal. With perhaps 10,000 thinsats working on the problem, we can blow off 4 grams of material per second, 1/3 gram per second per 150 kg object. The aluminum will have a thermal velocity of \sqrt( { k 3000K / m_AL } , k = Boltzmann constant = 1.38e-23 J/K, m_AL = ( 27 / 6.02e26 ) = 4.48e-26 kg, for a velocity of 960 meters per second sprayed in a half-sphere direction, an average of 480 meters per second perpendicular to the ablating surface. The thrust will be 0.16 newtons, accelerating donuts at about 1 mm/s². That can separate the donuts to 20 meters distance and stop them in less than 5 minutes. We can continue the cutting and separation process until we've taken the tanks apart

MoreLater