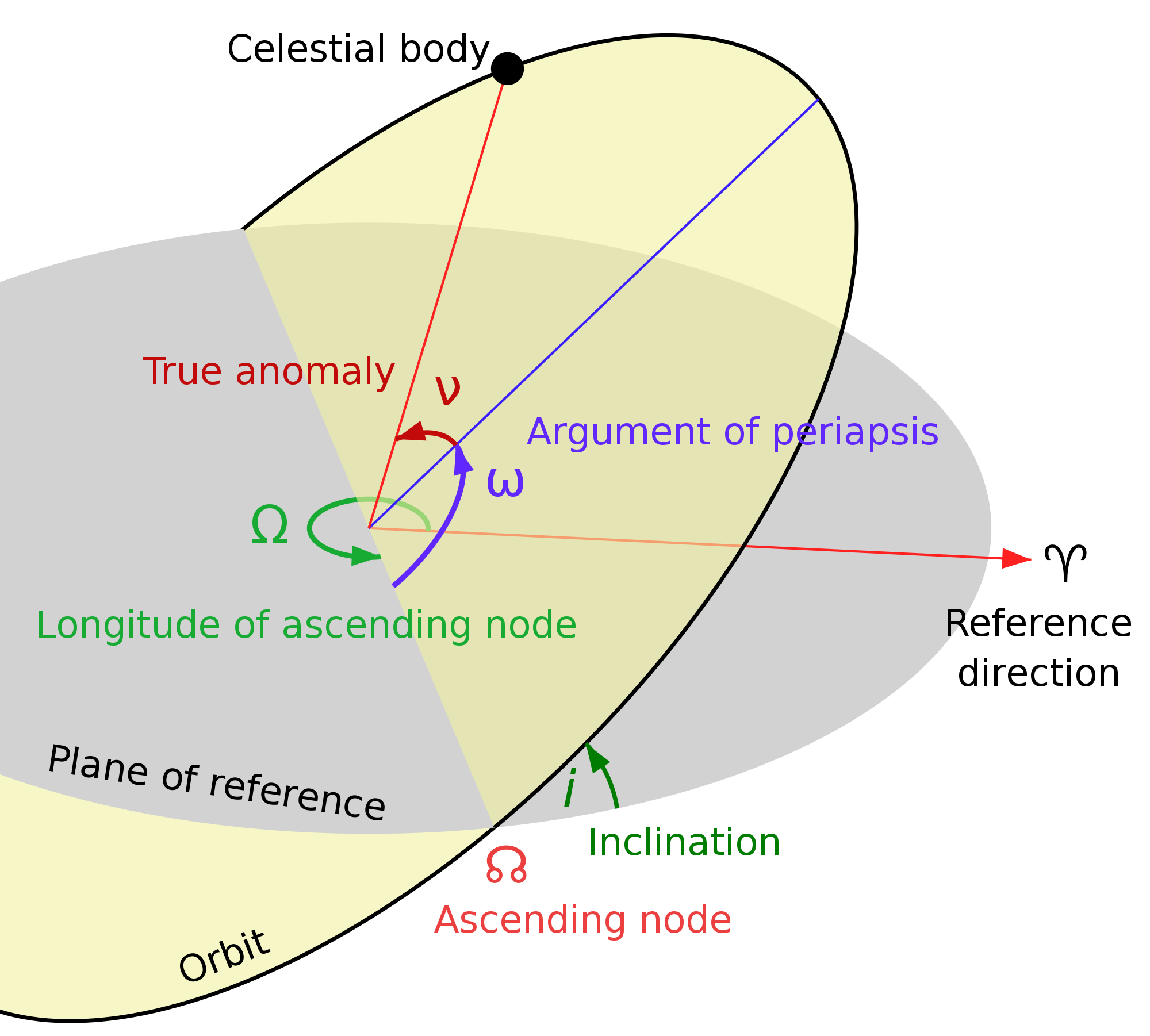
Changing Orbits to M288
How do we get from any arbitrary orbit to M288? The following techniques may not be optimal for minimal \Delta V , but they set an upper bound. We will assume Kepler orbits and a circular M288 destination orbit, and heavy objects unaffected by light pressure. Actual thinsat orbits are elliptical and precess over a year with J2 and light pressure.
The origin elliptical Kepler orbit has four parameters we need to compute two \Delta V burns for our transfer orbit: |
Maneuvers use the least \Delta V farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit r_{288} .
Describing an arbitrary Kepler orbit
Blue curve: |
Red curve: |
Green curve: |
orb01.pngorb02.pngorb04.pnggnuplot source and you will need to crop and convert and resize using gimp to reproduce the above images.
\mu |
earth gravitational constant |
3.986004418e14 m3/s2 |
|
T |
sidereal orbital period (s) |
||
a |
semimajor axis (m) |
0.5 ( r_a + r_p ) |
\large \left( \mu \left( T \over { 2 \pi } \right)^2 \right)^{1/3} |
e |
eccentricity (unitless) |
\Large { { r_a } \over { a } } - 1 |
\Large { { r_a - r_p } \over { r_a + r_p } } |
r_p |
perigee, periapsis (m) |
a ( 1 - e ) |
|
r_a |
apogee, apoapsis (m) |
a ( 1 + e ) |
|
v_o |
orbit velocity (m/s) |
\large \sqrt{ \mu ( 1 - e^2 ) / a } |
|
v_p |
perigee velocity (m/s) |
( 1 + e ) v_0 |
|
v_a |
apogee velocity (m/s) |
( 1 - e ) v_0 |
|
\theta |
true anomaly, orbit angle from perigee |
radians or degrees |
|
r |
radius (m) |
\large a ( 1 - e^2 ) / ( 1 + e \cos( \theta ) ) |
|
v_{\perp} |
velocity perpendicular to radius (m/s) |
\large v_0 ( 1 + e \cos( \theta ) ) |
|
v_r |
radial velocity (m/s) |
\large e v_0 \sin( \theta ) |
|
\omega |
argument of perigee, radians |
||
i |
inclination, radians |
Orbits in V-H coordinates
We are interested in delivering an object from an arbitrary starting orbit to M288, and the \Delta V impulses necessary. First we will describe the orbit in radial coordinates ( V, H ), then compute the two impulses:
- 1. plane change to a temporary equatorial orbit with an apogee or perigee at the M288 orbit, then
- 2. insertion into M288 circular orbit
There may be more optimal strategies, and we may use non-traditional propulsion systems like VASIMR engines or tethers to accomplish the \Delta V , but the calculations are easier in bulk if we treat all 10,000+ objects in the NORAD catalog the same way. Although I can't share the whole catalog here, you can sign up for it, and I will risk sharing some data for the hundreds of SL-6 Molniya third stage rocket bodies, which threaten the M288 orbits and whose aluminum tanks can provide many tons of ballast for server sky.
Let's do the math in Cartesian (x,y,z) coordinates. The z component is in the direction of the earth's north pole, with the x and y components confined to the equatorial plane.
Start with the basic Kepler orbit with the argument of perigee \omega (the angle from the x axis), in the equatorial plane:
r_1 = \large a_1 ( 1 - {e_1}^2 ) / ( 1 + {e_1} \cos( \theta ) )
v_{\perp 1} = \large v_{01} ( 1 + {e_1} \cos( \theta ) )
v_{radial 1} = \large e v_{01} \sin( \theta )
MORE DERIVATION LATER
The orbit crosses the equatorial plane where \theta = \omega and \theta = \pi + \omega . Thus:
r_1 = \large a_1 ( 1 - {e_1}^2 ) / ( 1 \pm {e_1} \cos( \omega ) ) V = 0
v_{01}= \large \sqrt{ \mu ( 1 - e^2 ) / a }
v_{\perp 1} = \large v_{01} ( 1 \pm {e_1} \cos( \omega ) )
v_{radial 1} = \large \pm e v_{01} \sin( \omega )
Because of the inclination i , the perpendicular velocity is out-of-plane, and has a Z (north-south) and an H (in-plane) component, like so:
v_{H 1} = \large v_01 \cos( i ) ( 1 \pm {e_1} \cos( \omega ) )
v_{V 1} = \large v_01 \sin( i ) ( 1 \pm {e_1} \cos( \omega ) )
Our goal is to add a \Delta V_1 , and end up with a velocity vector that is perigee (or apogee) of an elliptical equatorial orbit whose apogee (or perigee) is at M288, where we add \Delta V_2 and end up in a circular M288 orbit. We will choose the orbital pass and time the transfer so we pass through a gap in the M288 constellation. The constellation of light-pressured thinsats will be an elliptical orbit wrapped around the central, circular M288 orbit, so we will likely be able to pass "over or under" the elliptical orbit in the equatorial plane. That orbit is defined by:
a_2 = ( r_1 + r_{288} ) / 2 ;
e_2 = {r_1}/{a_2} - 1 e_2 may be negative
v_{H 2} = ( 1 - e_2 ) \sqrt{ \mu ( 1 - {e_2}^2 ) / {a_2} }
v_{V 2} = 0
v_{radial_2} = 0
The velocity change at r_1 is :
\Delta V_{H} = v_{H 2} - v_{H 1}
\Delta V_{V} = - v_{H 1}
\Delta V_{radial} = -v_{radial_1}
The total \Delta V_1 is the vector sum of those three orthogonal vector components.
The orbit insertion into the final orbit is simple - a thrust along the orbit path at (perigee/apogee), changing velocity from V_{H 3} (the velocity of the incoming orbit) to V_{M288} .
v_{H 3} = ( 1 + e_2 ) \sqrt{ \mu ( 1 - {e_2}^2 ) / {a_2} }
v_{M288} = \large \sqrt{ \mu / r_{M288} }
\Delta V_2 = v_{M288} - v_{H 3}
There are TWO possible starting positions and velocities to perform this calculation on, with two possible pairs of \Delta V . We can choose either pair, based on the smallest scalar total \Delta V , the smallest \Delta V_1 , the smallest \Delta V_2 , or some weighted average based on the technologies used. We may discard portions of the rocket body, perhaps throwing them towards reentry in a way that provides useful \Delta V .
Molniya Rocket Body Transfer
More than one hundred SL-6 third stage rocket bodies remain in orbit after placing Molniya satellites into 12 hour, high eccentricity, high inclination orbits that dwell above northern Asia. Most of these can reach M288 with less than 4 km/s of \Delta V , even though the high inclination means big plane changes.
These high orbit rocket bodies are collision hazards, but will be difficult to capture and re-enter with rockets or electrodynamic tethers. Fortunately, the tank portions can be cut into 1 to 10 gram ballasts for ultra-light (< 50g/m2) server sky thinsats. That weight stabilizes thinsat orbits, so their orbits are not as perturbed by light pressure. Every gram of ballast replaces a kilogram launched and placed into M288 orbit.
The Commonwealth of Independent States (CIS, most of the former Soviet Union) has vague liability for these, as well as vague ownership. It would be wonderful if server-sky could turn these liabilities into assets that the CIS member states could sell. There are 600+ other rocket bodies in similar orbits, so the CIS would not have a monopoly, but at a thousand dollars per kilogram for ballast, a $100 million dollar windfall for these countries would be welcome, compared to hundreds of millions of dollars of liability of they collide with a valuable operating satellite. There will be additional value from launching the space tugs and argon fuel that matches orbits with these bodies; these orbits are designed to be reached from the launch centers at Baikonur and Plesetsk.
Rocket Bodies versus Delta V
In January 2013, there were 1600+ abandoned rocket bodies in orbit:
LEO Rocket Bodies |
812 |
High Orbit Rocket Bodies |
838 |
Soyuz-Molniya / SL-6 |
112 |
Total CIS Rocket Bodies |
1016 |
Other Rocket Bodies |
634 |
Total Rocket Bodies |
1650 |
Debris |
9998 |
Total Objects |
15022 |
Here's two plots for the 1600+ rocket bodies in orbit, with the second focused on rocket bodies with less than 6.5 km/s \Delta V to M288. "LEO" means rocket bodies with a semimajor axis of less than 2000+6371 km - that could mean a perigee of 300km and an apogee of 3700km altitude.
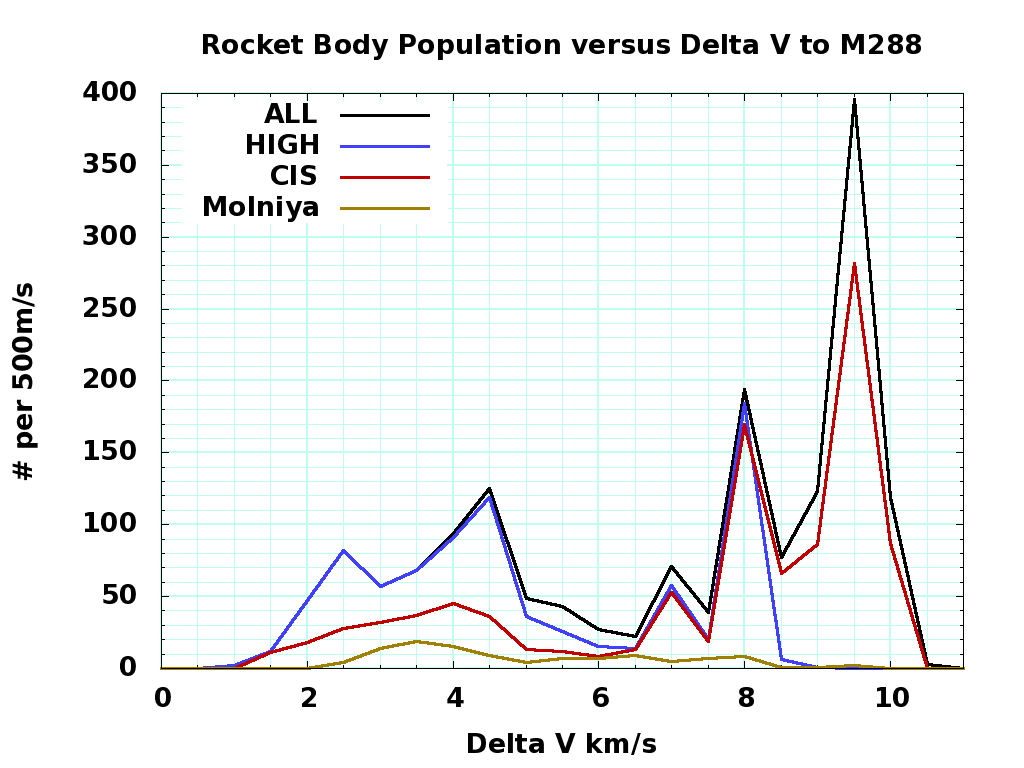
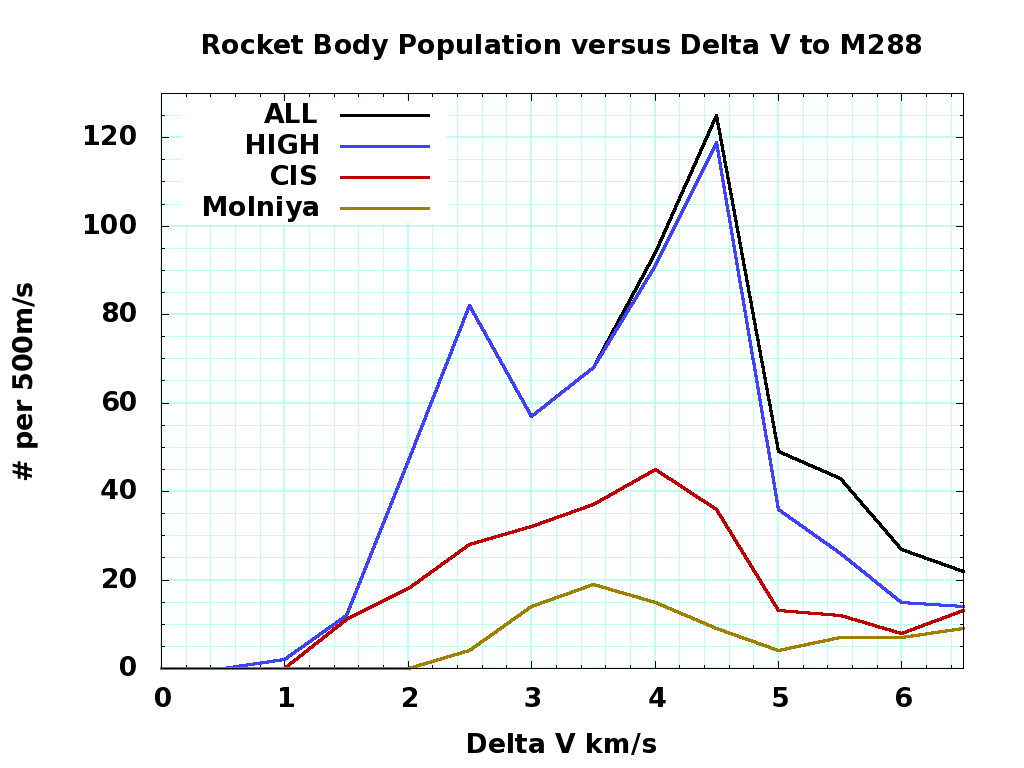
Sorry, I can't give you the January 26, 2013 3-line element catalog I made this from. Please register for an account at http://space-track.org
VASIMR
Those space tugs might be VASIMR engine powered. A VASIMR engine is about 60% energy efficient, producing 40km/sec exhaust from argon (an inert gas making up 0.93% of the atmosphere. So a 100 kilowatt array will produce 60 kilowatts of exhaust kinetic energy, consume 75 micrograms of argon per second, and produce 3 newtons of thrust. For a 1.4 tonne rocket body and a 1.6 ton engine/solar array/fuel-tank orbital tug, that is 3.6 meters per second per hour acceleration and 0.27 kg/hr argon usage. The tug can add 4000 m/s of \Delta V in about two months (WAG), using 300kg of argon, and without a payload, maneuver towards the next rocket body with half the time and fuel, perhaps to rendezvous first with a few hundred kilograms of extra fuel sent from the ground. The resupply tanks and space tugs themselves can be broken up for ballast as they age or become obsolete.
VASIMR engines are still under development. They have problems with DC-to-RF energy conversion, and waste heat elimination. The superconducting coils, and refillable cryogenic argon tanks that will not leak for years, will be challenging. However, distributed design may help. For example, we can cover the tanks with temperature shielding and solar cells, and orient them towards the sun, perhaps balancing them well enough that VASIMR micro thrusters can make up for the long term accumulation of torque that momentum wheels cannot correct. Similarly, rather than pipe DC current to an RF converter box, it may be more efficient to convert to RF energy at the solar arrays, and ship microwaves down waveguides or even quadrature balanced striplines ( GND signal+ SIGNAL- SIGNAL+ signal- GND ) so that waste heat from conversion losses are dissipated away from the argon supply. Let's assume the VASIMR designers are smart and can improve their designs over the next decade.
We will only produce power and thrust during part of the orbit. The rest of the time, we can use the solar cell power output for solid state cryo-coolers, or for cutting lasers to begin the process of cutting up the rocket bodies.