|
Size: 3500
Comment:
|
Size: 3559
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 18: | Line 18: |
| || $ T $ || sidereal orbital period (s) || $ { 2 \pi } \over \omega $ || || $ a $ || semimajor axis (m) || $ 0.5 ( r_a + r_p ) $ || $ \left( \mu \left( T \over { 2 \pi } \right)^2 \right)^{1/3} || || $ e $ || eccentricity (unitless) || $ { { r_a } \over { a } } ~-~ 1 $ || $ { { r_a - r_p } \over { r_a + r_[ } } $ || |
|| $ T $ || sidereal orbital period (s) || $ \Large { { 2 \pi } \over \omega } $ || || $ a $ || semimajor axis (m) || $ 0.5 ( r_a + r_p ) $ || $ \large \left( \mu \left( T \over { 2 \pi } \right)^2 \right)^{1/3} $ || || $ e $ || eccentricity (unitless) || $ \Large { { r_a } \over { a } } - 1 $ || $ \Large { { r_a - r_p } \over { r_a + r_p } } $ || |
| Line 23: | Line 23: |
| || $ v_o $ || orbit velocity (m/s) || $ \sqrt{ \mu ( 1 - e^2 ) / a } $ || | || $ v_o $ || orbit velocity (m/s) || $ \large \sqrt{ \mu ( 1 - e^2 ) / a } $ || |
| Line 27: | Line 27: |
| || $ r $|| radius (m) || $ a ( 1 - e^2 ) / ( 1 + e \cos( \theta ) ) $ || ||$v_{\perp}$|| velocity perpendicular to radius (m/s) || $ v_0 ( 1 + e \cos( \theta ) ) $ || || $ v_r $ || radial velocity (m/s) || $ e v_0 \sin( \theta ) $ || |
|| $ r $|| radius (m) || $ \large a ( 1 - e^2 ) / ( 1 + e \cos( \theta ) ) $ || ||$v_{\perp}$|| velocity perpendicular to radius (m/s) || $ \large v_0 ( 1 + e \cos( \theta ) ) $ || || $ v_r $ || radial velocity (m/s) || $ \large e v_0 \sin( \theta ) $ || |
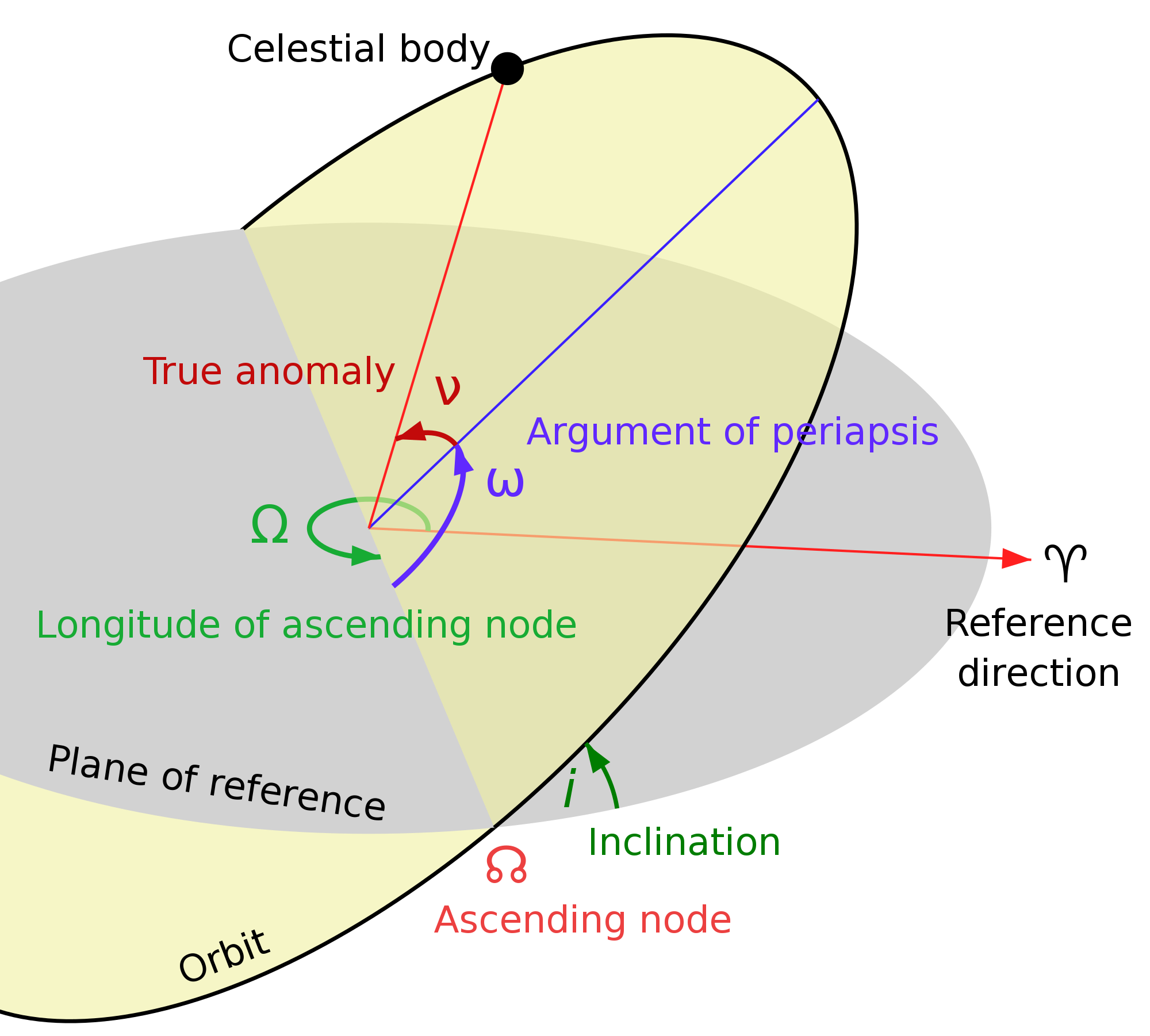
Changing Orbits to M288
How do we get from any arbitrary orbit to M288? The following techniques may not be optimal for minimal \Delta V , but they set an upper bound. We will assume Kepler orbits and a circular M288 destination orbit, and heavy objects unaffected by light pressure. Actual thinsat orbits are elliptical and precess over a year with J2 and light pressure.
The origin elliptical Kepler orbit has four parameters we need to compute two \Delta V burns for our transfer orbit: |
Maneuvers use the least \Delta V farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit r_288 .
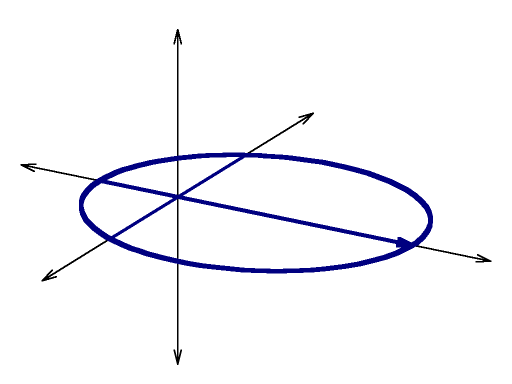
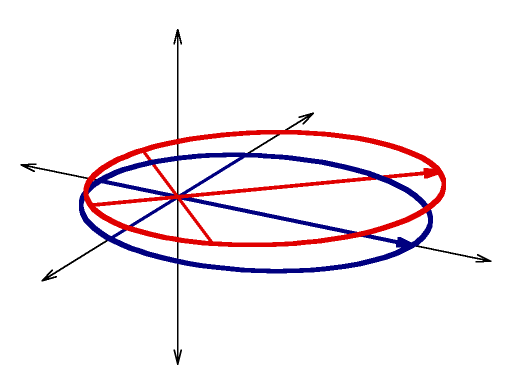
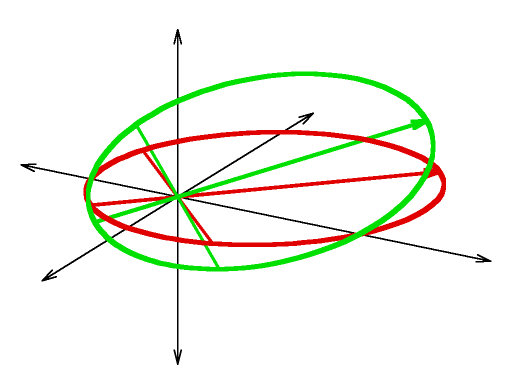
Describing an arbitrary Kepler Orbit
Blue curve: |
|
Red curve: |
|
Green curve: |
gnuplot source and you will need to crop and convert and resize using gimp to reproduce the above images.
\mu |
earth gravitational constant |
3.986004418e14 m3/s2 |
|
T |
sidereal orbital period (s) |
\Large { { 2 \pi } \over \omega } |
|
a |
semimajor axis (m) |
0.5 ( r_a + r_p ) |
\large \left( \mu \left( T \over { 2 \pi } \right)^2 \right)^{1/3} |
e |
eccentricity (unitless) |
\Large { { r_a } \over { a } } - 1 |
\Large { { r_a - r_p } \over { r_a + r_p } } |
r_p |
perigee, periapsis (m) |
a ( 1 - e ) |
|
r_a |
apogee, apoapsis (m) |
a ( 1 + e ) |
|
v_o |
orbit velocity (m/s) |
\large \sqrt{ \mu ( 1 - e^2 ) / a } |
|
v_p |
perigee velocity (m/s) |
( 1 + e ) v_0 |
|
v_a |
apogee velocity (m/s) |
( 1 - e ) v_0 |
|
\theta |
true anomaly, orbit angle from perigee |
radians or degrees |
|
r |
radius (m) |
\large a ( 1 - e^2 ) / ( 1 + e \cos( \theta ) ) |
|
v_{\perp} |
velocity perpendicular to radius (m/s) |
\large v_0 ( 1 + e \cos( \theta ) ) |
|
v_r |
radial velocity (m/s) |
\large e v_0 \sin( \theta ) |
MORE LATER