|
Size: 3559
Comment:
|
Size: 5497
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 18: | Line 18: |
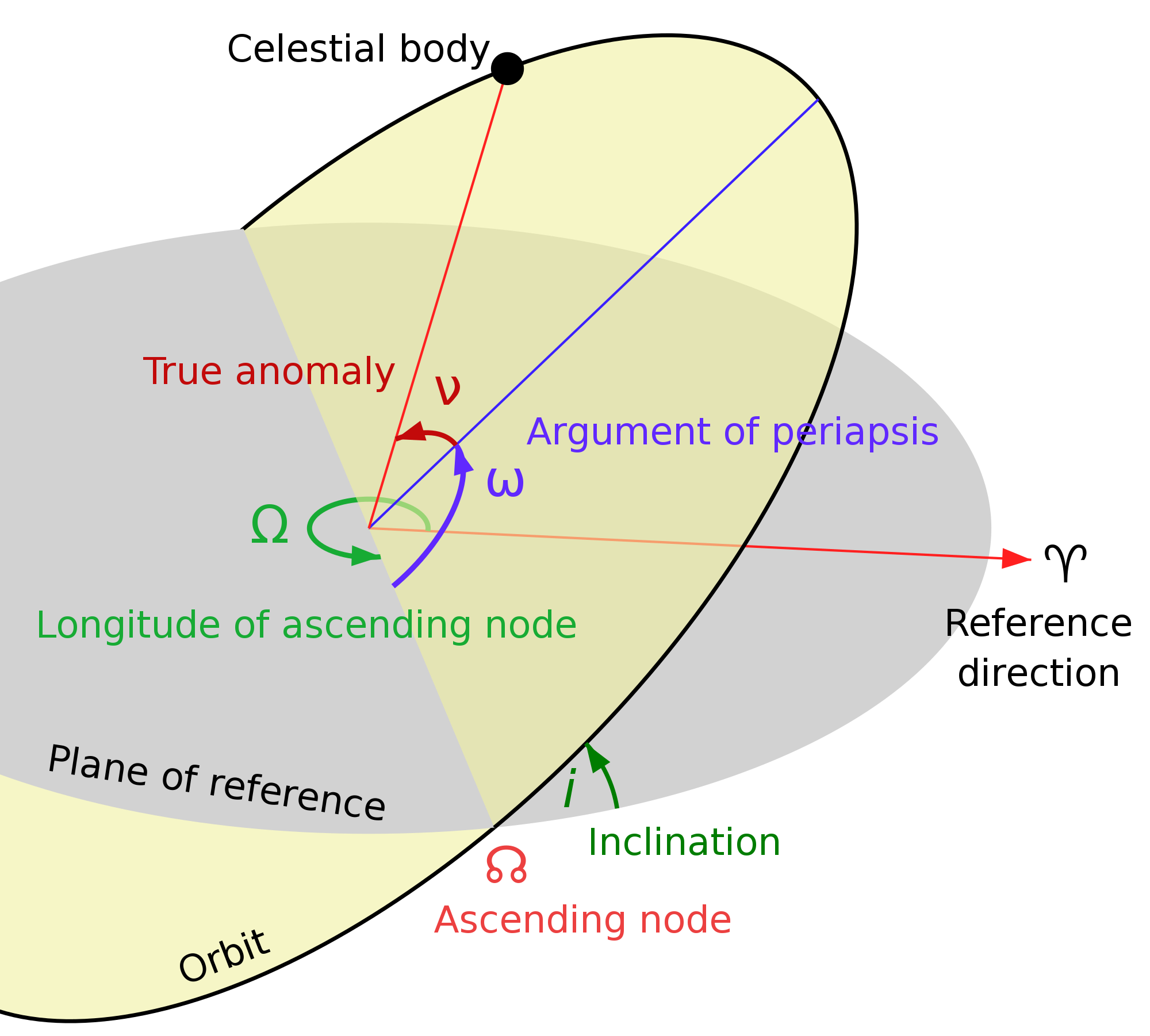
| || $ T $ || sidereal orbital period (s) || $ \Large { { 2 \pi } \over \omega } $ || | || $ T $ || sidereal orbital period (s) || |
| Line 30: | Line 30: |
| || $ \omega $|| argument of perigee, radians || || $ i $ || inclination, radians || === Orbits in V-H coordinates === We are interested in delivering an object from an arbitrary starting orbit to M288, and the $ \Delta V $ impulses necessary. First we will describe the orbit in radial coordinates ( V, H ), then compute the two impulses: .1. plane change to a temporary equatorial orbit with an apogee or perigee at the M288 orbit, then .2. insertion into M288 circular orbit There may be more optimal strategies, and we may use non-traditional propulsion systems like VASIMR engines or tethers to accomplish the $ \Delta V $, but the calculations are easier in bulk if we treat all 10,000+ objects in the NORAD catalog the same way. Although I can't share the whole catalog here, you can sign up for it, and I will risk sharing some data for the hundreds of SL-6 Molniya third stage rocket bodies, which threaten the M288 orbits and whose aluminum tanks can provide many tons of ballast for server sky. Let's do the math in Cartesian (x,y,z) coordinates. The z component is in the direction of the earth's north pole, with the x and y components confined to the equatorial plane. Start with the basic Kepler orbit with the argument of perigee $ \omega $ (the angle from the x axis), in the equatorial plane: . $ r_1 = \large a_1 ( 1 - {e_1}^2 ) / ( 1 + {e_1} \cos( \theta ) ) $ . $ v_{\perp 1} = \large v_01 ( 1 + {e_1} \cos( \theta ) ) $ . $ v_{r 1} = \large e v_01 \sin( \theta ) $ Now include the argument of perigee $ \omega $ (a rotation around the z axis): . $ r_1 = \large a_1 ( 1 - {e_1}^2 ) / ( 1 + {e_1} \cos( \theta - \omega ) ) $ . $ v_{\perp 1} = \large v_01 ( 1 + {e_1} \cos( \theta - \omega ) ) $ . $ v_{r 1} = \large e v_01 \sin( \theta - \omega ) $ Dividing these into Cartesian coordinates: . $ x_1 = $ . $ y_1 = $ . $ z_1 = 0 $ . $ vx_1 = $ . $ vy_1 = $ . $ vz_1 = 0 $ |
|
| Line 32: | Line 65: |
| MORE LATER |
Changing Orbits to M288
How do we get from any arbitrary orbit to M288? The following techniques may not be optimal for minimal \Delta V , but they set an upper bound. We will assume Kepler orbits and a circular M288 destination orbit, and heavy objects unaffected by light pressure. Actual thinsat orbits are elliptical and precess over a year with J2 and light pressure.
The origin elliptical Kepler orbit has four parameters we need to compute two \Delta V burns for our transfer orbit: |
Maneuvers use the least \Delta V farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit r_288 .
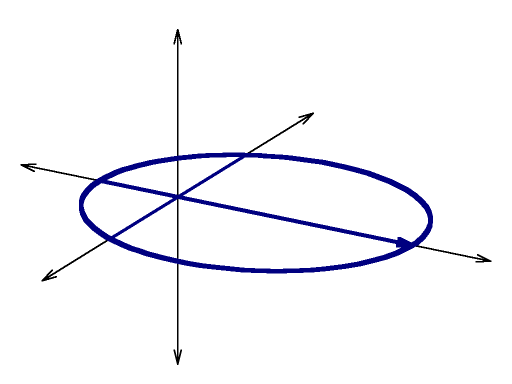
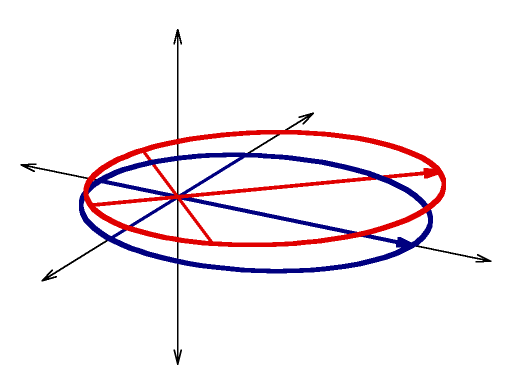
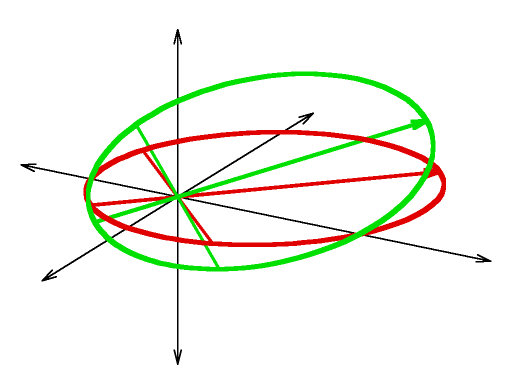
Describing an arbitrary Kepler Orbit
Blue curve: |
|
Red curve: |
|
Green curve: |
gnuplot source and you will need to crop and convert and resize using gimp to reproduce the above images.
\mu |
earth gravitational constant |
3.986004418e14 m3/s2 |
|
T |
sidereal orbital period (s) |
||
a |
semimajor axis (m) |
0.5 ( r_a + r_p ) |
\large \left( \mu \left( T \over { 2 \pi } \right)^2 \right)^{1/3} |
e |
eccentricity (unitless) |
\Large { { r_a } \over { a } } - 1 |
\Large { { r_a - r_p } \over { r_a + r_p } } |
r_p |
perigee, periapsis (m) |
a ( 1 - e ) |
|
r_a |
apogee, apoapsis (m) |
a ( 1 + e ) |
|
v_o |
orbit velocity (m/s) |
\large \sqrt{ \mu ( 1 - e^2 ) / a } |
|
v_p |
perigee velocity (m/s) |
( 1 + e ) v_0 |
|
v_a |
apogee velocity (m/s) |
( 1 - e ) v_0 |
|
\theta |
true anomaly, orbit angle from perigee |
radians or degrees |
|
r |
radius (m) |
\large a ( 1 - e^2 ) / ( 1 + e \cos( \theta ) ) |
|
v_{\perp} |
velocity perpendicular to radius (m/s) |
\large v_0 ( 1 + e \cos( \theta ) ) |
|
v_r |
radial velocity (m/s) |
\large e v_0 \sin( \theta ) |
|
\omega |
argument of perigee, radians |
||
i |
inclination, radians |
Orbits in V-H coordinates
We are interested in delivering an object from an arbitrary starting orbit to M288, and the \Delta V impulses necessary. First we will describe the orbit in radial coordinates ( V, H ), then compute the two impulses:
- 1. plane change to a temporary equatorial orbit with an apogee or perigee at the M288 orbit, then
- 2. insertion into M288 circular orbit
There may be more optimal strategies, and we may use non-traditional propulsion systems like VASIMR engines or tethers to accomplish the \Delta V , but the calculations are easier in bulk if we treat all 10,000+ objects in the NORAD catalog the same way. Although I can't share the whole catalog here, you can sign up for it, and I will risk sharing some data for the hundreds of SL-6 Molniya third stage rocket bodies, which threaten the M288 orbits and whose aluminum tanks can provide many tons of ballast for server sky.
Let's do the math in Cartesian (x,y,z) coordinates. The z component is in the direction of the earth's north pole, with the x and y components confined to the equatorial plane.
Start with the basic Kepler orbit with the argument of perigee \omega (the angle from the x axis), in the equatorial plane:
r_1 = \large a_1 ( 1 - {e_1}^2 ) / ( 1 + {e_1} \cos( \theta ) )
v_{\perp 1} = \large v_01 ( 1 + {e_1} \cos( \theta ) )
v_{r 1} = \large e v_01 \sin( \theta )
Now include the argument of perigee \omega (a rotation around the z axis):
r_1 = \large a_1 ( 1 - {e_1}^2 ) / ( 1 + {e_1} \cos( \theta - \omega ) )
v_{\perp 1} = \large v_01 ( 1 + {e_1} \cos( \theta - \omega ) )
v_{r 1} = \large e v_01 \sin( \theta - \omega )
Dividing these into Cartesian coordinates:
x_1 =
y_1 =
z_1 = 0
vx_1 =
vy_1 =
vz_1 = 0