Differences between revisions 5 and 7 (spanning 2 versions)

Changing Orbits to M288

How do we get from any arbitrary orbit to M288? The following techniques may not be optimal for minimal \Delta V , but they set an upper bound. We will assume Kepler orbits and a circular M288 destination orbit, and heavy objects unaffected by light pressure. Actual thinsat orbits are elliptical and precess over a year with J2 and light pressure.

The origin elliptical Kepler orbit has four parameters we need to compute two \Delta V burns for our transfer orbit:

* Apogee r_a

* Perigee r_p

* Inclination i

* argument of perigee \omega

We can compute the semimajor axis a and the eccentricity e from the apogee and perigee

The angle of the ascending and descending nodes do not affect the \Delta V burns, though they do affect when we make our burns so we insert into the desired destination region of the M288 orbit.

Maneuvers use the least \Delta V farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit r_288 .

Describing an arbitrary Kepler Orbit

Blue curve: An orbit in the horizontal X,Y plane apogee = apoapsis = 6 perigee= periapsis = 2 semimajor axis = 4 eccentricity = 0.5
Red curve: A similar orbit with a 45 degree argument of perigee (rotate around vertical Z axis):
Green curve: A similar orbit with a 30 degree inclination (rotate around horizontal X axis): note that the ascending and descending nodes, where the orbit crosses the equatorial plane, do not have the same radius from the origin

gnuplot source and you will need to crop and convert and resize using gimp to reproduce the above images.

MORE LATER

-  ⇤ ← Revision 5 as of 2013-01-21 22:01:34 → 
  Size: 1460
  Editor: KeithLofstrom
  Comment:
+   ← Revision 7 as of 2013-01-21 23:39:26 → ⇥
  Size: 2215
  Editor: KeithLofstrom
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 4:
 How do we get from any arbitrary orbit to M288?   The following techniques may not be optimal for minimal $ \Delta V $, but they set an upper bound.  We will assume Kepler orbits and a circular M288 destination orbit, and heavy objects unaffected by light pressure.  Actual thinsat orbits are elliptical and precess over a year with J2 and light pressure.
 Line 8:
-Manuevers use the least $ \Delta V $ farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit $ r_288 $.
+Maneuvers use the least $ \Delta V $ farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit $ r_288 $.
 Line 12:
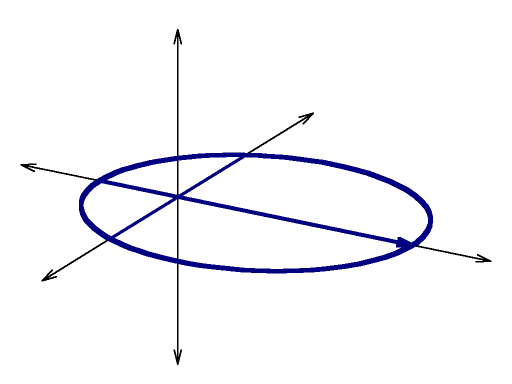
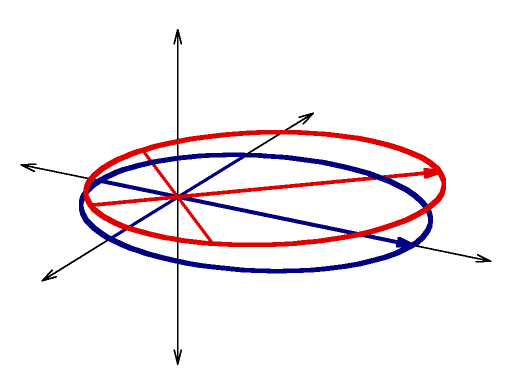
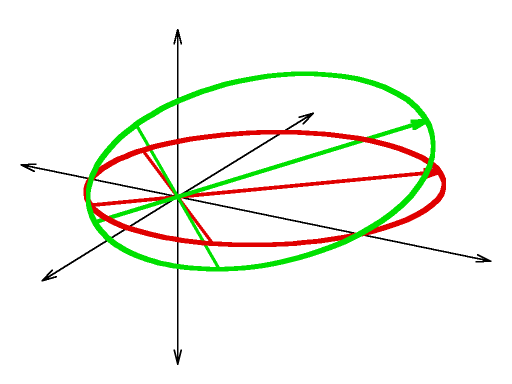
-|| Assume an x,y,z coordinate space and an orbit in the x,z plane: || {{ attachment:orb01.png | | }} ||
+|| Blue curve:<<BR>><<BR>>An orbit in the horizontal X,Y plane<<BR>><<BR>>apogee = apoapsis = 6<<BR>>perigee= periapsis = 2<<BR>>semimajor axis = 4<<BR>>eccentricity = 0.5 || {{ attachment:orb01.png | |width=256 }} ||
|| Red curve:<<BR>><<BR>>A similar orbit with a 45 degree '''argument of perigee''' <<BR>><<BR>>(rotate around vertical Z axis): || {{ attachment:orb02.png | |width=256 }} ||
|| Green curve:<<BR>><<BR>>A similar orbit with a 30 degree '''inclination''' <<BR>><<BR>>(rotate around horizontal X axis):<<BR>><<BR>><<BR>>note that the ascending and descending nodes, where the orbit crosses the equatorial plane, do not have the same radius from the origin|| {{ attachment:orb04.png | |width=256 }} ||
[[attachment:orb0.gp|gnuplot source]] and you will need to crop and convert and resize using gimp to reproduce the above images.

MORE LATER

Diff for "OrbitChange"

Changing Orbits to M288

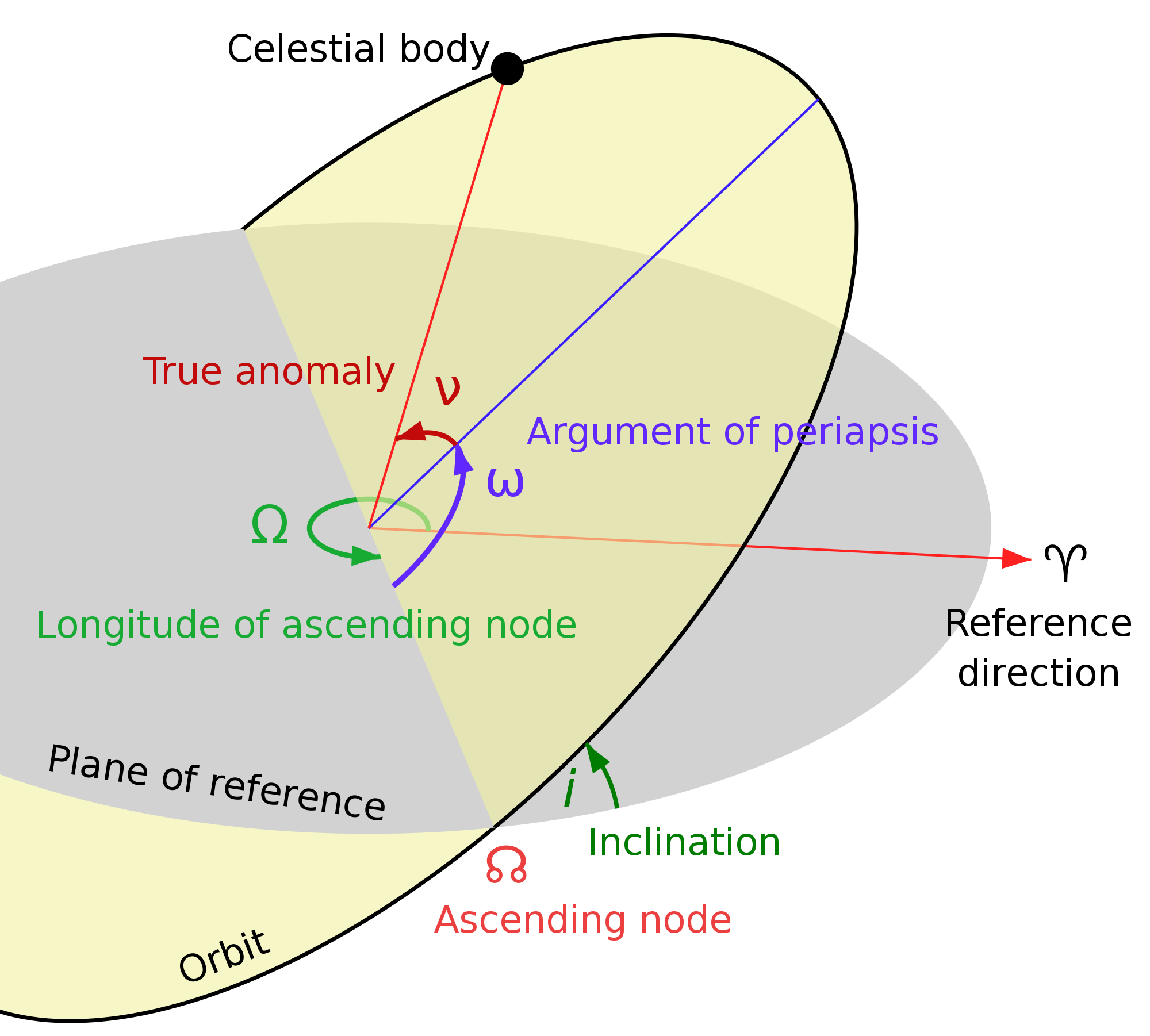
Describing an arbitrary Kepler Orbit