|
Size: 2215
Comment:
|
Size: 2215
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 6: | Line 6: |
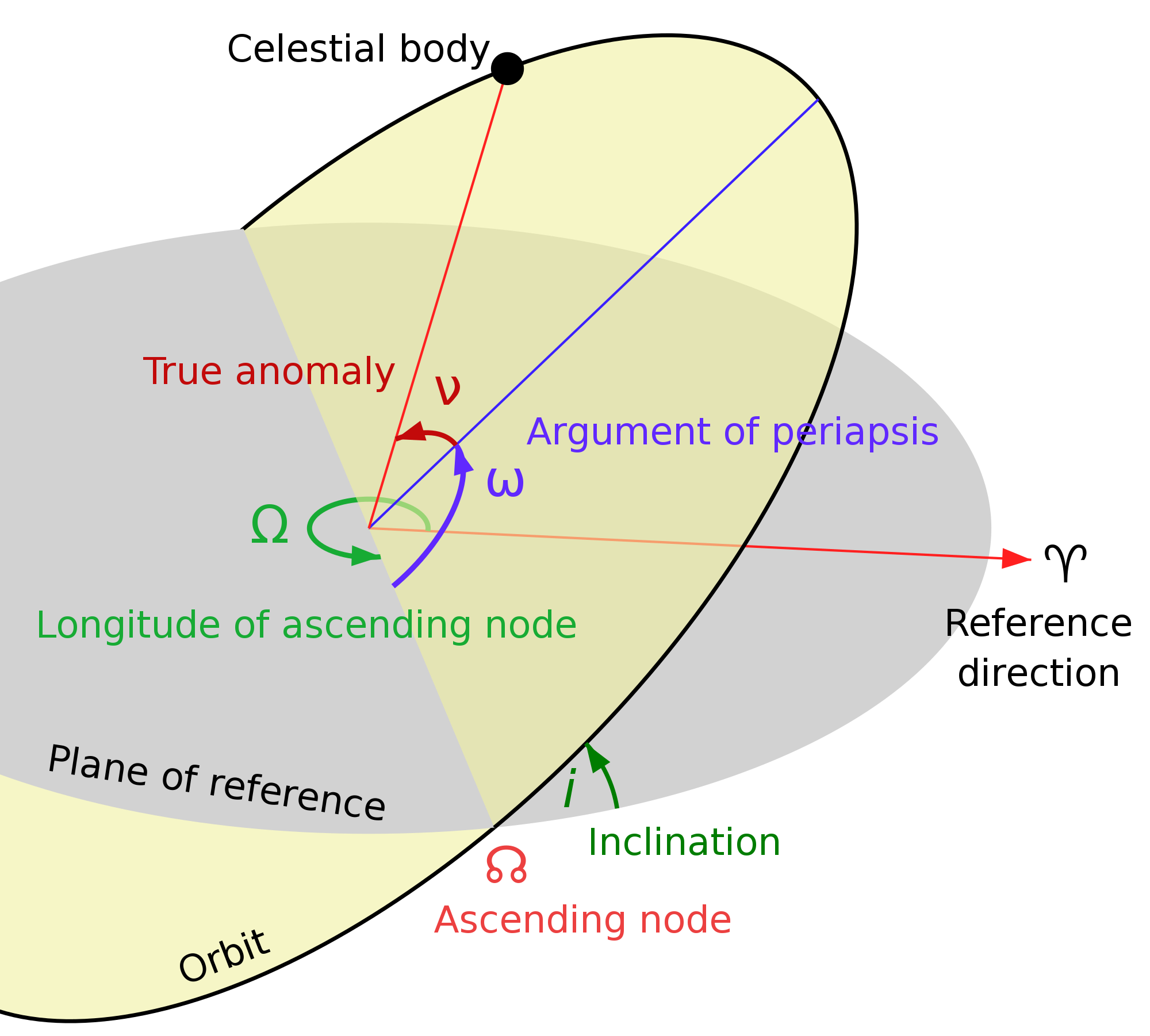
| || The origin elliptical Kepler orbit has four parameters we need to compute two $ \Delta V $ burns for our transfer orbit: <<BR>><<BR>> * Apogee $ r_a $ <<BR>><<BR>> * Perigee $ r_p $ <<BR>><<BR>> * Inclination $ i $ <<BR>><<BR>> * argument of perigee $ \omega $ <<BR>><<BR>>We can compute the semimajor axis $ a $ and the eccentricity $ e $ from the apogee and perigee <<BR>><<BR>>The angle of the ascending and descending nodes do not affect the $ \Delta V $ burns, though they do affect when we make our burns so we insert into the desired destination region of the M288 orbit.<<BR>><<BR>>|| {{http://upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Orbit1.svg/2000px-Orbit1.svg.png||width=300}} || | || {{http://upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Orbit1.svg/2000px-Orbit1.svg.png||width=300}} || The origin elliptical Kepler orbit has four parameters we need to compute two $ \Delta V $ burns for our transfer orbit: <<BR>><<BR>> * Apogee $ r_a $ <<BR>><<BR>> * Perigee $ r_p $ <<BR>><<BR>> * Inclination $ i $ <<BR>><<BR>> * argument of perigee $ \omega $ <<BR>><<BR>>We can compute the semimajor axis $ a $ and the eccentricity $ e $ from the apogee and perigee <<BR>><<BR>>The angle of the ascending and descending nodes do not affect the $ \Delta V $ burns, though they do affect when we make our burns so we insert into the desired destination region of the M288 orbit.<<BR>><<BR>>|| |
| Line 12: | Line 12: |
| || Blue curve:<<BR>><<BR>>An orbit in the horizontal X,Y plane<<BR>><<BR>>apogee = apoapsis = 6<<BR>>perigee= periapsis = 2<<BR>>semimajor axis = 4<<BR>>eccentricity = 0.5 || {{ attachment:orb01.png | |width=256 }} || || Red curve:<<BR>><<BR>>A similar orbit with a 45 degree '''argument of perigee''' <<BR>><<BR>>(rotate around vertical Z axis): || {{ attachment:orb02.png | |width=256 }} || || Green curve:<<BR>><<BR>>A similar orbit with a 30 degree '''inclination''' <<BR>><<BR>>(rotate around horizontal X axis):<<BR>><<BR>><<BR>>note that the ascending and descending nodes, where the orbit crosses the equatorial plane, do not have the same radius from the origin|| {{ attachment:orb04.png | |width=256 }} || |
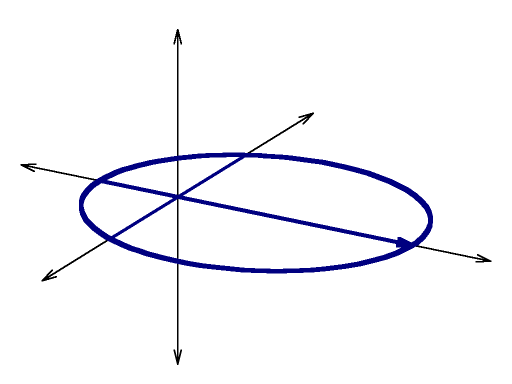
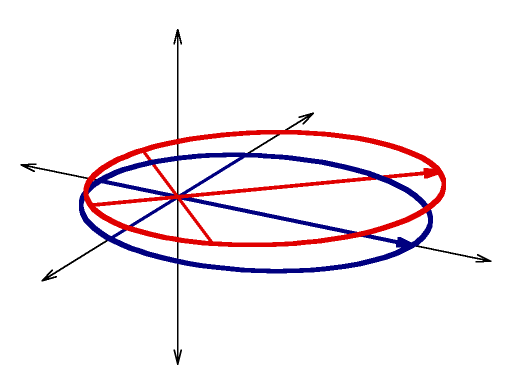
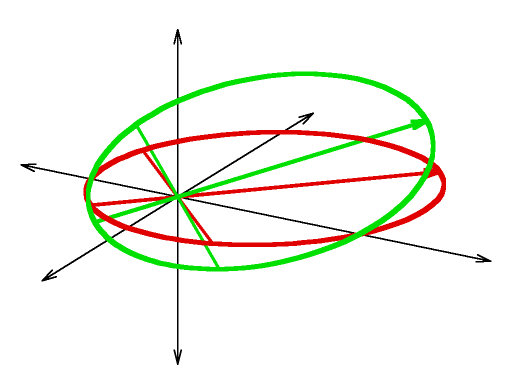
|| {{ attachment:orb01.png | |width=256 }} || Blue curve:<<BR>><<BR>>An orbit in the horizontal X,Y plane<<BR>><<BR>>apogee = apoapsis = 6<<BR>>perigee= periapsis = 2<<BR>>semimajor axis = 4<<BR>>eccentricity = 0.5 || || {{ attachment:orb02.png | |width=256 }} || Red curve:<<BR>><<BR>>A similar orbit with a 45 degree '''argument of perigee''' <<BR>><<BR>>(rotate around vertical Z axis): || || {{ attachment:orb04.png | |width=256 }} || Green curve:<<BR>><<BR>>A similar orbit with a 30 degree '''inclination''' <<BR>><<BR>>(rotate around horizontal X axis):<<BR>><<BR>><<BR>>note that the ascending and descending nodes, where the orbit crosses the equatorial plane, do not have the same radius from the origin|| |
Changing Orbits to M288
How do we get from any arbitrary orbit to M288? The following techniques may not be optimal for minimal \Delta V , but they set an upper bound. We will assume Kepler orbits and a circular M288 destination orbit, and heavy objects unaffected by light pressure. Actual thinsat orbits are elliptical and precess over a year with J2 and light pressure.
|
The origin elliptical Kepler orbit has four parameters we need to compute two \Delta V burns for our transfer orbit: |
Maneuvers use the least \Delta V farther out, so we will use different strategies depending on whether the apogee of the origin orbit is higher or lower than the M288 orbit r_288 .
Describing an arbitrary Kepler Orbit
|
Blue curve: |
|
Red curve: |
|
Green curve: |
gnuplot source and you will need to crop and convert and resize using gimp to reproduce the above images.
MORE LATER