Aerostat 183 GHz Rectenna for SSPS
This is a work in progress - many details to add and errors to correct
Space solar power satellites beaming 2.45 GHz or 5.8 GHz microwaves to earth require huge antennas and create enormous interference for communications, radar, and space science. We can make both transmit and receive antennas much smaller and cheaper, and eliminate interference to the Earth's surface, if we instead use 183 GHz ( λ = 1.64 mm ) and a 2 kilometer diameter aerostat rectenna at 20 kilometers altitude, feeding huge power cables to the ground.
Assume a rectenna at 60°N latitude, L = 40,000 km (4e7 m) from the rectenna. The first Airy null is 1.22 λ × L / RT kilometers from boresight where RT is the radius of the transmitter. If we make the rectenna radius RR a bit more than twice that, we will capture almost all of the transmitted energy, thus RT × RR = 2.5 λ × L = 410000 m2 . If RT = 410 meters, then RR = 1000 meters.
Assume an average receive power density of 1 kW/m2 (much higher at the center), for a total power of 3.2 GW. Assume that will be sent to the ground as differential 500 kV at 32 kA total.
Assume the aerostat platform is 100 meters high and filled with hydrogen. Since air density is 7% of the 1.225 kg/m3 at the surface, this platform displaces 0.086 kilograms per cubic meter, or 8.6 kilograms per square meter. The surface area is 3.14 square kilometers, so the total mass displaced is 27 million kilograms. Hydrogen has a molecular weight of 2, nitrogen a molecular weight of 28, oxygen 32, and ozone 48. Assume an average air molecular weight of 32, so the lift is 30/32 of the mass displaced, 25 million kilograms. If we assume 80% of the lift supports rectenna and multiwalled gasbags, this leaves 5 million kilograms of support to cables. This means cable weight (power and structural) can be perhaps 4 million kilograms, or 200 kilograms per meter to the ground. Assume 3 million kilograms consisting of 6 power cables, a matrix of 40% aluminum and 60% load-bearing Kevlar. So the aluminum cross section is 10 kilograms per meter, and the Kevlar is 15 kilograms per meter. The density of aluminum is 2700 kg/m3, and the density of kevlar is 1440 kg/m3, so the cross section of the solid material is 0.014 m2. Assume 3 times that volume, for electrical insulation. The diameter of a round composite cable is 23 centimeters, about 9 inches. The ground attach force per power cable is about 1.2 MN.
The 6 power cables will be caged in 6 smaller, uninsulated ground wires weighing 160,000 kg each, 8 kg/m, 6 kg/m of Kevlar jacketed in 2 kg/m of aluminum. The solid cross section is 0.005 m2, if round a diameter of 8 centimeters.
In both cases, the cables will not be round, but aerodynamic, teardrop cross section. The coefficient of drag is 0.04 for this shape; let's assume 0.2 with fluttering and ice buildup. Assume a drag cross section fror the big cable of 15 cm and the small cable of 5 cm, with drag coeeficient the effective drag area is 1.5 cm for the big cable and 0.25 cm for the small cable. Total drag area for six each of these cables is 10 cm.
|
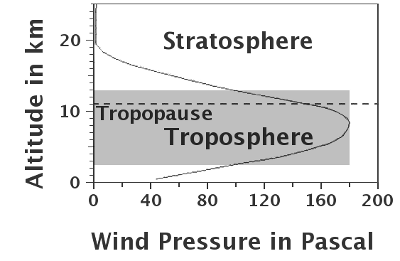
This is the wind pressure on the hanging power cables. Assume 11 km of 180 N/m2 wind force. 11000*0.1*180 = 200 kN; ratioed to the total ground attach force of 10 MN, that is an angle of 0.02 radians or 1.1°. Up to 10 km, that is a displacement of 200 meters |
Note: A platform at 60°N will be ellipsoidal, elongated 2.5x north to south to accomodate the 22° elevation of the geosynchronous source. So the lift force is 2.5 times, the cable mass and forces ditto. That will support a lot more wire cross section.
Lightning
Lightning is mitigated with grounded shield cables, surrounding the power wires in the middle. Each shield cable has an aluminum cross section of 7.4e-4, and the resistivity of aluminum is 2.8E-8 ohm-meters, so the resistance per meter is about 38 micro-ohms, or 38 milli-ohms per kilometer. The resistance from a 10 kilometer altitude is 0.38 ohms. A typical 20 kA lighting pulse will induce 7500 volts down the cable.
However, an absolute worst case 800 kA, 2 millisecond pulse will induce 300 KV down to the ground anchor (which should have a very low resistance bond to earth - this will be expensive!). 800kA in 38 μΩ produces a voltage drop of 30 volts, 800KA * 30V * 0.002s or 48 KJ of total energy dumped into 2 kilograms of aluminum, 24 J/g. The specific heat of aluminum is 0.9 J/g-K, so if the aluminum heated uniformly, it would heat by 27 K. In fact, because of skin effect it will probably heat a lot more on the outside for a few microseconds. Aluminum melts at 660C, so this gigantic lightning stroke might abrade a few millimeters of outer aluminum.
Hydrogen and Aerostat Scale
The numbers above are for a gigantic aerostat platform, with a volume of 300 million cubic meters. For comparison, the Hindenburg airship contained 200 thousand cubic meters. However, this aerostat does not need to power itself through the air, and will rarely have staff aboard. The large volume can support multiple layers of puncture protection, perhaps with CO2 or argon in the interstitial spaces. The aerostat itself will need lightning protection; it is a smaller object than the cables to the ground, and it can be caged in more shield wires attached with high voltage insulators and connected to the grounding network.
Both the hydrogen inside the gas bag, and the oxygen outside, will be very cold, and at 0.07 atmospheres. This will hinder combustion should the two mix. However, for proper protection of the ozone later, they should be very well separated, and high voltages (and potential arcing) should be shielded from the gas bag.
This will not be simple or cheap, but it will be a lot cheaper and environmentally safer than 50 square kilometers of lower frequency surface rectenna.
Smaller Scale, Lower Efficiency Alternatives
The first SBSP systems should be smaller and less efficient so they are easier to test. If they are launched by and used to power mid-ocean Launch Loops, then the most important goal is to add power and launch capacity for the Launch Loop and expand the system quickly, so that it may spread rapidly into new global markets before competing with established markets. 50% capture occurs at half of the Airy ring, or R_R R_T = 0.6 D /lamda ≈ 66000 m²
Assume the transmitter produces (on average) 0.75 of peak power, a simple flat-to-tilted disk with transmit power P_AT = 200 W/m². Assume the receiver power can be as high as P_AR ≤ 1000 W/m² in the cold stratosphere, at 80% efficiency. If the total power P = 0.3 \pi P_AT {R_T}^2 = \pi P_AR {R_R}^2 , we can estimate the minimum sized system as a transmitter 500 meters radius and a rectenna of 140 meters radius, with an average receive power of perhaps 45 MW. The transmitter peak of 200 W/m² might require a structure of 10 kg/kW or 2 kg/m², or 1600 tonnes.