|
Size: 1405
Comment:
|
Size: 1736
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 5: | Line 5: |
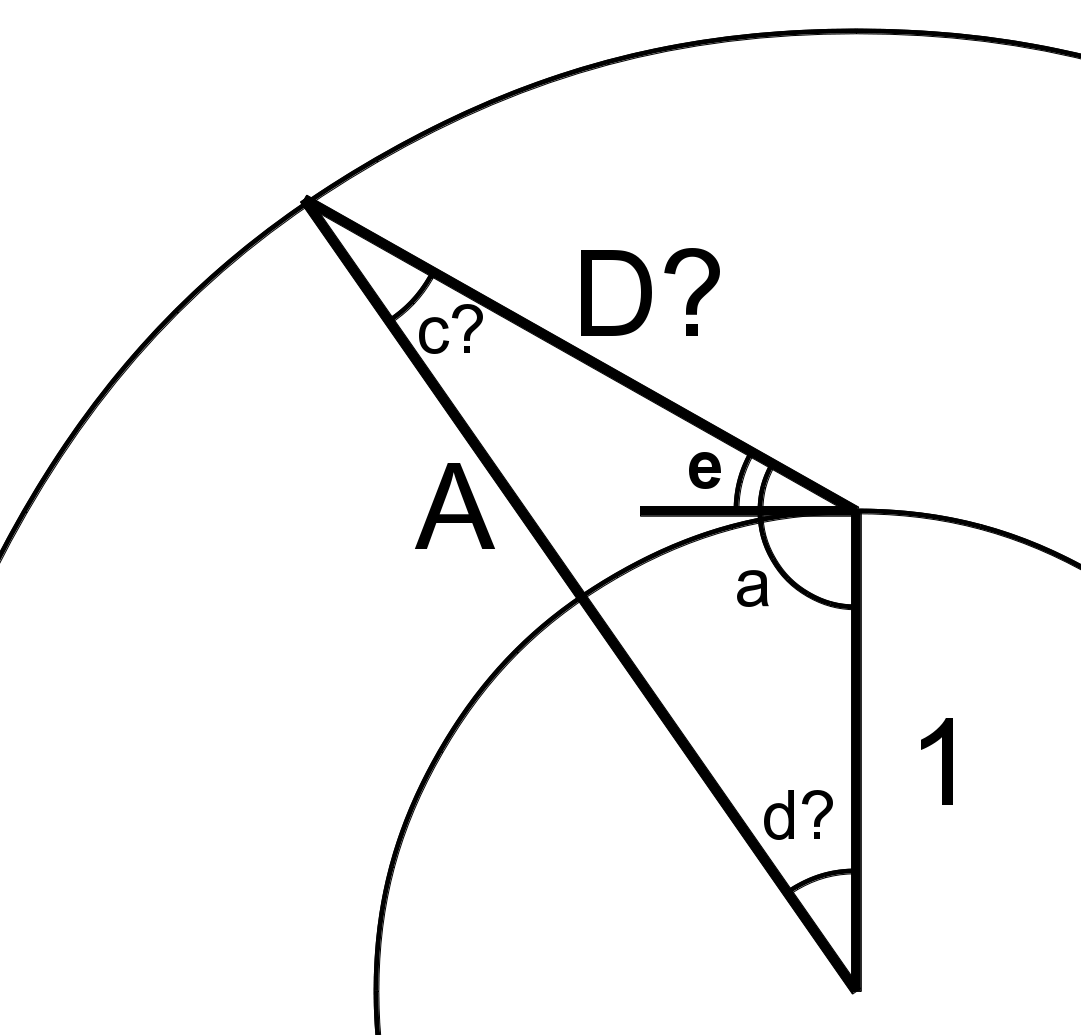
| || Thinsat arrays will not always be directly above the ground antenna, but will be at an elevation angle $ e $ above the horizon. If the array orbits at a radius $ A \bullet R_E $, what is the distance $ D \bullet R_E $ between the array and the ground antenna? Note that $ D = 1 $ when elevation angle $ e $ is $ \pi / 2 $ or 90°. || {{ attachment:SatDistance.png | | width=200 }} || | || Thinsat arrays will not always be directly above the ground antenna, but will be at an elevation angle $ e $ above the horizon. If the array orbits at a radius $ A \bullet R_E $, what is the distance $ D \bullet R_E $ between the array and the ground antenna? Note that $ D = 1 $ when elevation angle $ e $ is $ \pi / 2 $ or 90°.<<BR>><<BR>>Signals between satellite and ground are attenuated by distance, though at 70 GHz attenuation due a longer slant path through the atmosphere is more important. For the M288 orbit, where A ≈ 2, $ D = \sqrt{ 3 } if $ e = 0 $, attenuating signals by 10 log 3 or 4.8 dB. The atmospheric attenuation is far greater. || {{ attachment:SatDistance.png | | width=200 }} || |
Satellite Distance
Thinsat arrays will not always be directly above the ground antenna, but will be at an elevation angle |
|
The sin law states that:
{ { sin( d ) } \over D } = { { sin( a ) } \over A } = { { sin( c ) } \over 1 }
sin( a ) = sin( e + { \pi \over 2 } ) = \cos( e )
sin( c ) = { { sin( a ) } \over A } = { { cos( e ) } \over A }
cos( c ) = \sqrt{ 1 - \left( { cos( e )^2 } \over A \right)^2 }
The sum of the corners of a triangle is \pi , so
\pi = a + c + d = e + { \pi \over 2 } + c + d \;\;\;\;\;\;\;\;\; { \pi \over 2 } = e + c + d \;\;\;\;\;\;\;\;\; d = { \pi \over 2 } - ( e + c )
sin( d ) = sin( { \pi \over 2 } - ( e + c ) ) \;\;\; = cos( e + c ) \;\;\; = cos( e ) cos( c ) - sin( e ) sin( c )
D = sin( d ) / sin( c ) \;\;\; = cos( e ) cos( c ) / ( cos( e ) / A ) - sin( e ) sin( c ) / sin( c ) \;\;\; = A cos( c ) - sin( e )
D = A \sqrt{ 1 - \left( { cos( e )^2 } \over A \right)^2 } - sin( e ) \;\;\; = \sqrt{ A^2 - cos( e )^2 } - sin( e )
D = \sqrt{ ( A^2 - 1 ) + sin( e )^2 } - sin( e ) |