Solar Cell
The following is for a silicon solar cell substrate - the likely product of a lunar factory. Earth-launched solar cells will be Indium Phosphide on aluminum.
The thickness of the thinsat, and its weight, and the cost of launching it, is determined by the thickness of the solar cell. Most mono-crystalline solar cells are thicker than 150 microns, but 65 micron thick cells have been reported. How thin can a cell get?
100 micron thickness may be needed for safe mechanical handling in production, and to minimize curling. Ultrathin solar cells ( a micron or less ) will be optically translucent, and will not absorb very much sunlight. How thick does a cell have to be?
Light absorbed in solar cell silicon generates hole-electron pairs. For a P- solar cell with an N+ top junction, electrons drift towards the top junction, are accelerated across the depletion region, and collect on the N+ cathode, where they are collected and run through the external circuit. The holes drift to the bottom electrode, which is also a mirror, doubling the optical path. Photons that pass through the silicon in both directions are not captured, which can happen if the cell is too thin, or if the photon energy is too small to make carrier pairs.
Fortunately, the absorption is rather good above 1.2 eV, meaning that most shorter wavelength light is captured, even for thin silicon. Very thin single-crystal solar cells are still relatively efficient.
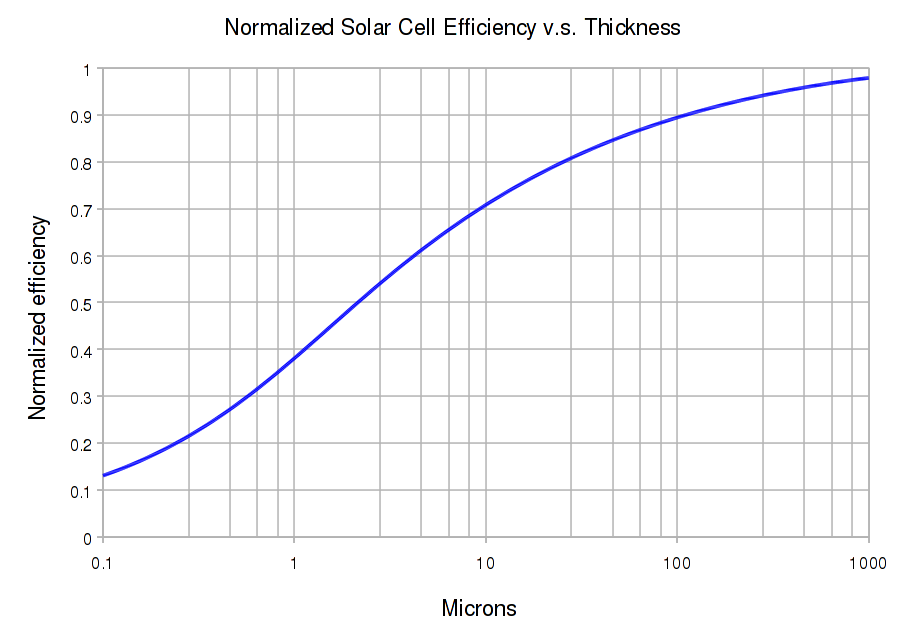
This graph estimates the efficiency of the solar cell as it gets thinner. While efficiency goes down with thickness, the efficiency per thickness and weight is best for very thin cells. |
|
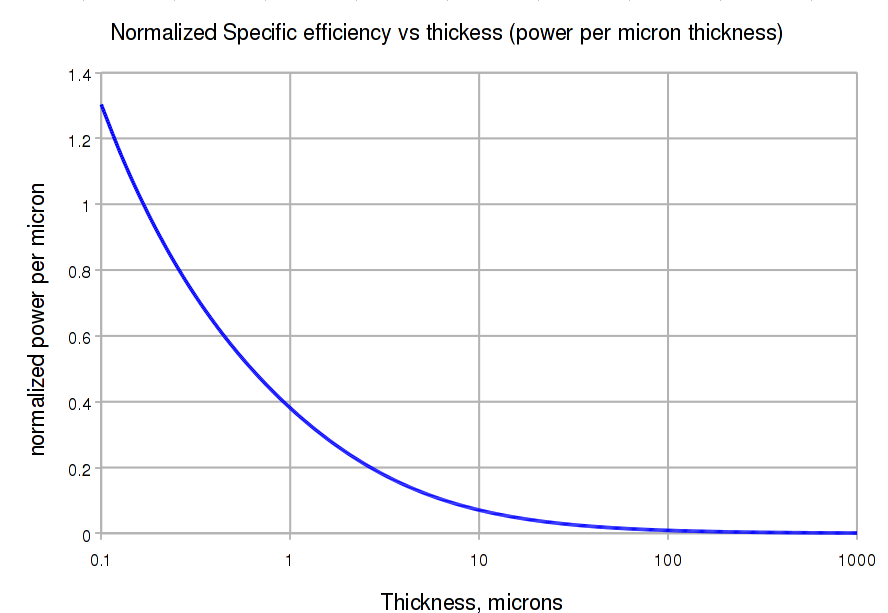
This graph estimates the efficiency per thickness, as above. Though a 0.1 micron thick solar cell is not an efficient collector of sunlight, the power per weight is very high. If a 150mm cell captures 5W at 100 micron thickness (about 700W/kg), it will capture 650mW at 0.1 micron thickess (90kW/kg). Backside wiring and electronics will probably not shrink much below 2 microns or so. |
|
The above graphs are based on the optical properties of silicon from the Virginia Semiconductor website, and this solar power spectrum. I am assuming one hole-electron pair per absorbed photon, regardless of energy, and derate the power flux at high photon energies proportionally to photon energy. Photons with less energy than the bandgap don't get absorbed, and hence contribute no power.
If there are better estimates in the literature for the efficiency of thin mono-crystalline silicon solar cells, I would love to hear about them.