SSPS Interference with Airport Radar
ARSR-4: Air Route Surveillance Phased array Radar
ASR-11: Airport Surveillance Radar, Terminal Area
( AN/GPN-30 )
PSR Probability of Detection: The PSR shall be capable of detecting a 1.0 m2 Radar Cross Section (RCS), Swerling 1 target to a range of 55 nmi in the clear and at the nose of the beam with a single scan Pd of 0.8 and a Probability of False Alann (PFA) of 10-6 •
Operational Subclutter Visibility: Operational SCV shall be 42 dB minimum at all ranges for nonfluctuating targets.
|
ARSR-4 |
ASR-11 |
|
Band |
L Band |
S Band |
|
Peak Power |
60 kW |
25 kW |
|
Average Power |
|
2.1 kW |
|
Wavelength cm |
21.4-24.7 |
10.3-11.1 |
|
Frequency GHz |
1.21-1.39 |
2.7-2.9 |
|
Max interference |
? |
-117 |
dBm/MHz!! assumed EIRP |
LNA bandwidth |
? |
? |
|
IF bandwidth |
? |
1 MHz |
Table D2 pg 107 13-490 |
Polarization |
Linear |
Linear |
|
|
Circular |
Circular |
|
Beam width |
1.41° |
1.41° |
|
Beam Elevation |
2.2° |
4.8° |
|
Antenna Gain |
|
34dB |
|
Antenna Size |
9 x 7 m |
5 x 3 m |
|
Pulse width |
|
1μs |
|
|
|
80μs |
|
Coverage nm |
250 nm |
60 nm |
|
Coverage km |
463 km |
111 km |
|
Scan period |
12 sec |
12 sec |
|
Weather map |
36 sec |
|
|
# deployed |
43 |
213 |
13-490 Effects of Wimax on airport radar and weather radar.
Guessing about radar
If we presume the beam energy is confined to an area of 6.77 square degrees out of a 41253 square degree sphere, that would be a gain of 37.85 dB. Since the specified gain is 34 dB, more power ends up in sidelobes than presumed.
If the antenna gain is 34 dB, and the peak pulse power is 25 kW, that suggests that the EIRP is 63 MW. A 1 m2 target at a range of 111 km gets 400 microwatts of illumination. If that radiates back with a 1 steradian spread, it delivers 83 pW to the antenna, -70 dBm (?).
|
Sidelobe graph, Cleaned up from Arndt 1978 |
|
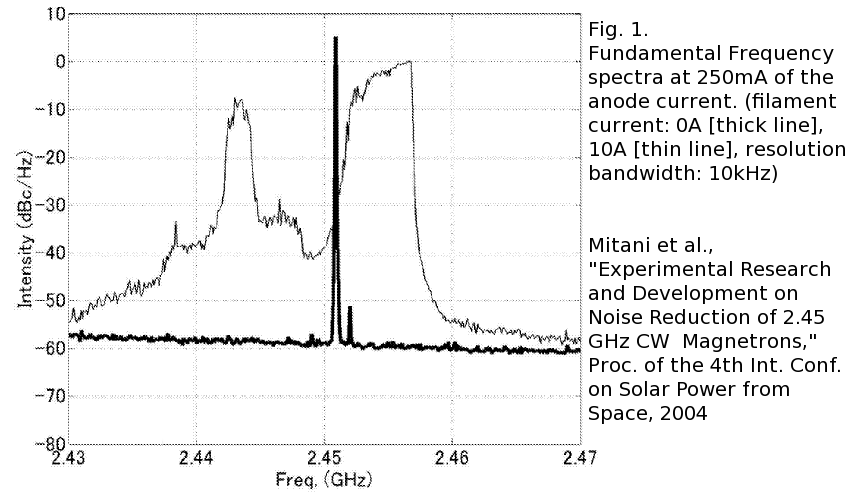
This is the noise from a magnetron. Not sure how to interpret this - if we assume a 1 MHz bandwidth and extrapolate to -70 dBc/Hz at 2.7 GHz, how much noise power is that assuming a 15 mW carrier hitting the 5x3 meter antenna? |
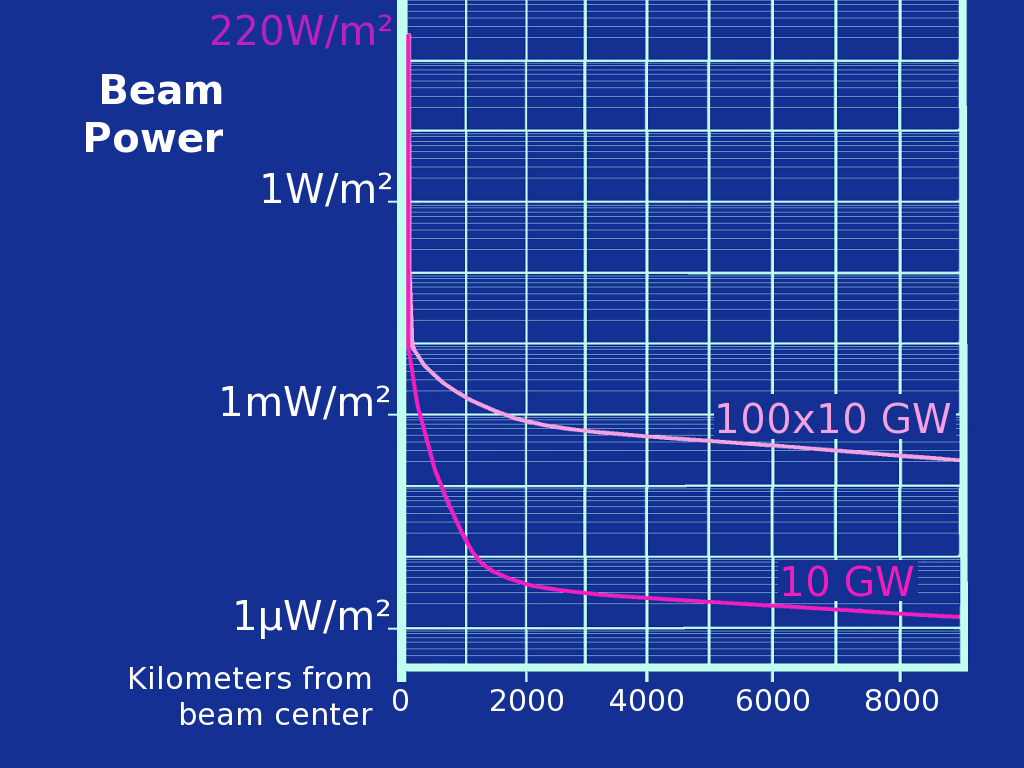
Of course, the SSPS (Space Solar Power Satellite) is not pointed at a radar, but it does create 100's of megawatts of sidelobe power lighting up the whole earth. The radar dish does not point at SSPS overhead, but if there are 100 in orbit, some will be near the horizon within the 360 degree antenna horizontal and 40 degree vertical scan. A radar will see any SSPS that appears near the horizon, and at low elevation there will be significant atmospheric and terrain scattering.
Pulsed SBSP as Bistatic Radar Illumination Source
If you can't fix it, feature it. What if we used the SBSP beam as the source of radar illumination power?
SBSP (Space Based Solar Power) efficiency is limited by the rectifying diode drop; a Schottky diode requires perhaps 0.5V to turn on, which is subtracted from the peak dipole voltage. For a given average rectenna power density, say 250 W/m², the peak voltage field is √2PR, where R is the 377 Ω/□ impedance of free space, or 434 V/m. For a 2.45 GHz beam, a dipole antenna is 6.1 cm, so the peak dipole voltage is 26.4 volts, unloaded. My guess is that with a matched load, this is cut in half, to 13.2 volts. The diode drop uses 4% of the power.
If we deliver the same average power as high power, low duty-cycle pulses, the voltage increases by the inverse square root of the duty cycle. The ASR-11 has a duty cycle of (2.1/25) or 8.4%, with a pulse width ranging from 1 μs to 80 μs, implying a period of 12 μs to 1 ms. Let's drive the SSPS the same way. That increases peak power by 1/0.084 to 3000W/m², and the matched dipole voltage to 46 volts. The diode uses only 1% of the power (unless I²R resistive losses are increased).
That is helpful, but the main advantages of pulsed SSPS power are:
- 1) With 8% pulses, 92% of the time period becomes available for other uses, like communications and radio astronomy.
- 2) Higher peak voltage fields permit shorter wavelength power beams, and smaller rectennas and transmitters.
- 3) Multiple beams from different SSPS satellite sources can be combined at one rectenna, without interference effects.
- 4) The pulse can be the source of bistatic radar illumination energy, greatly improving radar operation.
Let's concentrate on advantage #4, because it transforms enemies into allies; SBSP can become an integral part of next-generation aircraft radar, increasing public safety. It also transforms small scale prototype power satellites into useful sources of radar energy, not mere experimental platforms. This can be a profitable path to SBSP, the missing link between existing 25 kW comsats and future 2.5 GW space power systems.
A bistatic radar separates the transmitter from the receiver. If both are on the ground, it can be difficult to synchronize transmitter and receiver. The system is still subject to the 1/R⁴ problem, both transmission and reception are attenuated by 1/R² . The intensity of the transmit beam can be a health safety and interference problem near the transmitter.
But what if the beam is sourced from a powerful satellite transmitter in the sky, illuminating the entire region around the receive antenna? A GEO satellite will need high antenna gain to illiminate "only" a 111 km radius patch on the ground, 40,000 km away, but the gain can be much lower than that required for an SBSP rectenna, and the space antenna much smaller.
The radius of the transmit antenna times the radius of the illuminated area is proportional to the wavelength times the distance. For a 0.12 m wavelength at a 4e7 m distance, the product is ≈5e6 m². For a ground radius of 111 km, the transmitter radius is approximately 50 meters; large compared to a comsat, but 1% of the area of a 1 km diameter SBSP antenna (which presumes a 5 km radius rectenna).
Illuminating that entire area with a pulsed power density of 400 W/km² (average 34 W/km²) wastes power: 1.3 MW average versus 2.1 kW. However, by eliminating the transmitter, the receivers can be cheaper and more numerous. If they are more closely spaced, the returns from a closer object will be higher power, or we can use smaller antennas. If more than one antenna is observing an object, we can use time of flight and trigonometry, not antenna pointing and azimuthal selectivity, to determine object location.
If the transmitter solar array size is proportional to a 50 meter radius antenna size, the collection area is 7850 m². If that is 15% efficient PV in 1360 W/m² sunlight, the DC power production is 1.6 MW, sufficient to produce (somewhat inefficiently) 1.3 MW of microwaves.