Switched Three Phase Slot Antenna Drive
Note, 2015 April 21: This will not work without modification. Different frequencies will scatter at different angles. With a signal bandwidth of 1 GHz, and a thinsat 20 cm wide, and a beam angle of 45°, there is a ±234 psec difference at the edges of the array, ±0.117 radians at 500 MHz, ±6.7° of aiming error for the "edge" frequency components. If we can add a frequency-dependent phase component for each antenna, as well as feed from multiple locations with skewed phase for each data channel, perhaps this can be fixed.
A server sky array produces a few watts of transmit power, divided by more than 10 million antenna slots on all the thinsats. That means less than a microwatt per antenna slot - even with 3KΩ slot impedance, that is less than 100mV peak to peak, which is difficult to make efficiently from a 1 volt power rail. Digitally synthesizing a thinsat's broadcast signal at every die is also power-hungry.
Instead, imagine that many chips on a thinsat have synthesis and amplification capability, but only a few are turned on, driving a net of three phase 70 GHz signal rails feeding all 350 chips. Every chip is hooked up to those three rails, and has a three way selector switch between 0°, 120°, and 240° phased versions of the broadcast signal. The switched signal is fed (perhaps through a capacitor) to the antenna slot.
Ideally, each slot would be phased exactly for the signal it is supposed to transmit, given the angle and relative distance to the distant target, computing the "reciprocal wave vector". If the actual phase deviates from the ideal by angle θ, there will be a cos2(θ) loss of contribution to the power reaching the target, the rest of the power will be scattered off-target. But our targets are individual square-meter receivers, so all of the power not reaching the target is wasted anyway. Feeding an antenna slot with out-of-phase power is a win if it saves system power, and averages out to a useful broadcast beam.
In detail, the center-of-beam power is the square of the sum of the voltage (or current) amplitudes of all the slots in the array. The in-phase amplitude is cos(θ) and the average in phase amplitude is:
{average} = { \Large { 1 \over {\theta} } {\int_0}^{\theta} } \cos({\theta}) d{\theta}
{average} = { \Large { { \sin({\theta}) } \over {\theta} } }
The array power is proportional to the square of that average, so
{power}~{efficiency} = { \Large { \left( { \sin({\theta}) } \over {\theta} \right)^2} }
For a 3 phase system, θ is π/3 (half of the total angular "sweep" of 120°). Here's the average amplitudes and efficiencies for various numbers of phases:
phases |
Sweep |
theta (radians) |
mean amplitude |
power efficiency |
sidelobes |
3 |
120° |
π/3 |
0.827 |
0.683 |
-3.3 dB |
4 |
90° |
π/4 |
0.900 |
0.810 |
-6.3 dB |
5 |
72° |
π/5 |
0.935 |
0.875 |
-8.5 dB |
6 |
60° |
π/6 |
0.955 |
0.912 |
-10.2 dB |
The sidelobes in the table above are not the total sidelobes, just the additional sidelobe energy due to the slot selection scheme. Far more sidelobe energy will result because the array is sparse, though this per-thinsat sidelobe energy will spread some sidelobe energy beyond the 20 milliradian (200 km) main Airy disk central lobe associated with thinsat size.
|
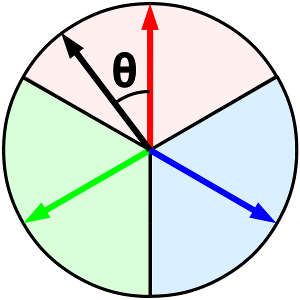
Illustrating the selection of one of 3 phases per antenna slot. The black arrow represents the ideal phased signal to be emitted from the antenna slot - it is within the 120 "red" sweep, so the red vector is chosen by switches on the chip driving that slot. The usable power is the vector dot product of the two arrows, the cosine of the angle θ, and the waste power is the difference between the square of the vectors. Averaged over the sweep, the power efficiency is 68%. The loss power will create some sidelobe interference, but the power is spread over all of space, tiny compared to the 60 pico-steradian concentrated beam sent to the intended target receiver. |
Assuming 380 μW per thinsat transmitted, the difference in power loss between three phases and six phases is 141 microwatts; it will cost far more than that to distribute three more phases around the thinsat.
At a gigabit per second, a 9000 byte jumbo frame requires 72 microseconds to transmit; during that interval, the array (orbiting at 4650 m/s) moves 33.4 centimeters. With a 300 meter diameter ground spot (to -3dB), we could transmit 900 frames with the same phasing before recalculation, every 65 milliseconds (about a ping time). Practically, we can recompute phase every 10 milliseconds per slot and stay within 0.1 dB of optimum.
The 100 meter diameter array rotates every orbit, and thinsats move as fast as 2 cm/second north/south while it does so. Over the same 10 milliseconds, the thinsats change their position (and hence phasing) by 0.36 mm - this is a significant fraction of the 4.3 mm wavelength, but it is "common mode" to the whole thinsat. We can take care of this doppler-like movement by adjusting the phase of the common signal rails by 30° over the course of the movement, rather than re-selecting the slot feeds. That common mode phase adjustment will depend on the dot product of the azimuth vector of the target and relative velocity vector of the thinsat to the array. If a multiplexed array is simultaneously sending to multiple ground targets using multiple bus groups, each three phase bus must be adjusted separately for each dot product.
Computing a two bit value (three phases or off) for 1400 slots per thinsat 100 times per second is a really cheap calculation. Even if radiation hits upset the calculation or the bit settings for one slot selector, the "sparkle noise" will not reduce main beam amplitude noticably for a whole array. Of course, the calculation must include the position of each antenna and the current shape of the (possibly vibrating) thinsat, the precise direction of the target (within a microradian), temperature, switch resistance and voltage, and many other complications, but this is just another application of the transistor hose.
Summing two vectors
Look at the phase circle. The sum of two vectors produces another on the black line between them, and results in a six phase system. If the summing is efficient (say through a pair of capacitors, while maintaining the impedance to the phase buses) then our power efficiency goes up, and sidelobes drop by 7 dB.
As part of the 100 Hz rate configuration cycle, we will configure and balance the RF buses. These will be driven from multiple points and have stubs, some of them terminating on buses interrupted by micrometeoroid punchthroughs or dead chips. The parameters used to select and calibrate the drivers feeding the buses will be precomputed and stored in EPROM, and recomputed every time some unpredictable accident damages the network, and also during slack operation times.