Gossamer Torque Radiator for SSPS
Server sky will produce data worth far more per space megawatt-hour than grid electricity, but after a terawatt of global data service is generating $40T per year of net profits(1), those profits, plus the launch and deployment infrastructure developed for server sky, can lead to additional revenue from space solar power delivered to Earth as "dumb" energy. 50 Terawatts of electricity at $20/MWh is a gross revenue of only $10T per year (and profits are likely to be negative). However, cheap clean grid electricity can power more data-enabled terrestrial applications, increasing data demand and supporting further server sky system growth. Sell the data services, and give away the power below generation cost to enable the consumption of more data services.
So, it makes sense to think about gossamer technology techniques for generating "dumb" space power. Transmitting space power as microwaves to Earth is very very difficult. Due to diffraction limits, the transmitters and receivers must be enormous, square kilometer scale as opposed to the square-decimeter scales of server-sky thinsats. Because of the "sparse array curse", the power transmitters must operate as huge, physically continuous systems, which subjects them to tidal forces that cannot be corrected with light pressure. We must rely on physical strength of materials, and correction torques, though we can still be clever about how to use those materials in a gossamer way.
The radiator problem
Some proposals for the power plants (which power the microwave generators) are photovoltaic surfaces, others propose heat engines. The problem with heat engines is that they must radiate the waste heat with black body radiation, and radiating that heat at a low temperature requires a very large surface. Most proposals assume radiating fluid (liquid or gas) coolant in sealed pipes and channels. There are many problems with this:
- The channels can freeze during eclipses at the equinoxes; as the orbit passes into the shadow behind the Earth, up to 70 minutes of darkness and cold. Not complete 2.7K deep space cold; the Earth radiates infrared heat at 250K, and attenuated by distance, that will warm a flat radiator facing Earth to about 100K. Still, that is certainly cold enough to freeze any working fluid with a decent specific heat that is liquid or gas at heat-turbine working temperatures. A lightweight radiator will have very small thermal mass as well, and will plummet towards 100K quickly.
- Sealing plumbing against micro-meteoroid damage will also be difficult.
- Fluid radiators suffer from scaling issues; transmitting heat twice as far across a radiator requires twice as much fluid in transit. The amount of fluid scales as the square of the radiator surface. The amount of power wasted pumping it around goes up, too; it has farther to go, and more wall viscosity to push past.
The torque problem
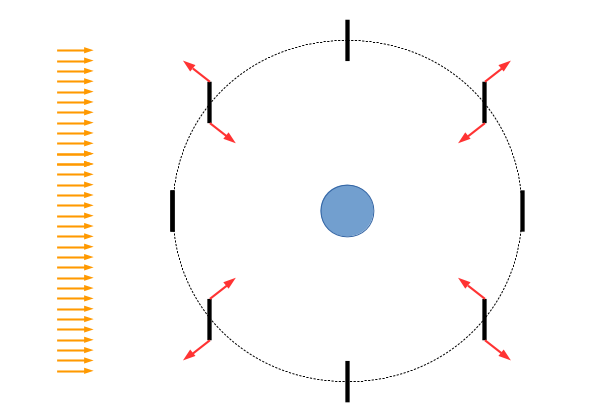
SSPS systems suffer from another big problem - they must keep their solar collection systems (PV or mirrors) pointed at the Sun, following it as it seems to rotate around an axis perpendicular to the orbit direction and the tidal vector towards the Earth. The panels will be tilted around that perpendicular axis, which means they will generate torques along that axis, too. Holding them steady (as opposed to oscillating back and forth perhaps 20 degrees over a 24 hour period) requires added torque.
Stringing the system vertically, and adding a "kite tail" mass towards earth, seems like a solution; unfortunately, this system will be end-on towards the Sun near noon and midnight, and unless the collectors stick out in different directions, they will shade each other.
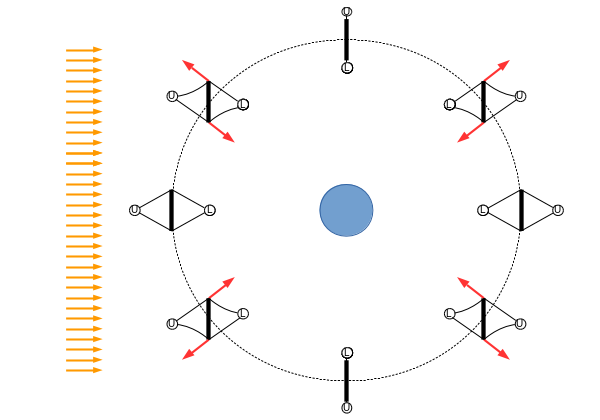
A possible solution is shown in the figure on the right - hanging counterweights. The counterweights shown here are very close to the SSPS, as shown they must mass half as much as the SSPS itself to counteract the torque. If they are spaced many system widths up and down, their masses can be reduced proportionally. For a 2 kilometer wide SSPS, counterweights deployed 100 km up and down might mass on the order of 1% of the SSPS mass. Much depends on how the mass of the SSPS is distributed, whether the masses are on the end of an extended spar to increase leverage, etc.
For the system shown, there is a troublesome topological problem; at the 6AM/6PM terminator position, the counterweight cables must swap positions, front to back, or the counterweights attached to them must swap end to end. For a two dimensional surface, there must actually be four connections (also at the corners to maintain stability in two axes). In addition, a cable can be sliced by an impactor, and a counterweight could be lost, crippling the SSPS. Recovery systems would be needed for stray counterweights, also pieces falling off the SSPS itself. The devil is in the details - handwaving and vagueness won't protect multibillion dollar assets.
For many satellites, the solution is "momentum wheels" - heavy flywheels on bearings inside boxes. Flywheels have maximum rim speeds, proportional to the square root of the material strength divided by the density, on the order of 1000 meters per second for strong materials like Kevlar. The angular momentum (torque multiplied by time) is proportional to the rim speed times the rim mass times the radius. Storing a lot of angular momentum in a limited size satellite box (restricting wheel radius) requires a lot of mass, and the high RPMs make bearings fail. The Kepler space observatory was crippled when its momentum wheels failed.
Torque radiators
Let's abandon two crippling assumptions:
- 1 The torque wheels must stay in the box. WRONG.
We have trillions of cubic kilometers of empty vacuum to deploy into.
- 2 The radiator must distribute the heat in fluid. WRONG.
We can move heat in solids, which do not evaporate in vacuum, and do not leak when punctured by a micrometeorite.
The specific heat of water is 4.2 J/g-°C, and the phase change properties can move a lot of energy. The specific heat of Kevlar is only 1.4 J/g-°C, but it "remains Kevlar" over a much wider range of temperatures. More importantly, Kevlar can move a lot faster than water can, with zero friction in vacuum. A "nozzle" emitting a wide gossamer ribbon of heated Kevlar into space can move a LOT of heat. If the Kevlar surface is designed for high infrared emissivity (an electrical sheet resistance of "spacecloth", 377 Ω/□) it can radiate the heat very fast. Indeed, if the "spacecloth" is designed to be absorbant in the infrared band, and reflective in optical light, it can be an effective infrared heat emitter at 10 μm wavelengths (Wein peak at 300K) and below, and reflective at 1 μm wavelengths and above (most of the solar spectrum). Assume that this magic ribbon is 80% thermally emissive and 20% absorptive of the solar spectrum, flat to the sun.
A big loop of Kevlar strengthened film can be shot out into space, where it radiates and cools, then is pulled back into the working core by adaptive rollers. The speed of sound in Kevlar is around 7000 meters per second, so tension waves propagate far faster than the 1000 meter per second band can move. Practically speaking, the rollers can't move nearly that fast. Assume a design speed of 400 m/s, with longitudinal high strength Kevlar "tracks" separated by lateral pleats for curl resistance. With good modelling and a series of fast actuators, a Kevlar ribbon can be positioned and oriented to feed back into the rollers for another cooling pass. After all, it only moves only 40 millimeters in 100 microseconds, the time it takes for a measurement laser beam to move 15 kilometers out and back.
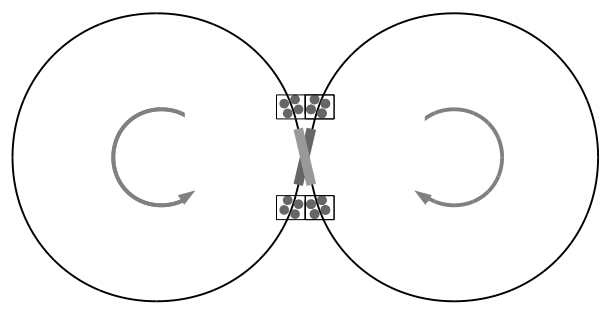
Two counter-rotating loops of Kevlar radiator will have zero net angular momentum (that is, torque storage), and may spread out over many kilometers. The ribbon is "out of control" in the loop; it will probably turn and twist relative to the Sun, so the radiative surface will average 50% area oriented to the Sun, while 2 times the area will radiate into space. Absorbing on average 137 watts per square meter from the Sun, and radiating that with an emissivity of 0.8 on both sides results in an equilibrium black body temperature of 210 Kelvin.
Kevlar retains strength above 150 °C, or 420 K, so both sides of an 80% emissive ribbon can radiate 2200 W/m² at 420K. Two circles of Kevlar ribbon ten meters across and 2 km in diameter could emit perhaps 100 MW. Kevlar has a heat capacity of 1400 J/kg-K. If a 400 m/s ribbon weighed 2 kg/m, it would have enough heat capacity to carry away 100 MW with a temperature difference of 100K. Total mass of a loop, 13 metric tonnes, 130 g/kW.
Two loops might look like this - the actual roller system and heat exchanger would look different. The rollers could be magnetically suspended, with an internal multiblade fin arrangement to move heat from an inner radiator. However, it may be possible to build the entire heat turbine into the roller, and use gas dynamics and roller position relative to sunlight and cooling loop to create the turbine "cycle". I'll leave that to a clever aerodynamicist to figure out.
The density of Kevlar is 1400 kg/m³, so a 0.2 kg/m² ribbon might be 300μm thick. The thermal conductivity of Kevlar is poor; 0.04 W/m-K. The "characteristic time" of a ribbon heated from one side is the thickness squared times the heat capacity per cubic meter, divided by the thermal conductivity. The heat capacity per cubic meter the heat capacity per kilogram times the density, 1400 J/kg-K times 1400 kg/m³, or about 2e6 J/K-m³. So, t = (3e-4 m)² × 2e6 J/K-m³ / 0.04 J/s-m-K = 4.5 seconds.
Obviously, the thermal conductivity must be improved. Aluminum has a thermal conductivity of 240 J/s-m-K; if the ribbon is 10% aluminum (perhaps in the non-load-bearing crossribs), with 30% effective thermal conduction paths, the composite thermal conductivity increases from 0.04 to 7.2 J/s-m-K, and the characteristic time drops to 25 milliseconds, 10 meters of movement.
Imagine that the ribbon is wrapped 180 degrees around a 20 meter diameter roller, with an effective contact length of 60 meters; that provides a 150 millisecond contact time. The "wetting" of the roller to the aluminum may be poor, so even more contact time may be needed, perhaps multiple rollers or a transfer band that makes contact for a considerable length longer than one roller.
Again, it may be possible to build the turbine inside the roller itself, a hollow surface system made up of many small cells. Inside the turbine roller could be a distributed magnet surface acting on fixed coils, generating high frequency AC into a multiphase high-speed-diode rectifier, directly feeding solid state microwave generators broadcasting into a large bore (tens of meters) dielectric waveguide, feeding down to the broadcast antenna.
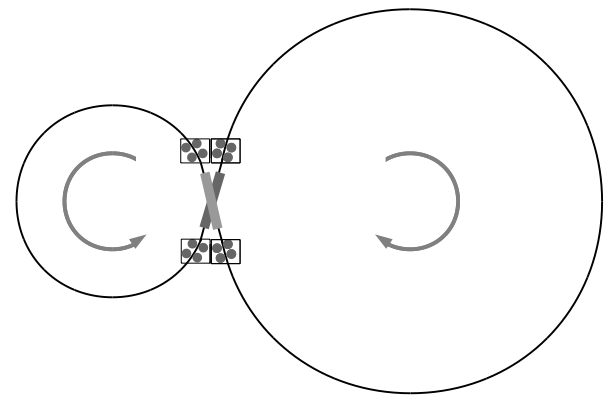
But what about torque adjustment? The structure as shown "stores" equal but opposite amounts of torque. How to generate a net torque clockwise or counter-clockwise? Simple. Temporarily pull more from the left loop, and pull less from the right loop, and the right loop will grow, as shown:
This will shift the system center of mass; two pairs of loops rotating in opposite directions could shift loops in opposite directions, providing the differential torque storage without moving the system center of mass. The torque transfer will not be fast; a large shift left to right might take 30 thousand seconds, more than 8 hours, a thousand rotary cycles.
These systems will be complex to design, but could be gossamer thin. It costs nothing to launch clever money-saving engineering. Space systems have three important degrees of freedom not found on Earth: weightlessness, vacuum, and infinite space. Space engineering (with robotic roll-to-roll manufacturing of sheet components, and robotic assembly at the destination) can use all of those.
(1) Google earns $10,000 of profits per MWhr consumed for commodity data services; highly customized information services provided from and for 3 billion limitlessly-enabled new creatives in the developing world should be able to outperform Google's 60,000 employees (who generate profits approaching $1M per employee).