What is the optimum
shape for a thinsat?


Unlike the past 5 years of work,
it is a square.

Square thinsats are easier to make.

With gently curved folds,
thinsats are properly curved to
diperse opposite-side signal and
more stiffly resist vibration.

The depth of the curve should be
gentle, one or two wavelengths.



Mass M
Area A
Density M/A

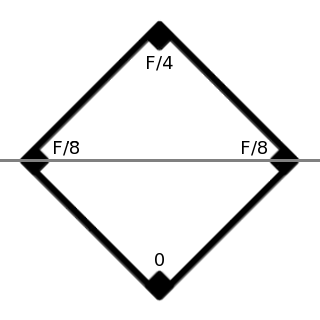
Triangle

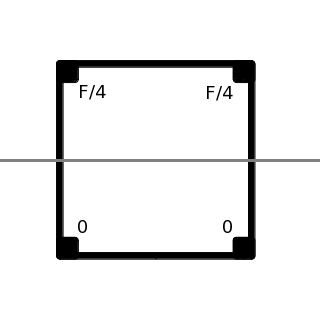
Square

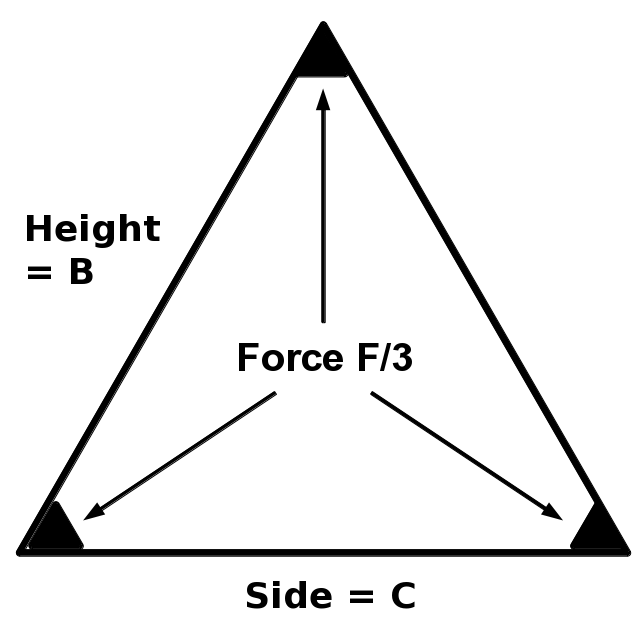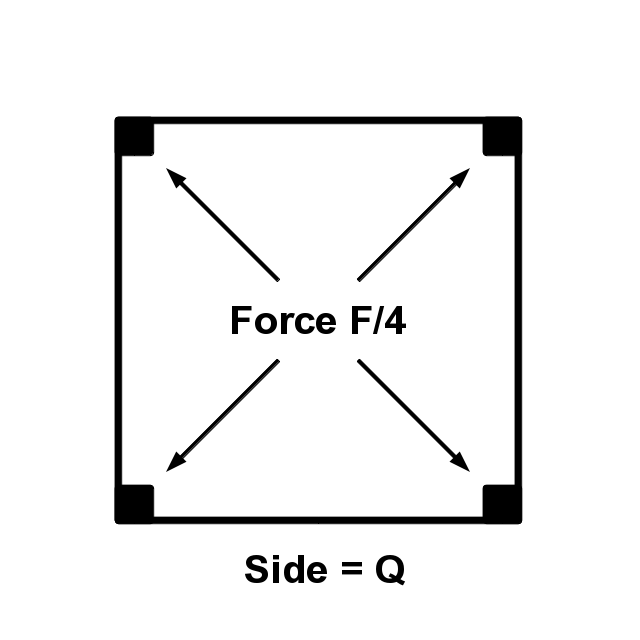Area

A = \sqrt{3} C^2 / 4 = B C / 2

A = Q^2

Side

C = 2 \sqrt{A / \sqrt{3} }

Q = \sqrt{A}

Height

B = (\sqrt{3}/2) C = \sqrt{\sqrt{3} ~ A}

Ratio

C = ( 2 /\sqrt[4]{3} ) Q ~ \approx ~ 1.51967 ~ Q

Q = ( \sqrt[4]{3}/2 ) C ~ \approx ~ 0.65804 ~ C

Rotational
Center

Average
Force F/2

I ~~ Moment
of Inertia

{ \Large { { 23 \sqrt{3} ~ M A } \over 486 } } ~\approx 0.081695 ~ M A

{ \Large { { M A } \over { 6 \sqrt{3} } } } ~\approx 0.096225 ~ M A

{\Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A

{ \Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A

T ~ ~ Torque

F \sqrt{\sqrt{3}~ A} / 6 ~\approx 0.21935 ~ F \sqrt{ A }

{ \Large { { F \sqrt{A} } \over { 3 \sqrt[4]{3} } } } ~\approx 0.25328 ~ F \sqrt{A}

0.25 ~ F \sqrt{A}

{ \Large { { F \sqrt{A} } \over { 4 \sqrt{2} } } } ~\approx 0.17678 ~ F \sqrt{A}

\dot \omega ~~ Angular
acceleration

{ \Large { { 81 F } \over { 23 \sqrt[4]{3} ~ M \sqrt{A} } } } ~\approx 2.0333 { \Large { F \over { M \sqrt{A} } } }

{ \Large { { 2 \sqrt[4]{3} ~ F } \over { M \sqrt{A} } } } ~\approx 2.6321 { \Large { F \over { M \sqrt{A} } } }

3.0 ~ { \Large { F \over { M \sqrt{ A } } } }

{ \Large { { 3 ~ F } \over { \sqrt{2} M \sqrt{A} } } } ~\approx 2.1213 { \Large { F \over { M \sqrt{A} } } }

\dot \omega ~~ Average

~\approx 2.3327 { \Large { F \over { M \sqrt{A} } } }

~\approx 2.5607 { \Large { F \over { M \sqrt{A} } } }

Notes:

The mass density per area is total mass M divided by the total area A for a thinsat.

To compute the moment of inertia I and the torque T :
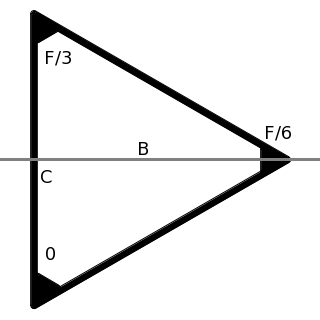
(1) find the pivot line - for an asymmetric figure like a triangle, it is where it would balance on a straight-edge. From the straight-edge at r = 0 , \int r ~ dm ~= \int W(r) r ~ dr ~= 0.
(2)The moment of inertia is the integral of the mass times the raidial distance squared, subject to (1): $ I = \int W(r) r^2 ~ dr
(3) The torque is the sum of the forces times their distance from the pivot line. For this exercise, we will treat the electrochromic thrusters as point forces in the corners, whose maximum force is the total force divided by the number of corners. "Neutral" is all the thrusters at half their maximum force, and the total force of all the thrusters at a given time should always sum to the neutral sum, half the total force.
Note, I am having trouble getting the same calculus results twice. Feel free to send corrections!

x = 3 y / B

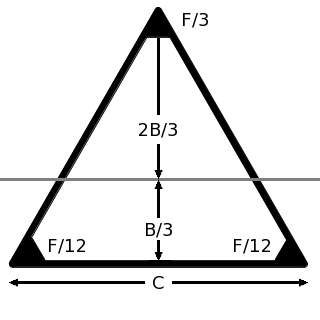
Balance: \int_{-B/3}^{2B/3}(2/3-y/B) y ~ dy ~= ( B^2 / 27 ) \int_{-1}^{2}(2-x) x ~ dx ~= ( B^2 / 27 ) ( (12-8)-(3+1) ) ~= 0
I ~= \int_{-B/3}^{2B/3}(M/A)C(2/3-y/B) y^2 ~ dy ~= { \large \left( { 2 M B^2 } \over 81 \right) } \int_{-1}^{2}(2-x)(x^2)~ dx ~= { \Large { { 23 \sqrt{3} ~ M A } \over 486 } } ~\approx 0.081695 ~ M A
T ~= ( F/3 ) ( 2B/3 ) - 2 ( F/12 )( 2B/3 ) ~= FB / 6 ~= F \sqrt{\sqrt{3} ~ A} / 6 ~\approx 0.21935 ~ F \sqrt{ A }
\dot \omega ~= T / I ~= { \Large { { 81 F } \over { 23 \sqrt[4]{3} ~ M \sqrt{A} } } } ~\approx 2.0333 { \Large { F \over { M \sqrt{A} } } }

symmetric! easier ...

x = 2 y / C

I ~= 2 \int_0^{C/2}(M/A)~B~(1 - 2y/C) y^2 ~ dy ~= { \Large { { B C^3 M } \over { 4 A } } } \int_0^{1}~(1 - x) x^2 ~ dx ~= { \Large { { M A } \over { 6 \sqrt{3} } } } ~\approx 0.096225 ~ M A
T ~= ( F / 3 )( C / 2 ) ~= { \Large { { F \sqrt{A} } \over { 3 \sqrt[4]{3} } } } ~\approx 0.25328 ~ F \sqrt{A}
\dot \omega ~= T / I ~= { \Large { { 2 \sqrt[4]{3} ~ F } \over { M \sqrt{A} } } } ~\approx 2.6321 { \Large { F \over { M \sqrt{A} } } }

I ~= 2 \int_0^{Q/2}(M Q / A) y^2 ~ dy ~= { \Large { { 2 ~ M Q^4 } \over { 24 ~ A } } } ~= { \Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A

T ~= 2 ( F / 4 ) ( Q / 2 ) ~= 0.25 ~ F \sqrt{A}

\dot \omega ~= T / I ~= 3.0 ~ { \Large { F \over { M \sqrt{ A } } } }

x = \sqrt{2} ~ y / Q

I ~= 2 \int_0^{Q/\sqrt{2}}(M/A)~\sqrt{2}~Q~(1 - \sqrt{2} ~ y /Q) y^2 ~ dy ~= { \Large { { M Q^4 } \over A } } \int_0^{1}~(1 - x) x^2 ~ dx ~= { \Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A
T ~= ( F / 4 )( Q / \sqrt{2} ) ~= { \Large { { F \sqrt{A} } \over { 4 \sqrt{2} } } } ~\approx 0.17678 ~ F \sqrt{A}
\dot \omega ~= T / I ~= { \Large { { 3 ~ F } \over { \sqrt{2} M \sqrt{A} } } } ~\approx 2.1213 { \Large { F \over { M \sqrt{A} } } }