|
Size: 6037
Comment:
|
Size: 6056
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
| ||<:-2>~+ What is the optimum<<BR>>shape for a thinsat?+~<<BR>><<BR>><<BR>>Unlike the past 5 years of work,<<BR>>~+it is a square.+~<<BR>><<BR>>Square thinsats are easier to make,<<BR>>and with gently curved folds,<<BR>>they are properly curved to diperse<<BR>> opposite-side signal and more<<BR>>stiffly resist vibration.<<BR>><<BR>>The depth of the curve should be<<BR>>gentle, one or two wavelengths.<<BR>><<BR>><<BR>><<BR>>Mass $M$<<BR>><<BR>>Density $M/A$||<:-3>{{attachment:SquareSat.png}}|| | ||<:-2>~+'''What is the optimum<<BR>>shape for a thinsat?'''+~<<BR>><<BR>><<BR>>Unlike the past 5 years of work,<<BR>>~+'''it is a square.'''+~<<BR>><<BR>>Square thinsats are easier to make,<<BR>>and with gently curved folds,<<BR>>they are properly curved to diperse<<BR>> opposite-side signal and more<<BR>>stiffly resist vibration.<<BR>><<BR>>The depth of the curve should be<<BR>>gentle, one or two wavelengths.<<BR>><<BR>><<BR>><<BR>>Mass $M$<<BR>>Area $A$<<BR>>Density $M/A$||<:-3>{{attachment:SquareSat.png}}|| |
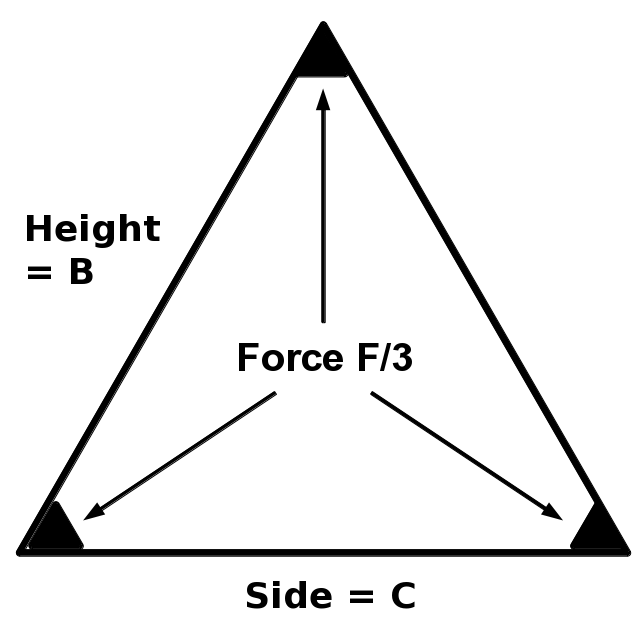
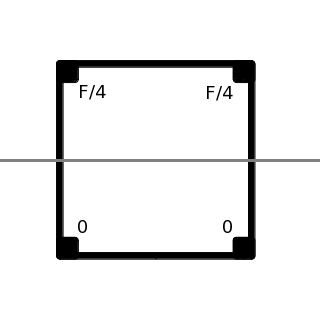
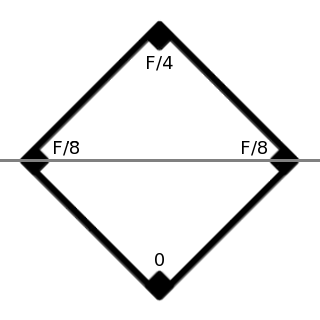
Triangle or Square?
What is the optimum |
|
|||
|
Triangle |
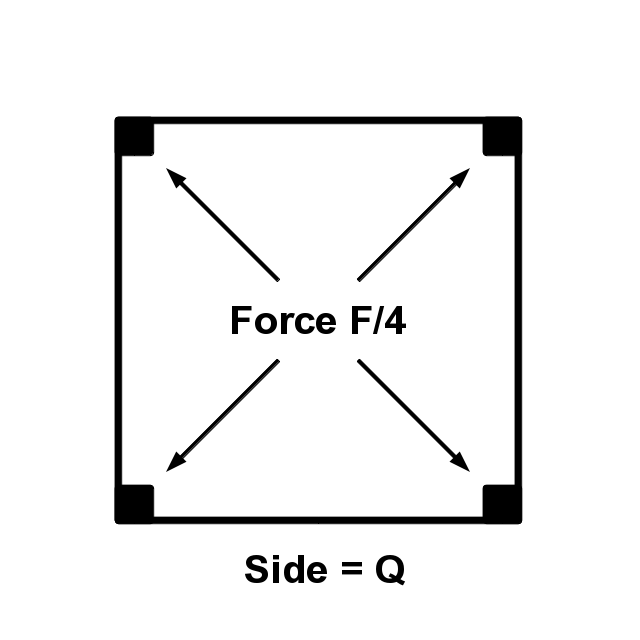
Square |
||
|
|
|
||
Area |
A = \sqrt{3} C^2 / 4 |
A = Q^2 |
||
Side |
C = 2 \sqrt{A / \sqrt{3} } |
Q = \sqrt{A} |
||
Height |
B = (\sqrt{3}/2) C = \sqrt{\sqrt{3} ~ A} |
|
||
Ratio |
C = ( 2 /\sqrt[4]{3} ) Q ~ \approx ~ 1.51967 ~ Q |
Q = ( \sqrt[4]{3}/2 ) C ~ \approx ~ 0.65804 ~ C |
||
Rotational |
|
|
|
|
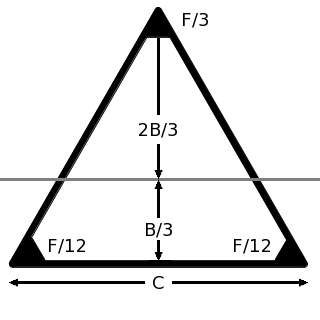
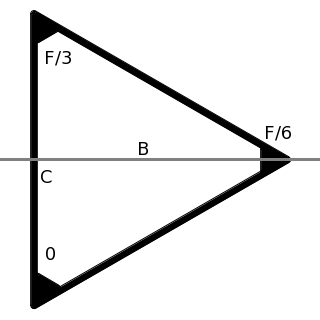
I ~~ Moment |
{ \Large { { 23 \sqrt{3} ~ M A } \over 486 } } ~\approx 0.081695 ~ M A |
{ \Large { { M A } \over { 6 \sqrt{3} } } } ~\approx 0.096225 ~ M A |
{\Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A |
{ \Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A |
T ~ ~ Torque |
F \sqrt{\sqrt{3}~ A} / 6 ~\approx 0.21935 ~ F \sqrt{ A } |
{ \Large { { F \sqrt{A} } \over { 3 \sqrt[4]{3} } } } ~\approx 0.25328 ~ F \sqrt{A} |
0.25 ~ F \sqrt{A} |
{ \Large { { F \sqrt{A} } \over { 4 \sqrt{2} } } } ~\approx 0.17678 ~ F \sqrt{A} |
\dot \omega ~~ Angular |
{ \Large { { 81 F } \over { 23 \sqrt[4]{3} ~ M \sqrt{A} } } } ~\approx 2.0333 { \Large { F \over { M \sqrt{A} } } } |
{ \Large { { 2 \sqrt[4]{3} ~ F } \over { M \sqrt{A} } } } ~\approx 2.6321 { \Large { F \over { M \sqrt{A} } } } |
3.0 ~ { \Large { F \over { M \sqrt{ A } } } } |
{ \Large { { 3 ~ F } \over { \sqrt{2} M \sqrt{A} } } } ~\approx 2.1213 { \Large { F \over { M \sqrt{A} } } } |
\dot \omega ~~ Average |
~\approx 2.3327 { \Large { F \over { M \sqrt{A} } } } |
~\approx 2.5607 { \Large { F \over { M \sqrt{A} } } } |
||
There is a 10% maneuvering advantage for the square, and certainly a manufacturing advantage. Time for a site redesign (sigh).
Notes: |
The mass density per area is total mass M divided by the total area A for a thinsat. |
|
x = 3 y / B |
|
symmetric! easier ... |
|
I ~= 2 \int_0^{Q/2}(M Q / A) y^2 ~ dy ~= { \Large { { 2 ~ M Q^4 } \over { 24 ~ A } } } ~= { \Large { { M A } \over 12 } } ~\approx 0.083333 ~ M A |
|
x = \sqrt{2} ~ y / Q |