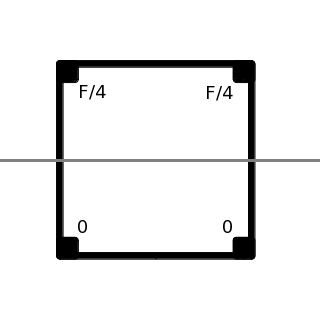
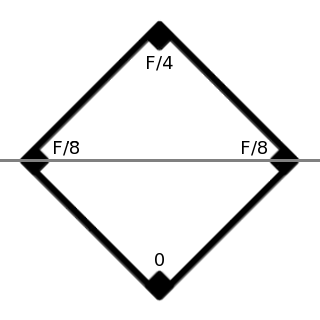
Triangle or Square?
What is the optimum shape for a thinsat?
Mass
|
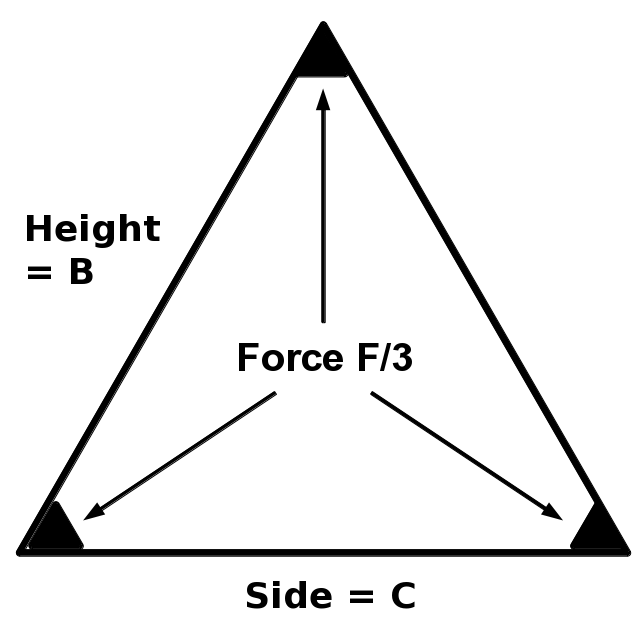
Triangle |
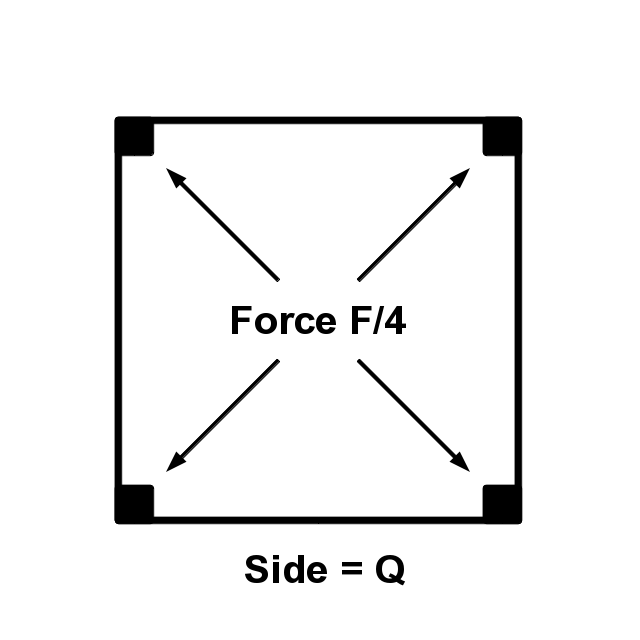
Square |
||
|
|
|
||
Area |
A = \sqrt{3} C^2 / 4 |
A = Q^2 |
||
Side |
C = 2 \sqrt{A / \sqrt{3} } |
Q = \sqrt{A} |
||
Height |
B = (\sqrt{3}/2) C = \sqrt{\sqrt{3} ~ A} |
|
||
Ratio |
C = ( 2 /\sqrt[4]{3} ) Q ~ \approx ~ 1.51967 ~ Q |
Q = ( \sqrt[4]{3}/2 ) C ~ \approx ~ 0.65804 ~ C |
||
Rotational |
|
|
|
|
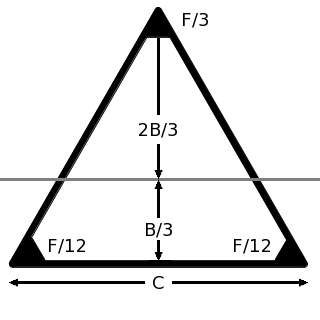
I ~~ Moment |
{ \Large { { 23 \sqrt{3} ~ M A } \over 486 } } ~\approx 0.081695 ~ M A |
{ \Large { { M A } \over { 6 \sqrt{3} } } } ~\approx 0.096225 ~ M A |
|
|
T ~ ~ Torque |
F \sqrt{\sqrt{3}~ A} / 6 ~\approx 0.21935 ~ F \sqrt{ A } |
{ \Large { { F \sqrt{A} } \over { 3 \sqrt[4]{3} } } } ~\approx 0.25328 ~ F \sqrt{A} |
|
|
\dot \omega ~~ Angular |
{ \Large { { 81 F } \over { 23 \sqrt[4]{3} ~ M \sqrt{A} } } } ~\approx 2.0333 { \Large { F \over { M \sqrt{A} } } } |
{ \Large { { 2 \sqrt[4]{3} ~ F } \over { M \sqrt{A} } } } ~\approx 2.6321 { \Large { F \over { M \sqrt{A} } } } |
|
|
Notes: |
The mass density per area is total mass M divided by the total area A for a thinsat. |
|
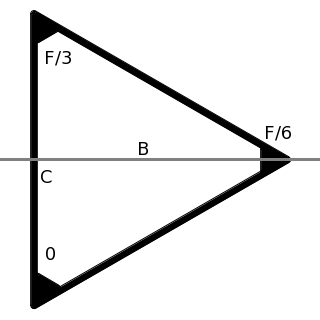
x = 3 y / B |
|
symmetric! easier ... |
|
|
|
|