Grating Lobes
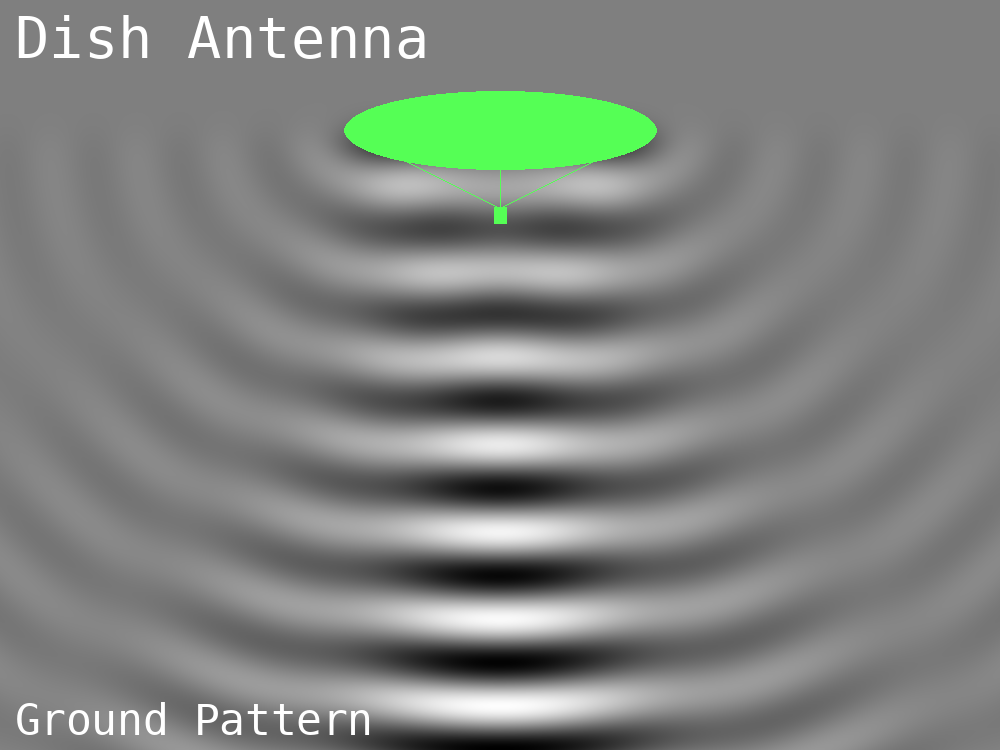
The first precision microwave radars used parabolic dishes to focus the beam. The waves from the transmitter source bounce off the parabolic dish reflector and reflect back into a narrow beam with a horizontal wavefront:
Look carefully at the waves around the edge. A parabolic antenna under uniform illumination leaks a little energy off to the side. These are called "side lobes".
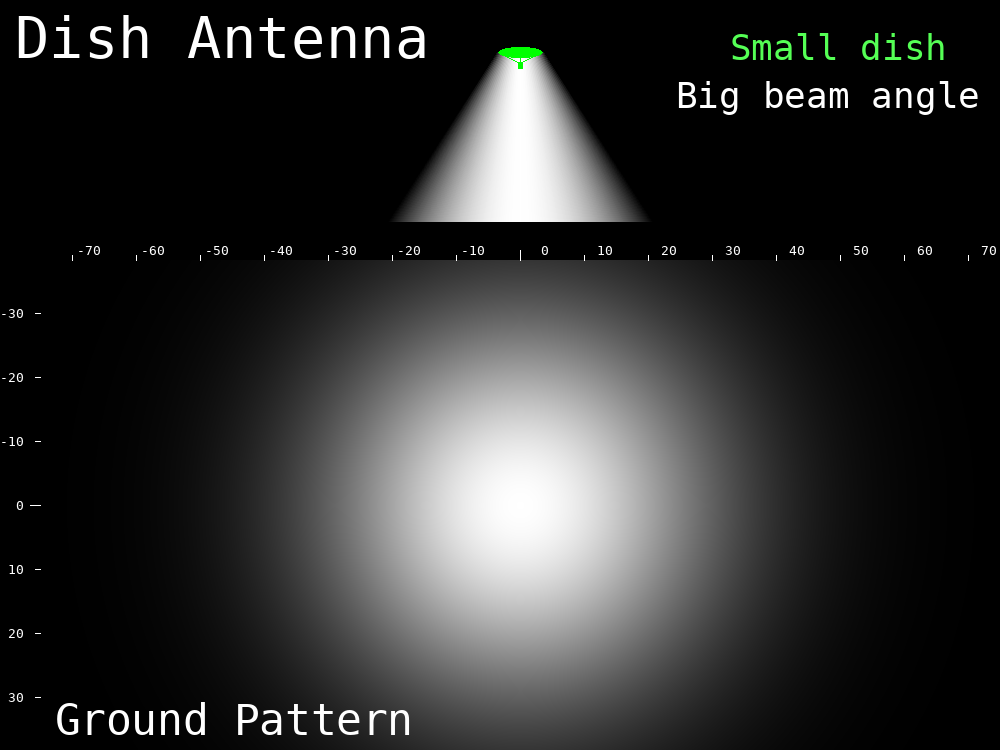
Because of the "diffraction limit", larger dishes produce narrower (smaller angle) beams than small dishes (with larger angle beams). The upper plot shows the dish changing size, the lower plot shows the size of a ground spot far below a larger or smaller orbiting dish:
Large dishes make smaller spots, but they are heavy. On the ground, they are distorted by weight and wind, and lose their shape. A parabolic dish is like a telescope mirror, it should keep its shape within a fraction of a wavelength or the distortions will spread the beam, making it fuzzy.
Also, big dishes take time to move around. Old style rotating dishes, and steered dishes, took many seconds to move from target to target. This was troublesome when detecting and tracking single airplanes; for ballistic missile early warning, a second is too long. As electronics became cheaper and budgets bigger, radars moved to a new system, phased array antennas.
Phased Arrays
Traditional phased arrays are two dimensional uniformly spaced grids of antennas in a flat plane. By changing the delays of the RF signal to from the antennas, the sum of the wavefronts from the antennas can be steered in different directions, electronically, very rapidly, while the planar antenna stays fixed.
Real phased arrays emit signals at angles to the perpendicular of the plane, but that is difficult to show on a two dimensional screen. So, I've made a slightly different kind of "two dimensional plane" phased array, so you can see how the transmitter antennas are phased to produce a beam. Server sky uses a three dimensional grid of thinsats to produce phased array beams, so this could be a slice of one of those arrays.
The individual antennas, shown here as little circles, are phased to emit signals that add up to a vertical downwards beam.
If you look carefully, you can see some sidelobe energy.
By phasing the antenna signals differently, you can steer the beam at a 30 degree angle. Switchover time can be very quick, moving from one beam to the other at the speed of light across the array.
The left side lobe is slightly more visible in this animation.
Server sky arrays are distorted by orbital mechanics; I call this Apogee Skew. This distorts the array into a rotating parallelipiped. This and the following plots show the ground illumination from a 5x5x5 three dimensional phased array. Typical arrays will range from 32x32x32 ( A 32768 thinsat, 98 kilogram array ) to 100 x 100 x 100 ( A 1 million thinsat, 3000 kg array ), but those would be much too large to illustrate here. The spacings between thinsats are on the order of meters, and increase for larger arrays, so they do not shade each other from the sun.
The illuminated parallelogram in the middle is the main lobe. It is surrounded by thousands of other spots. These are called grating lobes. Because the spacings are much larger than a wavelength, there are many angles at which the waves add together. Besides the energy focused on the very small main lobe, the vast majority of the energy is scattered into the other lobes.
The signals from all the thinsats, added together, are producing "nulls" in the pattern, black lines ("loci", the plural of locus) representing very little energy at those angles. Those null loci move as the array rotates around its orbital track (one rotation per orbit). Imagine that you are looking at the primary beam sweep along the equator, while the grating lobes create interference for other ground sites.
The size and spacing of the grating lobes are inversely proportional to the spacing of the thinsats:
If you add more thinsats, making the array bigger, the size of the grating lobes becomes smaller, but they do not vanish:
What's so BAD about grating lobes, anyway?
A very important point, however, is that even with grating lobes less total area is subjected to interference power as the array gets bigger. The power intensity at the center of the main focus is proportional to the square of the number of emitters at the same power - equivalently, to deliver the same power to the focus as one emitter, N emitters can each emit 1/N2 the amount of power, so the total off-axis power for the same received signal level goes down as 1/N.
There is nothing really destructive about grating lobes per se. Whether your array is compact and spreading unwanted power into a medium-sized spot and nowhere else, or it is spreading unwanted power into a large number of very small spots, every bit of power that does not land on the one small receive antenna the signal is intended for adds to the interference somewhere else. Given that people concentrate in villages and cities, it is almost certain that a medium sized spot will deliver unwanted power to neighbors, while grating lobes spots will probably deliver their unwanted power where nobody is listening anyway.
The array is moving and rotating, and because of its physical extent that changes the interference patterns. Consider a 98 kg array, with 32,768 thinsats in a 32x32x32 array with a fill factor of 0.01. The thinsat spacing is 8.8 meters and the array is 270 meters across. It turns 360 degrees or 2π radians in 4 hours (at M288) and the difference between the north and south array edge speeds is 120mm/sec - the array rotates almost 2 wavelengths in one 67 millisecond round trip ping time. This is phase compensated only for the main lobe. The grating lobes will not linger in one spot.
When there is interference, just retransmit, after changing spread-spectrum frequency bands. Chances are, the interferer will not be launching another packet at the next interference time. Also, the arrays move in orbit about 300 meters during one round trip ping time, so the geometry of the interferers will move them relative to the main focus. We have many tools at our disposal to punch packets through, and the collision tolerance of TCP/IP is one of them.
Randomization and spacing change
There is a very important trick we can play with server sky, which is more difficult with ground arrays: we can nonuniformly vary the position (and spacing) of the elements in the 3 dimensional array, and move them over time, perhaps by many wavelengths per minute. The results are spectacular:
The grating lobes are smeared out! They do not go away. The same amount of radio energy is splattered away from the main lobe, but it is not concentrated any more. That means it will not interfere nearly as much with ground receivers in other locations. Using time coded spread spectrum and signal correlation techniques, it is possible to send a detectable signal near the power noise floor. So until all the power from many different thinsat arrays, added together, exceeds the power of a main lobe, we can still punch a signal through. For a steady beam at one ground spot, the interferers will NOT be random, and evolve fairly slowly, given the 4 hour orbits; we can anticipate the interference, change signal amplitudes, and move nulls from array X over the ground spot of array Y. Or just try again; when an array redirects its packets at a different ground spot, the interferers shift, too.
The phasing of the transmitters gets a little more complicated, but not much - we are still doing a 12 digit accurate trigonometric calculation, but dependent on the individual position of each thinsat (in X, Y, and Z) relative to the target, as opposed to making some global calculation and spacing it out element by element.
This is a demonstration only. The actual spacing in deployed arrays will be dithered from an exact grid, but probably not randomly. Array position design will evolve towards smarter spacing functions, resulting in more closely packed non-shading arrays. See the page ArrayFill for a discussion.
Packet transmission and phasing
We must do some trigonometric calculations (probably a few "butterfly" sin/cos multiply-add phase rotations) per packet. If a large packet size is ten kilobytes, and the data rate is 1 gbit/second, then a packet (plus timing and framing) might need 100 microseconds to transmit. The array turns at 440 picoradians per microsecond, and at 1e7 meters and 45° surface angle the spot moves northwards at 6 millimeters per microsecond. As the array rotates and bends around the earth, the ground spot traverses east at 2.8 millimeters per microsecond. So in 100 microseconds the ground spot has moved less than 0.7 meters; we can recompute the focus for all the thinsats before we send the next packet towards that ground spot.
These calculations will be done with dedicated hardware, and require on the order of a nanojoule to compute, per packet, per thinsat (assuming precomputation and coefficients stored in RAM per ground spot). For smaller 500 byte packets, perhaps 10 launched in parallel simultaneously per array (total array transmit bit rate estimated at 10gb/sec and limited by intra-array communication) then we will be computing 20 million packet butterflies a second, 20 million nanojoules per second, or 20 milliwatts per thinsat. The intra-array bandwidth may improve, but we can expect Moore's law improvements for dedicated, localized, hardwired butterfly computation elements to improve faster. Please remember that these computational efficiencies are for dedicated hardware, and will be much lower for general purpose software-driven computation, which involves far more area, many more switching events, and multiple redundancy for radiation resistance.
A radiation pulse might scramble the pipeline values and phase for a single packet on one thinsat. The poorly timed packet from that one thinsat, out of a whole array, will have no significant impact on main lobe signal or side lobe noise power.
See-through antenna grids
One reason thinsat arrays are so sparse is that they must be widely spaced for illumination deep into the array. That spreads way too much power into sidelobes. However, with on-orbit assembly, we can imagine building extensions on the thinsats, long thin spars with antennas and perhaps even LNAs on them. These spars would be mostly optically transparent, but they would pass radio beams. Larger thinsats can also be assembled in orbit, but if they are too large they will turn too slowly, and will have difficult-to-correct vibration and flexing modes. Spar acoustic resonances will be difficult to compensate. These problems must be solved before we can deploy efficient SBSP transmitter arrays. Server Sky data communication does not need these improvements because it can be quite energy inefficient.
A note on the software libraries used - all these drawings and animations use libGD from the mate-ubuntu linux distribution; libGD seems broken in other distributions. apngasm converts directories of PNG single frames into APNG animations.