Deployment Orbits
here is a general discussion of orbits.
MoreLater - this needs more cleanup for version 3 thinsats.
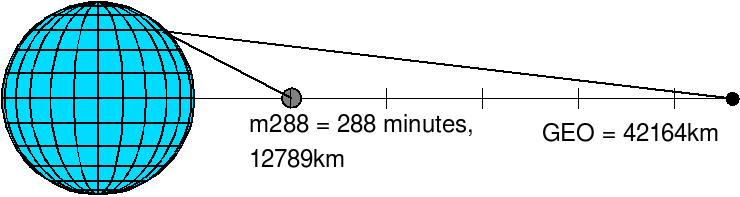
The first thinsat arrays will be deployed in a "4 hour" orbit, or more precisely a 14393.3 second orbit (sidereal). This means it passes over the same spot on earth 5 times per day ( = 6-1, the earth is turning underneath once per sidereal day ), for a repeat time relative to the ground of 288 minutes (which we will call an m288 orbit). A 4 hour equatorial circular orbit has a radius of 12789 kilometers, and an altitude above the equator of 6411 kilometers. This puts it in a "thinner" part of the Van Allen belt, with an estimated unshielded radiation dose of 1Mrad/year [citation needed].
Relative to a position on the earth, a thinsat will be visible in the same position 5 times per solar day, at intervals of 288 minutes. The constellation of associated orbits will therefore be called the m288 constellation. Of course, higher and lower orbit constellations are possible, though they will get more radiation. The m240 constellation will repeat 6 times per day, and the m360 constellation will repeat 4 times per day. For reasons that will become apparent, it is important that the orbital period is an integer fraction of a day.
The m288 central orbit can be seen at 58 degrees north and south latitude, at a distance of 10500 km. The round trip ping time is 70 milliseconds. The ground ping time through optical fiber across the United States is faster in theory, but ground networks are slowed by switches and indirect routes. Ping times from fat-pipe servers in Dallas Texas to mit.edu are 42 milliseconds , and to orst.edu are 49 milliseconds, so 70msec is not way out of line. However, much of the routing will travel "around the cloud", and without local caching in the "near" links, some pings may need as much as 200 milliseconds to hop from the far side of the orbit. Still, this is better than the 250+ millisecond ping time through a geosynchronous satellite.
Thinsats will actually be deployed in very slightly inclined and elliptical orbits, which map onto a nested set of tori ("torus-es") centered on the 4 hour, zero-inclination equatorial orbit. These are 4 hour orbits as well, and the largest tori are have major radii slightly offset inwards. A plane drawn perpendicularly to the center orbit (which intercepts the orbit in two places, and also intersects the center of the earth) will have "territories" marked on it for the regions around the various orbits, and the orbits passing through each "territory" can be treated as a property. This orbital property is further subdivided into angles around the orbit. Thinsats precisely positioned in each orbit will never intersect thinsats in other properties. Arrays in orbits in the same "property" will never intersect the orbits of arrays in different properties. This allows a large region of space to be filled with thinsats, potentially trillions of them. The density is limited by shading - at some point thinsats closer to the sun will reduce the daylight falling on the ones in the "back" of the orbit, and may begin to detectably reduce the sunlight falling on the earth.
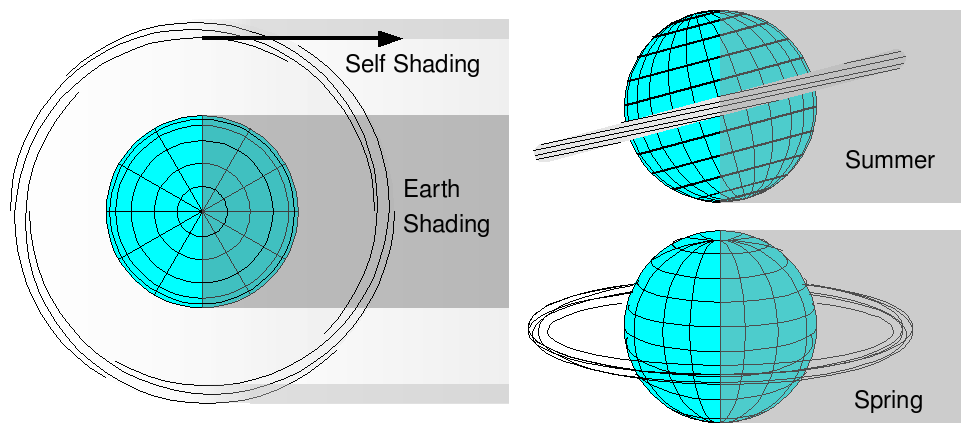
Shading
Thinsats will be spaced perhaps 50 meters apart in an array - an array with 32768 thinsats will be 1.6km on a side. This puts them far enough apart that the shade area behind one 20 centimeter diameter thinsat will never completely block sunlight to the thinsat behind it. If the nested tori extend outwards to 500 km around the central orbit, that is a spatial volume of 6E10 cubic kilometers. Potentially, that is room for 480 trillion thinsats at an average 50 meter spacing. This "fuzzy toroidal cloud" of thinsats will block some sunlight, both to the thinsats in the back of the toroidal cloud, and to the surface of the earth. With 40 trillion 300mm diameter thinsats, the light blockage to the ground would be about 14% at noontime near the equator, with the blockage zone following winter as shown above. The blockage of back thinsats near the sides of the orbit would be more severe - at the equinoxes, it could be as much as 95% for portions of a fully populated array. However, it is hard to imagine needing that many thinsats, even if they were operating mostly as space solar power satellites, beaming about 5 watts each to the ground, as that far exceeds the projected world demand for electricity. With a "mere" 10 trillion thinsats, the blockages would be 2% to the ground and 38% to the back of the array. Also, for power production (and one-way information broadcast) ping time is no longer an issue, so m360 and higher orbits can be used.
Shading and power beaming will be partly compensatory in the amount of energy beamed to earth. Part of the sun's energy will be blocked, cooling the earth. Part of the energy to a wider band will be delivered at somewhat low efficiency as electricity (and later heat) to the surface. The global effects can probably be balanced, although to second order the equator will be cooled a bit, and the highly populated electricity-using temperate zones will be warmed a bit. That will probably affect weather patterns if it is done at an enormous scale. The amounts of power involved to have a significant effect will probably be on the order of 200 Terawatts.
Nighttime Illumination
Thinsats will reflect some light. Oriented directly at the sun, most of the reflected light will go back to the sun, but some reflection will be diffuse and off angle. The sum of the diffuse reflected light from trillions of thinsats will appear as cloudy light in a band around the equator, interrupted by the Earth's shadow. At midnight on the equator, the illuminated bands will appear between the horizon (5.2 degrees wide) and 45 degrees from zenith (6.3 degrees wide). The two segments represent a total of 60 degrees of m288 orbital arc. The bands will be brightest just before the terminator, which will be slightly concave from the curvature of the earth's shadow.
How much light? For 30 trillion (5E13) thinsats, the total light will be about 2 times the total light from the full moon. The moon has an albedo of 0.12, and so it reflects about 1.5E15 watts of light into a solid angle of 2pi steradians. At 384000km away, we see about 1.6 milliwatts of light per meter2 ( approximately 0.3 lux). A thinsat will diffusely reflect perhaps 5% of the 33 watts of sunlight hitting it - 1.6 watts per thinsat. The visible 1/6 of 10 trillion thinsats would reflect perhaps 10 trillion watts of light, also into a solid angle of 2pi steradians. At an average of 10000 kilometers distance, the surface at the equator gets about 16 mW/m2, or approximately 3 lux. Since recommended office illumination is about 300 lux, that is way too much nighttime illumination!
Some diagrams showing the visible portions of server sky with flat orientation to the sun are shown here.
Without much better control of reflection, the total number of thinsats in at m288 will be limited by light pollution and its effects on nocturnal animals (some of whom may be sensitive to the monthly lunar illumination cycle, probably to a fraction of full moon light. This may limit the near-earth constellation to less than 1 trillion thinsats. However, by actively orienting thinsats so the reflection is directed away from the earth, and by reducing off-axis reflection (which is also good for thrust control), the amount of reflected light reaching the earth can be greatly reduced. This will need more study.
If 40 trillion thinsats are deployed as far out as the earth-moon L4 and L5 Lagrange points, the situation is much better. The constellations will be visible as often as the moon, though 60 degrees offset to east or west. On average, each constellation of 2E13 thinsats will be reflecting 3E13 watts, and at the same distance as the moon, each will appear to be about 2% of the brightness of the full moon, much less with reflectivity improvements and attitude control. If thinsats are deployed for large-scale power generation, where ping time is not important, farther out is better. However, two constellations at L5 and L4 will not be able to send power to the earth surface on the opposite side of the moon. A third constellation at the metastable L3 Lagrange point will also be needed to provide full ground coverage, and that will require constant station-keeping to stay in place.
Elevation above the horizon, interference with geosynchronous satellites
Assume that the first torus to be filled with arrays is at a minor radius of 200km from the central orbit. Refraction will lift the apparent elevation of the central orbit a few degrees above the horizon, so a south-facing antenna at 60 degrees north or south may be able to see the edges of the torus. However, ground sites further north or south of the central band may need to relay through other satellites, or through landlines on the ground. For latitudes between 10 degrees north or south, the torus will have similar ground antenna elevation angles as geosynchronous satellites. Assuming that the same satellite frequency bands are used for server sky as for existing geosynchronous services, latitudes between 10 degrees and 60 degrees north and 10 degrees and 60 degrees south should be able to make direct use of server sky.
Intentional gaps in the constellation
The orbits will not be completely filled - there will be large gaps in them to permit transit of launch vehicles. Establishing these "windows" will involve lots of negotiation, beyond the scope of this document.
If it ever proves practical to build space elevators, there will need to be other gaps in time and "property" so that the elevators and the thinsats never interact. A failing space elevator will collide with an undetermined number of thinsats (as well as destroying all the other space elevators), so space elevators and the permanent use of these orbits (or possibly any near-earth orbit) may prove incompatible.
In the short term, there will be millions, not trillions, of thinsats. They should still be assigned positions and orbits compatible with a much more crowded sky. It is good to know, going into this, that the region available for well behaved server sky orbits offers much room for growth.
Defining Property Within the m288 toroid
All server sky orbits in the m288 toroid will have the same identical semi-major axis, and hence the same identical 288 minute synoptic period, and the same 14393 second sidereal period. If the orbits are mapped correctly, every item in them will maintain the same approximate spacing to neighbors in three dimensions, even as the whole constellation makes one orbit around the earth and one "short axis rotation" around the central orbit. This allows very large numbers of thinsats to be deployed in the 60 billion cubic kilometers of server sky. Properties can be assigned much like IPV6 address space is assigned by ICANN - indeed, we may map IPV6 addresses onto particular orbital volumes, and know where in the sky a particular thinsat is from its IPV6 address, or vice versa. If we map down to one meter cubes, we will need about 65 bits of address space.
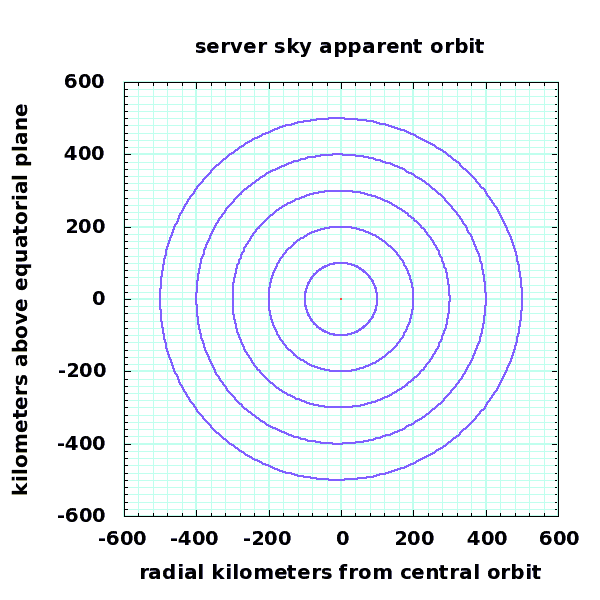
The space does not map in a rigidly cartesian way; the "toroids" we are mapping on are slightly distorted from perfectly circular minor cross sections, as shown:
|
500km cross section of nested torii around the m288, 12789km central orbit region. The outer orbits shown have an eccentricity of 0.039 and an inclination of 2.24 degrees. Although these torus cross sections look circular, they are actually distorted by as much as 3 kilometers from perfect circles. The outer torus has a volume of about 60 billion cubic kilometers. The inner torus, with a radius of 100km, has a volume of 2.5 billion cubic kilometers. |
|
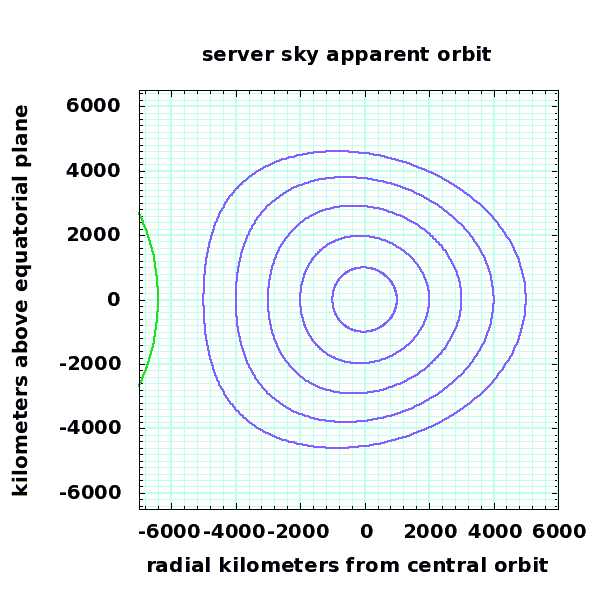
5000km cross section of nested torii around the m288, 12789km central orbit region. The outer orbits shown have an eccentricity of 0.39 and an inclination of 23 degrees. The edge of the earth is to the left. These unusually broad toruses demonstrate the distortion that occurs in outer orbits. The outer torus has a volume of about 6 trillion cubic kilometers (the earth is 1.09 trillion cubic kilometers), a perigee of 1411 kilometers altitude, and intercepts the orbits of many existing satellites and large debris objects, so such large torii should not actually be used. |
In addition, objects in the orbits will be advanced or delayed because of increased velocity at perigee and decreased velocity at apogee. This tends to spread objects near perigee (in the line of the orbit) by 1+eccentricity, and near apogee by 1-eccentricity. Thus, the volume elements will lengthen and shorten, and distort trapezoidally (proportional to the eccentricity, or the toroidal minor radius divided by the major radius) as they travel around the orbit. The arrays within those volumes will distort proportionally.
The below figure shows 3 orbits with 4 objects in each orbit, spaced at 0.25 times the period. The minor radius of the torus is greatly exaggerated.
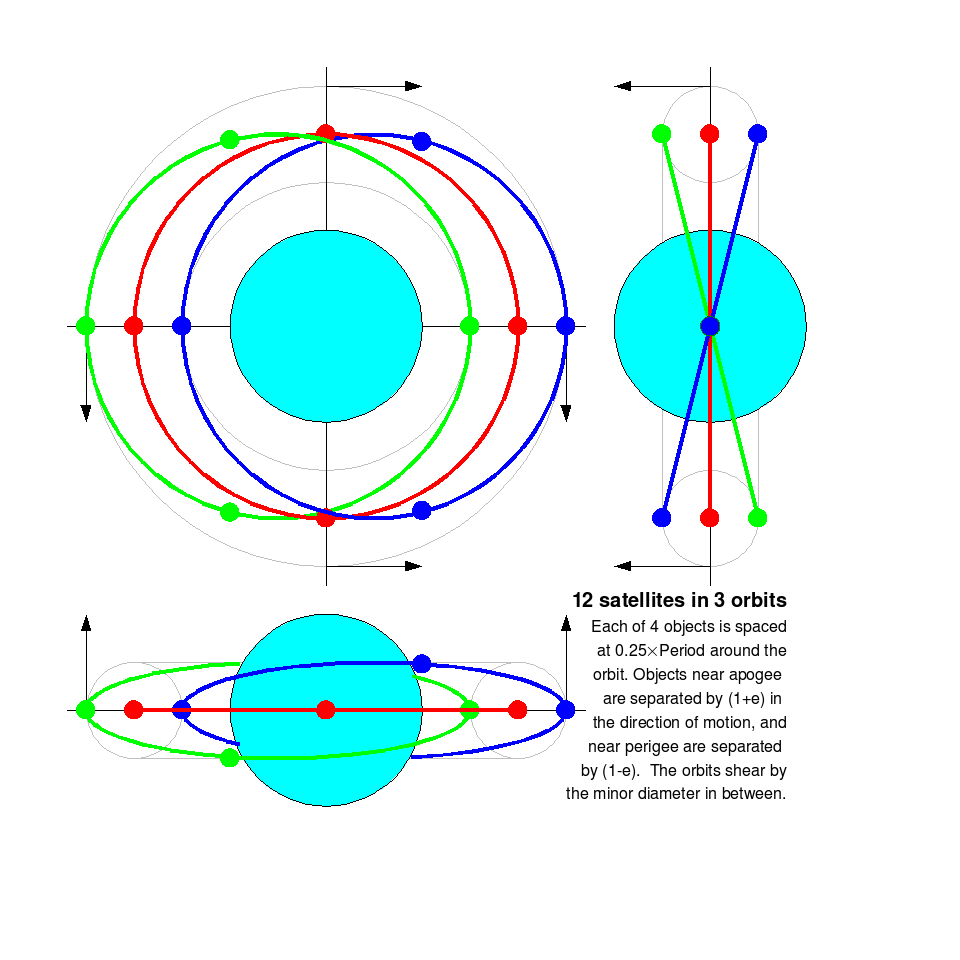
To fill a "torus" with a 3x3 square of orbits, add a rotated copy of the figure by 90 degrees, then rotate the pair by 45 degrees and expand the minor radius by sqrt(2). Then subtract the 3 duplicate central orbits. Repeat at larger spacings, add additional objects on each orbit, and the result is a filled torus (or whatever). This is based on a rectangular cartesian grid mapped into a circle at one angle from the equator to the fixed stars - the prime meridian seems like a good candidate. Other grids, such as triangular/hexagonal, can be mapped within the same circle (a cross-section of the largest torus).
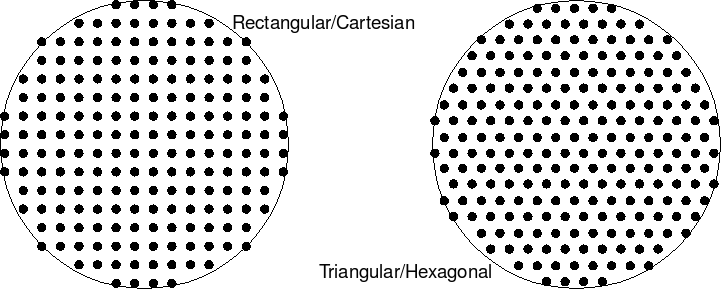
|
Assigning orbits within this map can be done many ways - by an organization like ICANN, perhaps working outwards from the center in the order of assignment. |
More about ToroidalOrbits .